一、二叉树介绍
简单地理解,满足以下两个条件的树就是二叉树:
-
本身是有序树;
-
树中包含的各个节点的度不能超过 2,即只能是 0、1 或者 2;
二、二叉树的性质
经过前人的总结,二叉树具有以下几个性质:
-
二叉树中,第 i 层最多有 2i-1 个结点。
-
如果二叉树的深度为 K,那么此二叉树最多有 2K-1 个结点。
-
二叉树中,终端结点数(叶子结点数)为 n0,度为 2 的结点数为 n2,则 n0=n2+1。
性质 3 的计算方法为:对于一个二叉树来说,除了度为 0 的叶子结点和度为 2 的结点,剩下的就是度为 1 的结点(设为 n1),那么总结点 n=n0+n1+n2。同时,对于每一个结点来说都是由其父结点分支表示的,假设树中分枝数为 B,那么总结点数 n=B+1。而分枝数是可以通过 n1 和 n2 表示的,即 B=n1+2*n2。所以,n 用另外一种方式表示为 n=n1+2*n2+1。
两种方式得到的 n 值组成一个方程组,就可以得出 n0=n2+1。
二叉树还可以继续分类,衍生出满二叉树和完全二叉树。
三、满二叉树
如果二叉树中除了叶子结点,每个结点的度都为 2,则此二叉树称为满二叉树。

如图 2 所示就是一棵满二叉树。
满二叉树除了满足普通二叉树的性质,还具有以下性质:
-
满二叉树中第 i 层的节点数为 2n-1 个。
-
深度为 k 的满二叉树必有 2k-1 个节点 ,叶子数为 2k-1。
-
满二叉树中不存在度为 1 的节点,每一个分支点中都两棵深度相同的子树,且叶子节点都在最底层。
-
具有 n 个节点的满二叉树的深度为 log2(n+1)。
四、完全二叉树
如果二叉树中除去最后一层节点为满二叉树,且最后一层的结点依次从左到右分布,则此二叉树被称为完全二叉树。
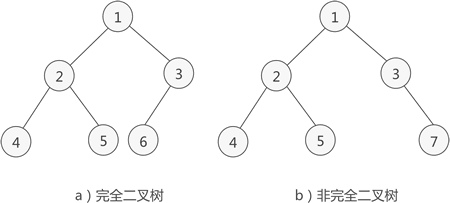
如图 3a) 所示是一棵完全二叉树,图 3b) 由于最后一层的节点没有按照从左向右分布,因此只能算作是普通的二叉树。
完全二叉树除了具有普通二叉树的性质,它自身也具有一些独特的性质,比如说,n 个结点的完全二叉树的深度为 ⌊log2n⌋+1。
⌊log2n⌋ 表示取小于 log2n 的最大整数。例如,⌊log24⌋ = 2,而 ⌊log25⌋ 结果也是 2。
对于任意一个完全二叉树来说,如果将含有的结点按照层次从左到右依次标号(如图 3a)),对于任意一个结点 i ,完全二叉树还有以下几个结论成立:
-
当 i>1 时,父亲结点为结点 [i/2] 。(i=1 时,表示的是根结点,无父亲结点)
-
如果 2*i>n(总结点的个数) ,则结点 i 肯定没有左孩子(为叶子结点);否则其左孩子是结点 2*i 。
-
如果 2*i+1>n ,则结点 i 肯定没有右孩子;否则右孩子是结点 2*i+1 。
五、树的存储结构
二叉树的存储结构有两种,分别为顺序存储和链式存储。
1 、顺序存储
二叉树的顺序存储,指的是使用顺序表(数组)存储二叉树。需要注意的是,顺序存储只适用于完全二叉树。换句话说,只有完全二叉树才可以使用顺序表存储。因此,如果我们想顺序存储普通二叉树,需要提前将普通二叉树转化为完全二叉树。
有读者会说,满二叉树也可以使用顺序存储。要知道,满二叉树也是完全二叉树,因为它满足完全二叉树的所有特征。
普通二叉树转完全二叉树的方法很简单,只需给二叉树额外添加一些节点,将其"拼凑"成完全二叉树即可。如图 1 所示:
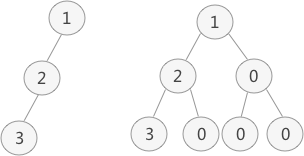
图 1 中,左侧是普通二叉树,右侧是转化后的完全(满)二叉树。
解决了二叉树的转化问题,接下来学习如何顺序存储完全(满)二叉树。
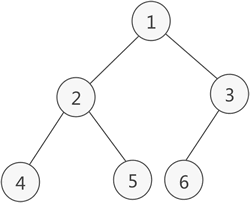
完全二叉树的顺序存储,仅需从根节点开始,按照层次依次将树中节点存储到数组即可。
 --->
---> 
存储由普通二叉树转化来的完全二叉树也是如此
 --->
---> 
非常重要
完全二叉树具有这样的性质,将树中节点按照层次并从左到右依次标号(0,1,2,3,...),
若节点 i 有左右孩子,则其左孩子节点为 2 * i + 1,右孩子节点为 2 * i+2。
此性质可用于还原数组中存储的完全二叉树
2、链式存储
 --->
---> 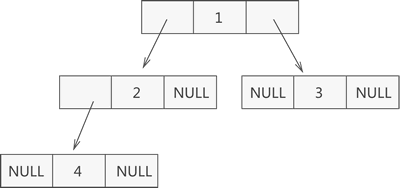
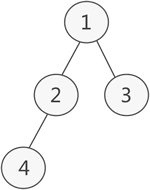
如图 1 所示,此为一棵普通的二叉树,若将其采用链式存储,则只需从树的根节点开始,将各个节点及其左右孩子使用链表存储即可。
因此,图 1 对应的链式存储结构如图 2 所示:
由图 2 可知,采用链式存储二叉树时,其节点结构由 3 部分构成(如图 3 所示):
-
指向左孩子节点的指针(Lchild);
-
节点存储的数据(data);
-
指向右孩子节点的指针(Rchild)

六、树的遍历
-
前序遍历: 先输出父节点, 再遍历左子树和右子树
-
中序遍历: 先遍历左子树, 再输出父节点, 再遍历右子树
-
后序遍历: 先遍历左子树, 再遍历右子树, 最后输出父节点
看输出父节点的顺序,就确定是前序,中序还是后序
示例代码如下:

1 public class BinaryTree { 2 3 4 public static void main(String[] args) { 5 BinaryTree binaryTree = new BinaryTree(); 6 TreeNode node = binaryTree.initTree(); 7 List<Integer> preList = binaryTree.preOrder(node); 8 System.out.println("preList = " + preList); 9 List<Integer> midOrder = binaryTree.midOrder(node); 10 System.out.println("midOrder = " + midOrder); 11 List<Integer> afterOrder = binaryTree.afterOrder(node); 12 System.out.println("afterOrder = " + afterOrder); 13 } 14 15 // 先遍历左子树,再遍历右子树,最后输出父节点 16 public List<Integer> afterOrder(TreeNode node) { 17 List<Integer> list = new ArrayList<>(); 18 if (node != null) { 19 list.addAll(afterOrder(node.left)); 20 list.addAll(afterOrder(node.right)); 21 list.add(node.val); 22 } 23 return list; 24 } 25 26 // 先遍历左子树,再输出父节点,再遍历右子树 27 public List<Integer> midOrder(TreeNode node) { 28 List<Integer> list = new ArrayList<>(); 29 if (node != null) { 30 list.addAll(midOrder(node.left)); 31 list.add(node.val); 32 list.addAll(midOrder(node.right)); 33 } 34 return list; 35 } 36 37 // 先输出父节点,再遍历左子树和右子树 38 public List<Integer> preOrder(TreeNode node) { 39 List<Integer> list = new ArrayList<>(); 40 if (node != null) { 41 list.add(node.val); 42 list.addAll(preOrder(node.left)); 43 list.addAll(preOrder(node.right)); 44 } 45 return list; 46 } 47 48 private TreeNode initTree() { 49 // 1 50 // 2 3 51 // 4 5 6 7 52 TreeNode node2 = new TreeNode(2, new TreeNode(4), new TreeNode(5)); 53 TreeNode node3 = new TreeNode(3, new TreeNode(6), new TreeNode(7)); 54 return new TreeNode(1, node2, node3); 55 } 56 57 58 static class TreeNode { 59 int val; 60 TreeNode left; 61 TreeNode right; 62 63 TreeNode() { 64 } 65 66 TreeNode(int val) { 67 this.val = val; 68 } 69 70 TreeNode(int val, TreeNode left, TreeNode right) { 71 this.val = val; 72 this.left = left; 73 this.right = right; 74 } 75 } 76 }
顺序存储二叉树的遍历
示例代码如下:

1 public class ArrBinaryTree { 2 3 public List<Integer> preOrder(int[] arr) { 4 return preOrder(arr, 0); 5 } 6 7 // 前序遍历 8 private List<Integer> preOrder(int[] arr, int index) { 9 List<Integer> list = new ArrayList<>(); 10 if(index < arr.length) { 11 list.add(arr[index]); 12 list.addAll(preOrder(arr, 2 * index + 1)); 13 list.addAll(preOrder(arr, 2 * index + 2)); 14 } 15 return list; 16 } 17 18 public List<Integer> midOrder(int[] arr) { 19 return midOrder(arr, 0); 20 } 21 22 // 中序遍历 23 private List<Integer> midOrder(int[] arr, int index) { 24 List<Integer> list = new ArrayList<>(); 25 if(index < arr.length) { 26 list.addAll(midOrder(arr, 2 * index + 1)); 27 list.add(arr[index]); 28 list.addAll(midOrder(arr, 2 * index + 2)); 29 } 30 return list; 31 } 32 33 // 前序遍历转化 34 public TreeNode preOrderConvert(int[] arr) { 35 return preOrderConvert(arr, 0); 36 } 37 38 private TreeNode preOrderConvert(int[] arr, int index) { 39 if(index < arr.length) { 40 TreeNode treeNode = new TreeNode(arr[index]); 41 treeNode.left = preOrderConvert(arr, 2 * index + 1); 42 treeNode.right = preOrderConvert(arr, 2 * index + 2); 43 return treeNode; 44 } 45 return null; 46 } 47 48 public static void main(String[] args) { 49 int[] arr = {1, 2, 3, 4, 5, 6, 7}; 50 ArrBinaryTree arrBinaryTree = new ArrBinaryTree(); 51 // 前序遍历 52 List<Integer> proList = arrBinaryTree.preOrder(arr); 53 System.out.println("proList = " + proList); 54 // 中序遍历 55 List<Integer> midList = arrBinaryTree.midOrder(arr); 56 System.out.println("midList = " + midList); 57 58 // 转化成树,前序遍历转化 59 TreeNode treeNode = arrBinaryTree.preOrderConvert(arr); 60 System.out.println("treeNode = " + treeNode); 61 } 62 63 static class TreeNode { 64 int val; 65 TreeNode left; 66 TreeNode right; 67 68 TreeNode() { 69 } 70 71 TreeNode(int val) { 72 this.val = val; 73 } 74 75 TreeNode(int val, TreeNode left, TreeNode right) { 76 this.val = val; 77 this.left = left; 78 this.right = right; 79 } 80 } 81 }
七、线索化二叉树
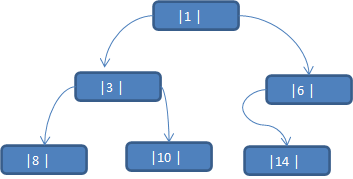
将数列 {1, 3, 6, 8, 10, 14 } 构建成一颗二叉树,当我们对这颗二叉树进行中序遍历时, 输出数列为 {8, 3, 10, 1, 6, 14 }
但是 6, 8, 10, 14 这几个节点的左右指针,并没有完全的利用上,如果我们希望充分的利用 各个节点的左右指针, 让各个节点可以指向自己的前后节点,怎么办?
解决方案:线索二叉树
线索二叉树基本介绍
-
n 个结点的二叉链表中含有 n+1 【公式 2n-(n-1)=n+1】 个空指针域。 利用二叉链表中的空指针域, 存放指向该结点在某种遍历次序下的前驱和后继结点的指针(这种附加的指针称为"线索")
-
这种加上了线索的二叉链表称为线索链表, 相应的二叉树称为线索二叉树(Threaded BinaryTree)。
-
根据线索性质的不同, 线索二叉树可分为前序线索二叉树、 中序线索二叉树和后序线索二叉树三种
-
前驱结点和后继节点:
- 一个结点的前一个结点, 称为前驱结点
- 一个结点的后一个结点, 称为后继结点
-
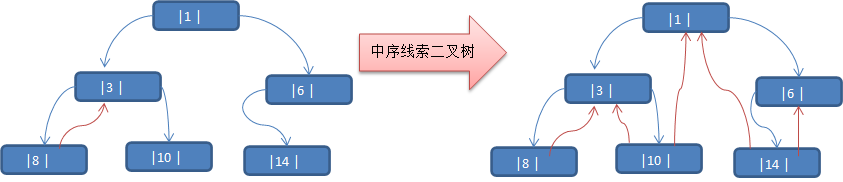
当我们对二叉树进行中序遍历时, 得到的数列为 {8, 3, 10, 1, 6, 14 }
-
那么 8 节点的前驱结点为 null ,8 和后驱节点为 3
-
那么 3 节点的前驱结点为 8 ,3 和后驱节点为 10
-
以此类推…
-
代码实现

1 public class ThreadBinaryTree { 2 3 // 最后处理过的节点,即当前处理节点的前一个处理节点 4 private TreeNode preNode; 5 6 // 中序线索化 7 public void midOrderThreadedNodes(TreeNode node) { 8 if (node != null) { 9 // 1、先线索化左子树 10 midOrderThreadedNodes(node.left); 11 // 2、线索化当前节点 12 if (node.left == null) { 13 node.leftType = 1; 14 node.left = preNode; 15 } 16 if (preNode != null && preNode.right == null) { 17 preNode.rightType = 1; 18 preNode.right = node; 19 } 20 // 更新preNode节点 21 preNode = node; 22 // 3、再线索化右子树 23 midOrderThreadedNodes(node.right); 24 } 25 } 26 27 // 遍历中序线索化二叉树 28 public List<Integer> midOrderThreadList(TreeNode treeNode) { 29 List<Integer> list = new ArrayList<>(); 30 // 找到leftType = 1 && left == null 的节点 31 // 这个节点就是第一个线索化的节点 32 TreeNode node = treeNode; 33 while (node != null) { 34 35 while (node.leftType == 0) { 36 node = node.left; 37 } 38 39 list.add(node.val); 40 41 while (node.rightType == 1) { 42 node = node.right; 43 list.add(node.val); 44 } 45 46 node = node.right; 47 } 48 return list; 49 } 50 51 public List<Integer> midOrder(TreeNode node) { 52 List<Integer> list = new ArrayList<>(); 53 if (node != null) { 54 list.addAll(midOrder(node.left)); 55 list.add(node.val); 56 list.addAll(midOrder(node.right)); 57 } 58 return list; 59 } 60 61 public static void main(String[] args) { 62 ThreadBinaryTree threadBinaryTree = new ThreadBinaryTree(); 63 TreeNode treeNode = threadBinaryTree.initTree(); 64 List<Integer> midOrder = threadBinaryTree.midOrder(treeNode); 65 System.out.println("midOrder = " + midOrder); 66 67 threadBinaryTree.midOrderThreadedNodes(treeNode); 68 System.out.println("treeNode = " + treeNode); 69 70 List<Integer> orderThreadList = threadBinaryTree.midOrderThreadList(treeNode); 71 System.out.println("orderThreadList = " + orderThreadList); 72 } 73 74 private TreeNode initTree() { 75 // 1 76 // 2 3 77 // 4 5 6 78 TreeNode node2 = new TreeNode(2, new TreeNode(4), new TreeNode(5)); 79 TreeNode node3 = new TreeNode(3, new TreeNode(6), null); 80 return new TreeNode(1, node2, node3); 81 } 82 83 84 static class TreeNode { 85 int val; 86 // 左指针类型,0树节点指向类型 1线索化指针,前驱节点 87 int leftType; 88 TreeNode left; 89 // 右 指针类型,0树节点指向类型 1线索化指针,后驱节点 90 int rightType; 91 TreeNode right; 92 93 TreeNode() { 94 } 95 96 TreeNode(int val) { 97 this.val = val; 98 } 99 100 TreeNode(int val, TreeNode left, TreeNode right) { 101 this.val = val; 102 this.left = left; 103 this.right = right; 104 } 105 } 106 }
参考:http://data.biancheng.net/view/194.html




 浙公网安备 33010602011771号
浙公网安备 33010602011771号