CART剪枝过程
Classification And Regression Tree,CART,分类与回归树,一种二叉决策树。作为一种决策树算法,CART与其他决策树一样,由特征选择、树的生成和剪枝组成。本文介绍CART算法生成决策树 后如何对其进行剪枝(将子树变成叶子节点)。
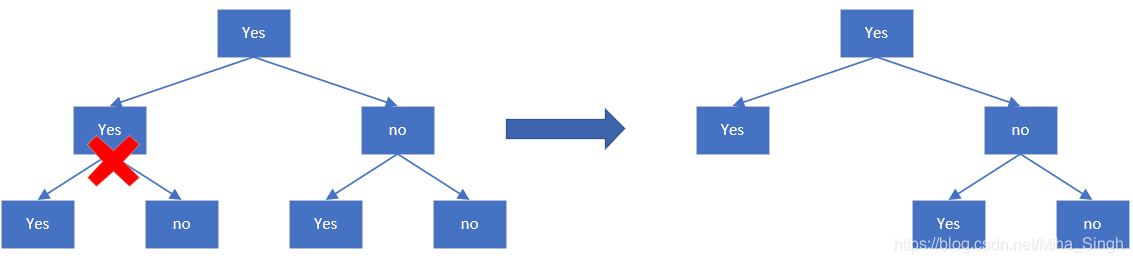
剪枝过程分为两步:
- 从的底端开始不断剪枝,直到的根节点,形成一个子树序列
- 通过交叉验证选择最优的子树作为剪枝后的CART
1. 剪枝,形成子树序列
在剪枝过程中,使用以下损失函数作为是否剪枝的依据:
其中可以是任意子树,是在训练数据上的误差(根据回归或者分类,可以是均方误差或者基尼指数),是的叶子节点数,是参数,是参数是时的整体损失。可以权衡训练数据的拟合程度与模型复杂度()。因此,越大,则更倾向于选择更小的树,随着的增大,使最小的树逐渐从变成最后的单节点的树。
对于固定的,可以验证存在唯一的子树使最小。
具体过程如下:
从开始,自下而上地考虑每个内部节点,考虑两种情况:
- 1)以为根节点的子树,其损失为:;
- 2)对进行剪枝,即将作为叶子节点,其损失为:;
我们来比较,看看要不要对进行剪枝:
- 当较小时,可以容忍模型有较高的复杂度,这个时候主要保证在训练数据上误差很小即可,所以,即这个时候不需要剪枝;
- 当逐渐增大到某一值时,这个时候需要考虑在训练数据上误差很小且模型有较低的复杂度,所以,即这个时候剪不剪枝都可以;
- 当继续增大,,这个时候剪枝带来的收益大于作为一棵子树所带来的收益,所以要剪枝;
从以上过程我们可以看出,对于树中的每个内部节点,都有一个特定的阈值,来决定是否需要对其进行剪枝,且该阈值等于(由上述关于大小的比较可以得出)。其实 可以看作是模型性能和复杂度之间的一个权衡, 的分子是剪枝后误差的增大量(相当于精度的下降量),分母是剪掉的叶子结点数,相当于在模型复杂度方面的收益, 是二者的一个比值,即愿意精度降低和复杂度降低之间的一个权衡。
因此,在生成时,我们可以计算的每个内部节点的,选择其中最小的最为 (为啥要选择最小的呢?这个还不是很清楚),对该结点进行剪枝后就可以子树序列中的了。接着在的基础上持续剪枝,就可以得到最终的子树序列。
在生成子树序列的过程中,我们也可以得到一个序列,这个序列对应着一个区间,这与我们得到的子树序列是相对应的,对应着。
其实,在生成子树序列的过程中,我们计算是为了判断:当模型复杂度有多重要时我们需要对进行剪枝,也就是剪枝后带来的收益大于作为子树带来的模型效果收益。
2. 交叉验证
使用验证数据集,测试子树序列中每棵子树的损失,选择最小的作为剪枝后的决策树,这个时候也对应了一个。
Reference
- 统计学习方法,李航,第二版



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个奇形怪状的面试题:Bean中的CHM要不要加volatile?
· [.NET]调用本地 Deepseek 模型
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· .NET Core 托管堆内存泄露/CPU异常的常见思路
· PostgreSQL 和 SQL Server 在统计信息维护中的关键差异
· DeepSeek “源神”启动!「GitHub 热点速览」
· 我与微信审核的“相爱相杀”看个人小程序副业
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· C# 集成 DeepSeek 模型实现 AI 私有化(本地部署与 API 调用教程)
· spring官宣接入deepseek,真的太香了~