【剑指Offer】59、按之字形顺序打印二叉树

  题目描述：

  请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

  解题思路：

  这道题仍然是二叉树的遍历，相当于层次遍历，可以和第22题：从上往下打印二叉树 和第60题：把二叉树打印成多行 这几个题对比起来进行分析。

  相对而言，本题按之字形顺序打印二叉树是比较复杂的，短时间内不太好分析得到结论，可以通过具体的实例来进行分析，从具体的例子得出普遍的结论。

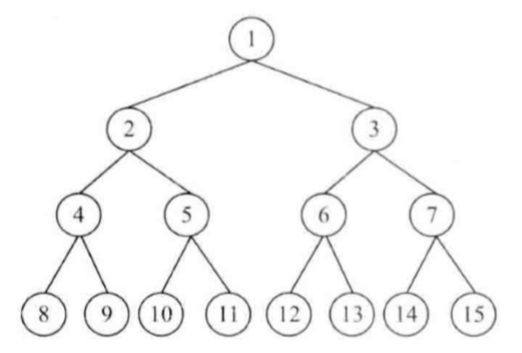
  实际上，层次遍历我们都是借助一定的数据容器来实现的，比如按行打印使用的是队列。在本题，我们使用的是栈，具体分析如下：我们可以设置两个辅助栈，在打印某一层的结点时，将下一层的子结点保存到相应的栈里；如果当前打印的是奇数层（第一层、第三层等），则先保存左子节点再保存右子结点到第一个栈中，如果当前打印的是偶数层（第二层、第四层等），则先保存右子结点再保存左子结点到第二个栈中。

  举例：

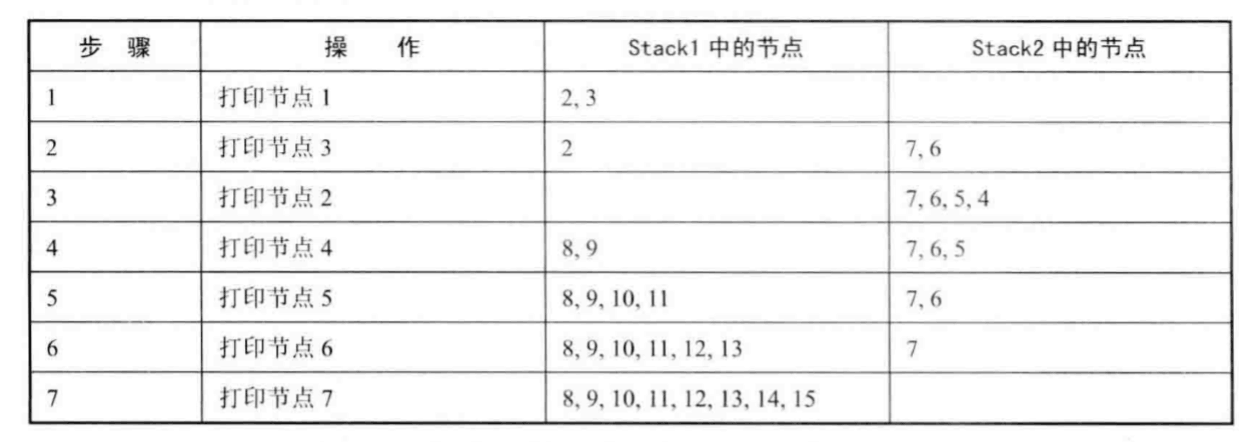
  编程实现（Java）：

import java.util.ArrayList;
import java.util.Stack;
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;
    }
}
public class Solution {
    public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        /*
        思路：之字形打印，用两个栈来实现
        打印奇数行时，将他的左右节点保存到另一个栈中，先左后右
        打印偶数行时，同样将左右节点保存到栈中，先右后左
        */
        ArrayList<ArrayList<Integer>> res=new ArrayList<>();
        if(pRoot==null)
            return res;
        Stack[] stack=new Stack[2]; //stack[0]保存偶数层，stack[1]保存奇数层,注意java不支持泛型数组
        stack[0]=new Stack();
        stack[1]=new Stack();
        TreeNode root=pRoot;
        stack[1].push(root);
        int num=1; //当前打印的是第几层
        while((!stack[0].isEmpty())||(!stack[1].isEmpty())){ //有一个栈不为空
            int flag=num%2; //当前要打印的栈
            //int save=flag==0?1:0; //下一层保存在这个栈中
            ArrayList<Integer> row=new ArrayList<>();
            while(!stack[flag].isEmpty()){
                TreeNode temp=(TreeNode)stack[flag].pop();
                if(flag==1) { //当前是奇数行
                    if(temp.left!=null)
                        stack[0].push(temp.left);
                    if(temp.right!=null)
                        stack[0].push(temp.right);
                }else{ //当前是偶数行
                    if(temp.right!=null)
                        stack[1].push(temp.right);
                    if(temp.left!=null)
                        stack[1].push(temp.left);
                }
                row.add(temp.val);
            }
            res.add(row);
            num++;
        } 
        return res;
     }

}

  或者可以下面这种写法更好理解一下：

public class Solution {
   public ArrayList<ArrayList<Integer> > Print(TreeNode pRoot) {
        //之字形顺序打印二叉树
        ArrayList<ArrayList<Integer>> res=new ArrayList<>();
        if(pRoot==null)
            return res;
        Stack<TreeNode> stack1=new Stack<>();
        Stack<TreeNode> stack2=new Stack<>();
        stack1.push(pRoot);
        while(!stack1.isEmpty() || !stack2.isEmpty()){
            ArrayList<Integer> list=new ArrayList<>();
            if(!stack1.isEmpty()){
                while(!stack1.isEmpty()){
                    TreeNode temp=stack1.pop();
                    list.add(temp.val);
                    if(temp.left!=null)  //先左后右
                        stack2.push(temp.left);
                    if(temp.right!=null)
                        stack2.push(temp.right);
                }
            }else{
                while(!stack2.isEmpty()){
                    TreeNode temp=stack2.pop();
                    list.add(temp.val);
                    if(temp.right!=null)   //先右后左
                        stack1.push(temp.right);
                    if(temp.left!=null)
                        stack1.push(temp.left);
                }
            }
            res.add(list);
        }
        return res;
    }
}