【剑指Offer】58、对称的二叉树

  题目描述：

  请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

  解题思路：

  本题判断一棵树是不是对称的，和第18题可以对比分析：二叉树的镜像，和LeetCode第101题：101. 对称二叉树是同一道题。

  解法一：递归法

  《剑指Offer》中给出的解答是定义一种先遍历右子结点，再遍历左子结点的新遍历方法，称为前序遍历的对称遍历，实际上，我们不用这样，可以直接找到对称二叉树的规律：

  对称二叉树满足：根结点的左右子树相同，左子树的左子树和右子树的右子树相同，左子树的右子树和右子树的左子树相同即可。

  根据以上规律，直接使用递归便可以写出对应的代码，并不难理解，可以结合以下几个实例进行分析。

  解法二：迭代法（广度优先遍历）

  广度优先遍历的一般做法是借助队列，这里我们可以在初始化时把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

  这一方法的关键是队列中出队列的两个连续的结点就应当是对称树中相等的结点。

  举例：

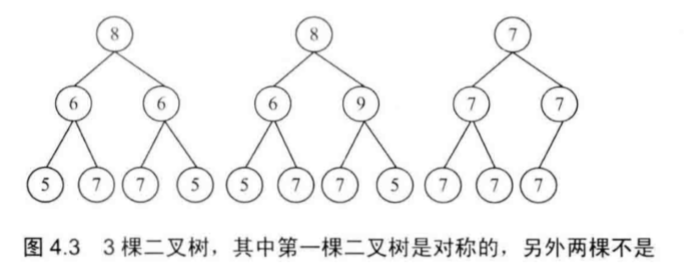
  编程实现（Java）：

//解法一：递归法，时间复杂度O(n),空间复杂度O(n)
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;
    }
}
public class Solution {
    boolean isSymmetrical(TreeNode pRoot){
        //左的左，和右的右进行比较，左的右和右的左比较
        if(pRoot==null)
            return true;
        return isSymmetrical(pRoot.left,pRoot.right);
    }
    boolean isSymmetrical(TreeNode pleft,TreeNode pright){
        if(pleft==null && pright==null)
            return true;
        if(pleft==null || pright==null)
            return false;
        if(pleft.val!=pright.val)
            return false;
        return isSymmetrical(pleft.left,pright.right) && isSymmetrical(pleft.right,pright.left);
    }
}

//解法二：迭代法（广度优先遍历）时间复杂度O(n),空间复杂度O(n)
class Solution {
    public boolean isSymmetric(TreeNode root) {
        Queue<TreeNode> queue=new LinkedList<>();
        queue.add(root);
        queue.add(root);

        while(!queue.isEmpty()){
            TreeNode t1=queue.poll();
            TreeNode t2=queue.poll();
            if(t1==null && t2==null)
                continue;
            if(t1==null || t2==null)
                return false;
            if(t1.val!=t2.val)
                return false;
            
            queue.add(t1.left);
            queue.add(t2.right);
            queue.add(t1.right);
            queue.add(t2.left);
        }
        return true;
    }
}