【剑指Offer】55、链表中环的入口结点
题目描述:
给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
解题思路:
本题是一个比较典型的链表题目,难度适中。首先,对于大多人来说,看到这道题是比较开心的,因为判断一个链表是否存在环的方法,基本上大家都知道,就是快慢指针法,但是再仔细一看,本题除了判断是否有环之外,还要找到这个环的入口点,这就略有些复杂了。
具体思路如下:
第一步:确定一个链表是否有环。这一步就是快慢指针法,定义两个指针,同时从链表的头结点出发,快指针一次走两步,慢指针一次走一步。如若有环,两个指针必定相遇,也就是如果快指针反追上了慢指针,说明存在环(这里要注意,两指针相遇的地方一定在环中,但不一定是环的入口),如果快指针走到了链表的末尾(指向了NULL),则说明不存在环。
第二步:找到环的入口点。这还是可以利用双指针来解决,两个指针初始都指向头结点,如果我们可以知道环中的结点个数,假设为n,那么第一个指针先向前走n步,然后两个指针(另一个从头结点开始)同时向前,当两个指针再次相遇时,他们的相遇点正好就是环的入口点。
这其实并不难理解,假设链表中共有m个结点,环中有n个结点,那么除环以外的结点数就是m-n,第一个指针先走了n步,然后两个指针一起向前,当他们一起向前m-n步时,第一个链表正好走完一遍链表,返回到环的入口,而另一个指针走了m-n步,也正好是到了环的入口。
现在,我们还有一个关键的问题:如何知道链表中的环包含了几个结点呢?也就是,怎么求这个n。
实际上这也不难,在第一步中,我们提到:快慢指针相遇的地方一定在环中,并且通过第一步我们已经找到了这个位置,接下来,只要从这个相遇的结点出发,一边移动一边计数,当它绕着环走一圈,再次回到这个结点时,就可以得到环中的结点数目n了。
举例:
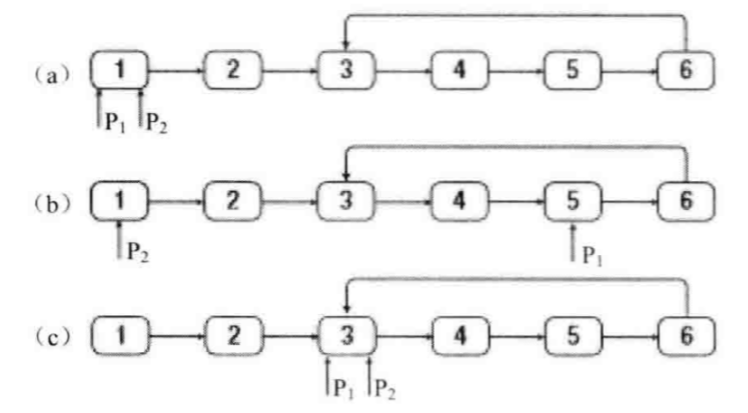
编程实现(Java):
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
public class Solution {
public ListNode EntryNodeOfLoop(ListNode pHead){
if(pHead==null||pHead.next==null)
return null;
ListNode meet=meetingNode(pHead); //相遇的节点
if(meet==null)
return null;
//求环的长度
ListNode temp=meet;
int len=1;
temp=temp.next;
while(temp!=meet){
temp=temp.next;
len++;
}
ListNode fast=pHead,slow=pHead;
//快指针先走len步
for(int i=0;i<len;i++)
fast=fast.next;
while(slow!=fast){
slow=slow.next;
fast=fast.next;
}
return slow;
}
//判断是否有环,返回相遇的节点,思路:快慢指针,若有环必相遇
public ListNode meetingNode(ListNode pHead){
if(pHead==null||pHead.next==null)
return null;
ListNode fast=pHead,slow=pHead;
while(fast.next!=null){
slow=slow.next;
fast=fast.next.next;
if(slow==fast)
return slow;
}
return null;
}
}
通过查看相关文章发现,实际上,当找到在环中相遇的结点meetingNode时,一个指针指向meetingNode,另一个指针指向head,然后一起向前,这两个指针相遇的位置就一定是环的入口点,这个证明比较复杂,但实际上这和先走n步的解法本质上还是一样的,只不过是在环里面多绕几圈。可以参考一下 https://zhuanlan.zhihu.com/p/85349101 的证明过程。
public class Solution {
public ListNode EntryNodeOfLoop(ListNode pHead) {
//链表中环的入口结点
if(pHead==null)
return null;
ListNode meetingNode=hasCycle(pHead);
if(meetingNode==null) //不存在环
return null;
ListNode head=pHead;
while(head!=meetingNode){
head=head.next;
meetingNode=meetingNode.next;
}
return head;
}
public ListNode hasCycle(ListNode pHead){
//判断是否有环,快慢指针法
if(pHead==null || pHead.next==null)
return null;
ListNode slow=pHead,fast=pHead;
while(fast!=null && fast.next!=null){
slow=slow.next;
fast=fast.next.next;
if(slow==fast)
return slow;
}
return null;
}
}



