【剑指Offer】35、数组中的逆序对

  题目描述：

  在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007。

  输入描述：

  题目保证输入的数组中没有的相同的数字数据范围：

• 对于%50的数据,size<=10^4
• 对于%75的数据,size<=10^5
• 对于%100的数据,size<=2*10^5

  解题思路：

  本题一个最容易想到的解法是暴力解法，顺序扫描整个数组，每扫描到一个数字时，逐个比较该数字与后面的数字的大小关系，统计逆序对的个数，假设数组中有n个数字，则每个数字都要和O(n)个数字做比较，因此，这个暴力解法的时间复杂度为O(n^2)。

  一般情况下，最容易想到的往往不是最优解法。在这里，我们采用分治的思想，类比归并排序算法来分析此题。

  首先将数组分隔成子数组，统计出子数组内部逆序对数目，然后再统计相邻子数组之间的逆序对数目，统计过程中还需要对数组进行排序，这实际上就是归并排序的过程。主要考虑的是合并两个有序序列时，计算逆序对数。对于两个有序升序序列，设置两个下标分别指向开始位置，每次比较两个指针对应的值，如果第一个序列当前值大于第二个序列当前值，则有第一个序列“当前长度”个逆序对。

  这看起来好像比较拗口，但是从代码中可以直观看出。

  举例：

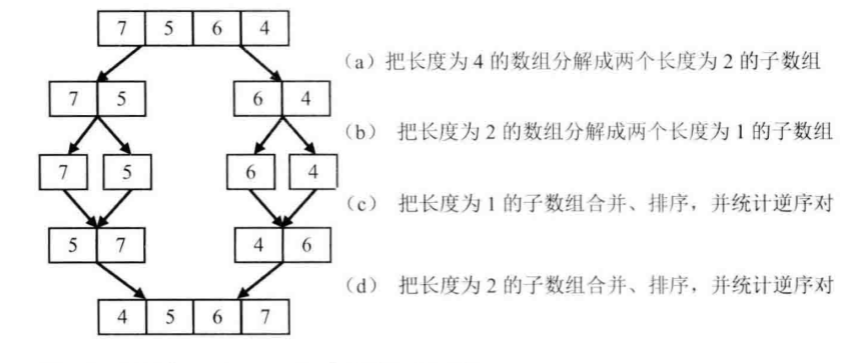
  编程实现（Java）：

public class Solution {
    int res=0;
    public int InversePairs(int [] array) {
        //数组中的逆序对，归并排序
        if(array==null || array.length==0)
            return 0;
        findInversePairs(array,0,array.length-1);
        return res%1000000007;
    }
    public void findInversePairs(int[] array,int low,int high){
        if(low<high){
            int mid=low+(high-low)/2;
            findInversePairs(array,low,mid); //左一半递归
            findInversePairs(array,mid+1,high); //右一半递归
            //merge
            merge(array,low,mid,high);
        }
    }
    public void merge(int[] array,int low,int mid,int high){
        int i=low,j=mid+1;
        int[] temp=new int[high-low+1];
        int k=0;
        while(i<=mid && j<=high){
            if(array[i]<=array[j])
                temp[k++]=array[i++];
            else {   //大于，说明是逆序
                temp[k++] = array[j++];
                res += (mid - i + 1);
                res = res%1000000007;
            }
        }
        while(i<=mid)
            temp[k++]=array[i++];
        while(j<=high)
            temp[k++]=array[j++];

        for(i=0;i<temp.length;i++)
            array[low+i]=temp[i];
    }
}