【剑指Offer】26、二叉搜索树与双向链表
题目描述:
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
解题思路:
首先要理解此题目的含义,在双向链表中,每个结点都有前后两个指针;二叉树中,每个结点都有两个指向子结点的左右指针,同时,二叉搜索树树也是一种排序的数据结构。因此,从结构上看,双向链表的前后指针和二叉搜索树的左右指针结构相似,因此,可以实现互相之间的转换。
首先,根据二叉搜索树的特点,左结点的值<根结点的值<右结点的值,据此不难发现,使用二叉树的中序遍历得到的数据序列就是递增的排序顺序。因此,首先确定应该采用中序遍历方法。
接下来,可以根据下图,将树分为三个部分,值为10的根结点、根为6的左子树和根为14的右子树。不难看出以下规律:根据中序遍历的顺序,当我们遍历到根结点时,它的左子树已经转换为一个排好序的双向链表,并且链表最后一个结点是左子树值最大的结点,我们把这个值最大(8)的结点同根结点链接起来,10就成了最后一个结点,接着遍历右子树,将根结点同右子树中最小的结点链接起来。
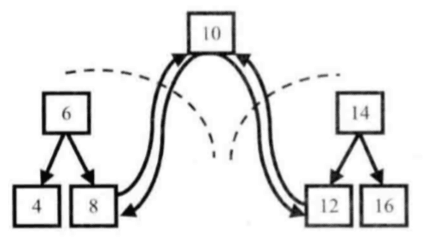
很明显,左右子树具有和原问题相同的结构,因此直接利用递归即可实现。
举例:
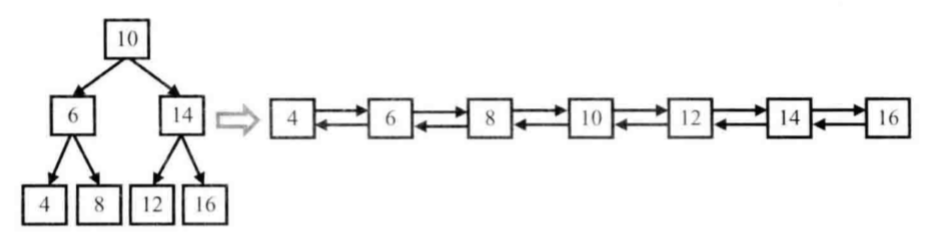
编程实现(Java):
public class Solution {
public TreeNode Convert(TreeNode pRootOfTree) {
//根据中序遍历采用递归依次实现
if(pRootOfTree==null)
return null;
TreeNode curEndoflink=null;
TreeNode root=pRootOfTree;
Convert(root,curEndoflink);
while(pRootOfTree!=null && pRootOfTree.left!=null){ //链表头是最左边
pRootOfTree=pRootOfTree.left;
}
return pRootOfTree;
}
//curEndoflink保存的是当前已经排好的链表的最后一个节点
public TreeNode Convert(TreeNode pRootOfTree,TreeNode curEndoflink){
if(pRootOfTree==null)
return null;
TreeNode root=pRootOfTree;
if(root.left!=null) //将左子树构建为链表
curEndoflink=Convert(root.left,curEndoflink);
//将根接在左子树的链表之后
root.left=curEndoflink;
if(curEndoflink!=null)
curEndoflink.right=root;
curEndoflink=root; //引用改变值,需要return
if(root.right!=null) //将右子树构建为链表
curEndoflink=Convert(root.right,curEndoflink);
return curEndoflink;
}
}
博学 审问 慎思 明辨 笃行



