【笔记】点分治
(文章中的图使用 \(\text{CS Academy}\) 制作)
前置知识:树的重心
定义
- 树的重心是树的一个节点,其所有的子树中最大的子树节点数最少 .
图示
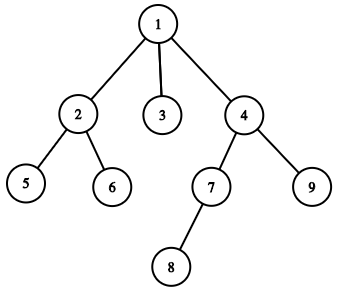
如图,这是一棵树,这棵树的重心就是 \(1\) 号节点,它的最大子树节点数为 \(4\) .
性质
树的重心有如下一些性质:
- 树中所有点到某个点的距离和中,到重心的距离和是最小的,如果有两个距离和,他们的距离和一样。
- 把两棵树通过一条边相连,新的树的重心在原来两棵树重心的连线上。
- 一棵树添加或者删除一个节点,树的重心最多只移动一条边的位置。
- 一棵树最多有两个重心,且相邻。
求解
那怎么求重心呢?下面提供一种思路:选择一个节点作为根,设 \(siz_i\) 表示以 \(i\) 为根的树的总节点个数,则 \(siz_i=\sum siz_{j\in son_x} +1\)。只需在 \(\text{dfs}\) 过程中找到最大的子树节点,并与其上方的节点数做比较,就可以找出树的重心了。代码如下(使用链式前向星存图):
void dfs(int x, int fa) {
f[x] = 0; siz[x] = 1;
for(int i = head[x]; i; i = edge[i].next) {
int y = eg[i].to;
if(y == fa) continue;
dfs(y, x);
siz[x] += siz[y];
f[x] = max(f[x], siz[y]);
}
f[x] = max(f[x], n - siz[x]);
if(f[x] < ans) {
ans = f[x];
root = x;
}
}
例题
点分治
题目描述
给定一个有 \(n\) 个点的树,询问树上距离为 \(k\) 的点对是否存在。
解题思路
首先考虑暴力的做法,过程大概是这样子的:
- 处理经过当前根节点的路径
- 删掉根节点
- 对生成的每棵子树的根节点重复步骤 \(1、2\)
对于一个满二叉树来说,时间复杂度是 \(O(\log n)\) 的,但是对于一条链,时间复杂度就大大增加了,是 \(O(n)\) 的 。
考虑怎么优化,对于任意一棵树,可以以它的重心为根,再进行上面的三步操作,就能很好的保证时间复杂度是 \(O(\log n)\) 的,于是刚刚的步骤就变成了:
- 找到当前树的重心,以重心为根节点
- 处理经过当前根节点的路径
- 删掉根节点
- 对生成的每棵子树的根节点重复步骤 \(1、2、3\)
找重心前面已经讲了,那怎么处理经过当前根节点的路径呢?
显然,对于任意一条经过根节点的路径,有 \(dis_{u,v}=dis_{u,root}+dis_{root,v}\) ,所以我们可以处理出每一个节点到根节点的距离,并且记录到 \(dis\) 数组里,一个简单的 \(\text{dfs}\) 就可以完成。
所以,对于任意一个询问 \(k\) ,只要有任意两个不在同一子树的 \(\text{dis}\) 能组合出 \(k\) ,那就说明长度为 \(k\) 的路径是存在的。
为什么不能在同一子树里呢?
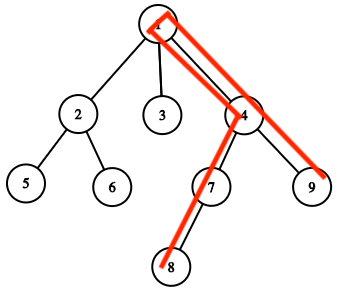
仍然看这张图,如果要求的是 \(dis_{8,9}\) ,这种情况下 \(dis_{1,4}\) 会被算两遍,是不合法的,所以只能在相异的两个子树中。
我们可以建立一个 \(\text{bool}\) 数组 \(\text{judge}\) ,对于每个合法的 \(\text{dis}\) ,把 \(judge_{dis}\) 的值置为 \(true\) ,然后对于每一个询问 \(\text{k}\) ,遍历所有的 \(\text{dis}\) ,若 \(judge_{k-dis}=true\) ,则说明长度为 \(k\) 的路径是存在的。代码如下:
inline void solve(int t) {
int i, j;
vis[t] = judge[0] = 1; calc(t);
for(i = head[t]; i; i = edge[i].next) {
j = edge[i].to;
if(vis[j]) continue;
tot = siz[j];
f[root = 0] = n;
dfs(j,0);//找重心
solve(root);
}
} //不断递归找每个子树的重心
inline void getdis(int t, int fa) {
tmp[++tmp[0]] = dis[t];
int i, j, k;
for(i = head[t]; i; i = edge[i].next) {
j = e[i].to, k = e[i].dis;
if(vis[j] || j == fa) continue; //vis和fa限制了这个子树只能向下遍历。
dis[j] = dis[t] + k;
getdis(j, t);
}
}//递归求每个点到根节点的距离
inline void calc(int t) {
int p = 0, i, j, k, l;
for(i = head[t]; i; i = edge[i].next) {
j = edge[i].to, k = edge[i].dis;
if(vis[j]) continue;
tmp[0] = 0; dis[j] = k;
getdis(j, t);
for(k = tmp[0]; k; k --)
for(l = 1; l <= m; l ++)
if(query[l] >= tmp[k])
ans[l] |= judge[query[l] - tmp[k]];
for(k = tmp[0]; k; k --)
q[++ p] = tmp[k], judge[tmp[k]] = true;
}
for(i = p; i; i --)
judge[q[i]] = 0;
}
时间复杂度
最多分 \(\log n\) 层,每层都是 \(n\) 级别的,所以点分治的时间复杂度是 \(O(n\log n)\) 的。



