PointNet论文理解和代码分析(详解)
简介
3D展示有以下几种常见情况:
- multi-view images(多视角的图片)+2D CNN:图片表示3D数据存在失真。
- vulmetric data(3D体素)+3D CNN:voxel的分辨率太小,不同物体区别不大,分辨率太高,复杂度太高。
- mesh data+GNN:图卷积神经网络处理网格数据。
- image depth+ CNN:带有深度的图片信息
- point cloud +DL:点云数据运用深度学习的方法

点云数据优势:
- 原始数据
- 包含\((x,y,z),RGB,normal\)等信息
- 比较好描述3D形状
论文的Abstract中介绍到,点云是一种重要的几何数据结构。不同于以往的研究,作者设计了一种新型直接处理点云的神经网络结构PointNet。PointNet能提供统一的结构在分类,语义分割等应用上。
介绍
输入为三通道点云数据,\((x,y,z)\),输出整体的类别或者每个点所处的部分或者每个点的类别。对于目标分类任务,输出为\(k\)个分数,实现\(k\)分类。对于语义分割任务,输出\(n*m\)个分数,分别对应\(n\)个点相对于\(m\)类别的分数。
点云特征:
无序性:虽然输入的点云是有顺序的,但是显然这个顺序不应当影响结果。所以PointNet使用了对称函数,类型\(max(x_1, x_2 ....x_n)函数\),不管怎么变化\(x_i\)的位置,函数结果都是不变的。
点之间的交互:每个点不是独立的,而是与其周围的一些点共同蕴含了一些信息,Pointnet分类网络并没有考虑很多点的周围信息,当然卷积本来就是操作邻域的,分类网络提取的是一组全局feature,语义分割考虑了每个点的特征。
变换不变性:比如点云整体的旋转和平移不应该影响它的分类或者分割结果,对于这个特征,PointNet首先对输入点集做了一个输入变换,变化到一个规范空间。mlp之后又做了一个特征变换。
空间变换网络--spatial transform network
CNN分类时,通常需要考虑输入样本的局部性、平移不变性、缩小不变性,旋转不变性等,以提高分类的准确度。这些不变性的本质就是图像处理的经典方法,即图像的裁剪、平移、缩放、旋转,而这些方法实际上就是对图像进行空间坐标变换,我们所熟悉的一种空间变换就是仿射变换,就类似计算机图形学中学习到的三维坐标变换,使用矩阵乘法。
空间变换网络,实际上是在神经网络的某两层之间引入一个空间变换网络,这个网络的参数也是需要学习得,该空间变换网络包括两个部分。
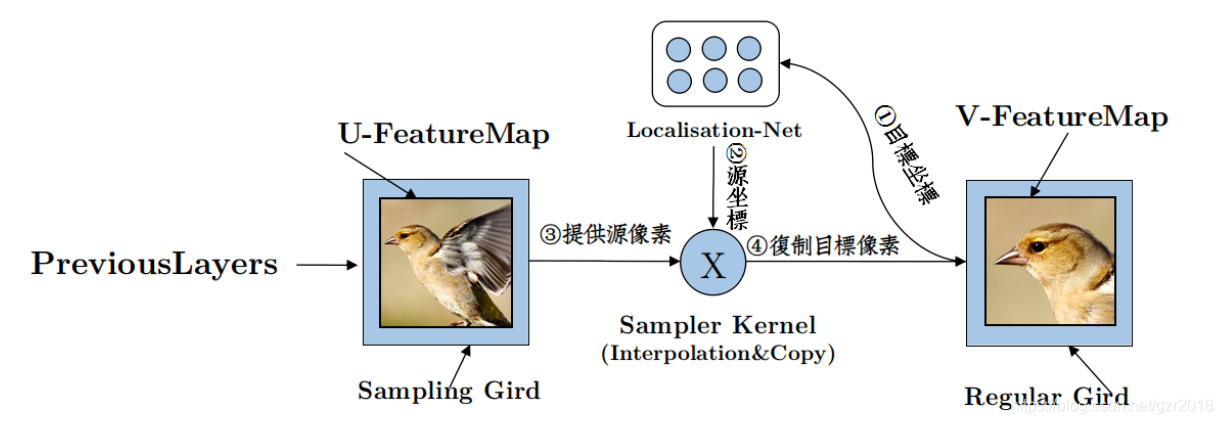
第一部分为为”localization net”,网络中的参数则为空间变换网络需要训练的参数;第二部分就是空间变换即仿射变换,“Grid generator”。
可以结合下图理解,我们的目标是把原始图片(Sampling Grid)中的点转化到规范空间(Regular Grid)中,使用反向传播更新参数,即”localization net”,得到参数,一个矩阵乘法即可变化原始坐标点。
网络结构
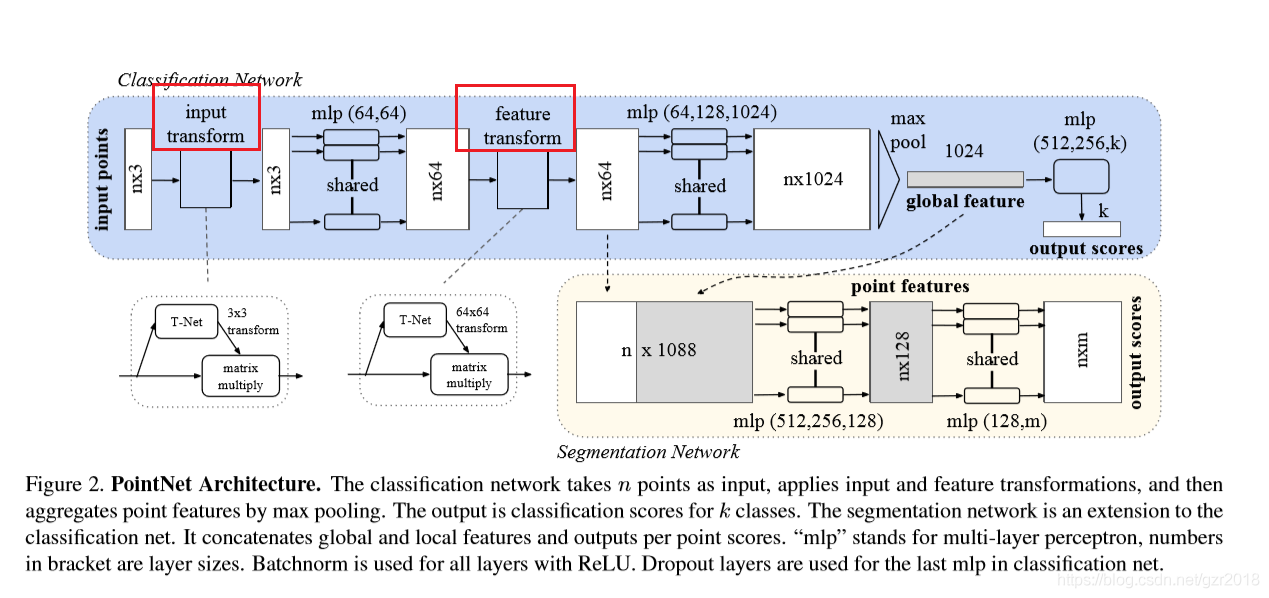
分类网络:
可以看到网络输入是\(n\times3\),首先经过一个input transform网络,网络具体细节如下,其实可以看出一个输入变化网络结构和分类网络的卷积层和全连接层结构高度类似:
T-Net模型,卷积:64--128--1024 全连接:1024--512--256--3*K。代码注释十分清晰了。
def input_transform_net(point_cloud, is_training, bn_decay=None, K=3):
""" Input (XYZ) Transform Net, input is BxNx3 gray image
Return:
Transformation matrix of size 3xK """
# K表示数据的维数,所以这里是3
batch_size = point_cloud.get_shape()[0].value
num_point = point_cloud.get_shape()[1].value
input_image = tf.expand_dims(point_cloud, -1) # 转为4D张量,-1表示在最后加入一维,比如shape[2,3]->shape[2,3,1]
# 构建T-Net模型,64--128--1024
# tf_util.conv2d是对数据做卷积,使用[1,3]的模板卷积,就变成了num_point*1*64。生成64个通道
net = tf_util.conv2d(input_image, 64, [1,3],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='tconv1', bn_decay=bn_decay)
# 每一个卷积核的大小为 [kernel_h, kernel_w,num_in_channels, num_output_channels]
# 使用[1,1]的模板卷积。生成128个通道
net = tf_util.conv2d(net, 128, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='tconv2', bn_decay=bn_decay)
# 使用[1,1]的模板卷积。生成1024个通道
net = tf_util.conv2d(net, 1024, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='tconv3', bn_decay=bn_decay)
# 最大池化,模板大小[num_point,1],也就是一组点的一个通道仅保留一个feature,实现对称。
net = tf_util.max_pool2d(net, [num_point,1],
padding='VALID', scope='tmaxpool')
# 注意上面模板都是对一组batch做的卷积,下面这句话应该就是参数拉直,之前大小应该是[batch_size,1,1024]做下面的fc层
net = tf.reshape(net, [batch_size, -1])
# net的大小应该是[bacth_size,1024],即每组点只保留1024个feature
net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
scope='tfc1', bn_decay=bn_decay)
net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
scope='tfc2', bn_decay=bn_decay)
# 两个fc,最后输出256维特征
# 生成点云旋转矩阵 T=3*3
with tf.variable_scope('transform_XYZ') as sc:
assert(K==3)
# 创建变量
weights = tf.get_variable('weights', [256, 3*K],
initializer=tf.constant_initializer(0.0),
dtype=tf.float32)
biases = tf.get_variable('biases', [3*K],
initializer=tf.constant_initializer(0.0),
dtype=tf.float32)
biases += tf.constant([1,0,0,0,1,0,0,0,1], dtype=tf.float32)
# [batch_size,256]*[256,3*k]->[bacth_size,3*k]变化矩阵
transform = tf.matmul(net, weights)
# 加上bias
transform = tf.nn.bias_add(transform, biases)
transform = tf.reshape(transform, [batch_size, 3, K])
return transform
feature transform 网络结构和input transform基本一样,就是变化矩阵式KK,PointNet网络结构就是6464,因为待变化矩阵大小是\(n*64\)。
def feature_transform_net(inputs, is_training, bn_decay=None, K=64):
""" Feature Transform Net, input is BxNx1xK
Return:
Transformation matrix of size KxK """
batch_size = inputs.get_shape()[0].value
num_point = inputs.get_shape()[1].value
net = tf_util.conv2d(inputs, 64, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='tconv1', bn_decay=bn_decay)
net = tf_util.conv2d(net, 128, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='tconv2', bn_decay=bn_decay)
net = tf_util.conv2d(net, 1024, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='tconv3', bn_decay=bn_decay)
net = tf_util.max_pool2d(net, [num_point,1],
padding='VALID', scope='tmaxpool')
net = tf.reshape(net, [batch_size, -1])
net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
scope='tfc1', bn_decay=bn_decay)
net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
scope='tfc2', bn_decay=bn_decay)
with tf.variable_scope('transform_feat') as sc:
weights = tf.get_variable('weights', [256, K*K],
initializer=tf.constant_initializer(0.0),
dtype=tf.float32)
biases = tf.get_variable('biases', [K*K],
initializer=tf.constant_initializer(0.0),
dtype=tf.float32)
biases += tf.constant(np.eye(K).flatten(), dtype=tf.float32)
transform = tf.matmul(net, weights)
transform = tf.nn.bias_add(transform, biases)
transform = tf.reshape(transform, [batch_size, K, K])
return transform
分析完两个transform网络之后,就十分清晰了,我们看一下分类网络的代码:
def get_model(point_cloud, is_training, bn_decay=None):
""" Classification PointNet, input is BxNx3, output Bx40 """
batch_size = point_cloud.get_shape()[0].value
num_point = point_cloud.get_shape()[1].value
end_points = {}
with tf.variable_scope('transform_net1') as sc:
# 得到输入变换网络
transform = input_transform_net(point_cloud, is_training, bn_decay, K=3)
# 矩阵乘法,变换到规范空间
point_cloud_transformed = tf.matmul(point_cloud, transform)
# 转为4D张量
input_image = tf.expand_dims(point_cloud_transformed, -1)
# 卷积核[1,3],输出通道64
net = tf_util.conv2d(input_image, 64, [1,3],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv1', bn_decay=bn_decay)
# 卷积核[1,1],输出通道64
net = tf_util.conv2d(net, 64, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv2', bn_decay=bn_decay)
# 第二个:特征变化网络
with tf.variable_scope('transform_net2') as sc:
transform = feature_transform_net(net, is_training, bn_decay, K=64)
end_points['transform'] = transform
net_transformed = tf.matmul(tf.squeeze(net, axis=[2]), transform)
net_transformed = tf.expand_dims(net_transformed, [2])
# 卷积层,[1,1]卷积核,输出通道64
net = tf_util.conv2d(net_transformed, 64, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv3', bn_decay=bn_decay)
# 卷积层,[1,1]卷积核,输出通道128
net = tf_util.conv2d(net, 128, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv4', bn_decay=bn_decay)
# 卷积层,[1,1]卷积核,输出通道1024
net = tf_util.conv2d(net, 1024, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv5', bn_decay=bn_decay)
# Symmetric function: max pooling
net = tf_util.max_pool2d(net, [num_point,1],
padding='VALID', scope='maxpool')
net = tf.reshape(net, [batch_size, -1])
# fc
net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
scope='fc1', bn_decay=bn_decay)
# dropout,防止过拟合
net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
scope='dp1')
net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
scope='fc2', bn_decay=bn_decay)
net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
scope='dp2')
# 40,应该是实现40分类
net = tf_util.fully_connected(net, 40, activation_fn=None, scope='fc3')
# return 的是分类网络的结果和n*64的原始特征,可以用分割网络
return net, end_points
文章提到的参数共享的mlp就是卷积运算。以上就是分类网络模型的建立,网络结构还是十分简洁的。
分割网络结构:
整合局部和全局信息,对于点云分割任务,我们需要将局部和全局信息结合起来。
这里,PointNet将经过特征变换后的信息称作局部信息,它们是与每一个点紧密相关的;我们将局部信息和全局信息简单地连接起来,就得到用于分割的全部信息。
def get_model(point_cloud, is_training, bn_decay=None):
""" Classification PointNet, input is BxNx3, output BxNx50 """
batch_size = point_cloud.get_shape()[0].value
num_point = point_cloud.get_shape()[1].value
end_points = {}
with tf.variable_scope('transform_net1') as sc:
transform = input_transform_net(point_cloud, is_training, bn_decay, K=3)
point_cloud_transformed = tf.matmul(point_cloud, transform)
input_image = tf.expand_dims(point_cloud_transformed, -1)
net = tf_util.conv2d(input_image, 64, [1,3],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv1', bn_decay=bn_decay)
net = tf_util.conv2d(net, 64, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv2', bn_decay=bn_decay)
with tf.variable_scope('transform_net2') as sc:
transform = feature_transform_net(net, is_training, bn_decay, K=64)
end_points['transform'] = transform
net_transformed = tf.matmul(tf.squeeze(net, axis=[2]), transform)
point_feat = tf.expand_dims(net_transformed, [2])
print(point_feat)
net = tf_util.conv2d(point_feat, 64, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv3', bn_decay=bn_decay)
net = tf_util.conv2d(net, 128, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv4', bn_decay=bn_decay)
net = tf_util.conv2d(net, 1024, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv5', bn_decay=bn_decay)
global_feat = tf_util.max_pool2d(net, [num_point,1],
padding='VALID', scope='maxpool')
# 得到1024的全局特征
print(global_feat)
# expand到点的特征上,构成拓展的全局特征
global_feat_expand = tf.tile(global_feat, [1, num_point, 1, 1])
concat_feat = tf.concat(3, [point_feat, global_feat_expand])
print(concat_feat)
# 卷积层
net = tf_util.conv2d(concat_feat, 512, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv6', bn_decay=bn_decay)
net = tf_util.conv2d(net, 256, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv7', bn_decay=bn_decay)
net = tf_util.conv2d(net, 128, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv8', bn_decay=bn_decay)
net = tf_util.conv2d(net, 128, [1,1],
padding='VALID', stride=[1,1],
bn=True, is_training=is_training,
scope='conv9', bn_decay=bn_decay)
# 50分类,就是网络图中的m
net = tf_util.conv2d(net, 50, [1,1],
padding='VALID', stride=[1,1], activation_fn=None,
scope='conv10')
net = tf.squeeze(net, [2]) # BxNxC
return net, end_points
以上就是PointNet网络结构,如果只想了解PointNet网络结构,看到这里已经差不多了。我们已经了解了为什么需要变化网络,为什么需要对称函数。
我们再看论文中的如下表示,就能理解了,\(x\)理解为每一个点,\(h(x)\)理解为提取这点的k维特征,\(g(h(x_1),....,h(x_n))\)理解成一个从\(n*k\)空间中映射到实数域的对称函数。
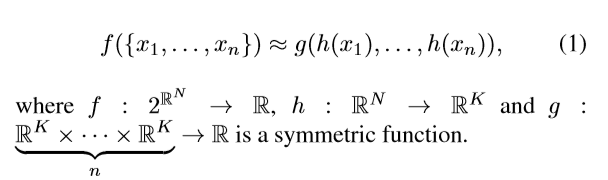
鲁班性分析
说明对于任何输入数据集,都存在一个关键集和一个最大集,使得对和之间的任何集合,其网络输出都和一样。这也就是说,模型对输入数据在有噪声和有数据损坏的情况都是鲁棒的。
关键集和最大集的样例:

参考:
PointNet:基于深度学习的3D点云分类和分割模型
空间变换网络--spatial transform network



 浙公网安备 33010602011771号
浙公网安备 33010602011771号