递归算法典型特征及经典递归例子代码实现

递归（recursion）：程序调用自身的编程技巧。

  递归满足2个条件：

    1）有反复执行的过程（调用自身）

    2）有跳出反复执行过程的条件（递归出口）

递归算法的通用解法：

1.  
   f(para......){
2.  
   if(...)//终止条件
3.  
   {...//递归的终止项，一般是最低项
4.  
   }
5.  
   else{//继续递归
6.  
   ...//譬如for循环，遍历所有可能路径
7.  
   ...//某些递归逻辑，注意回退事件
8.  
   }

递归算法的典型例子：

（1）阶乘

 n! = n * (n-1) * (n-2) * ...* 1(n>0)

1.  
   <pre name="code" class="html">//阶乘
2.  
   int recursive(int i)
3.  
   {
4.  
   int sum = 0;
5.  
   if (0 == i)
6.  
   return (1);
7.  
   else
8.  
   sum = i * recursive(i-1);
9.  
   return sum;
10.  
    }

 

（2）汉诺塔

1.  
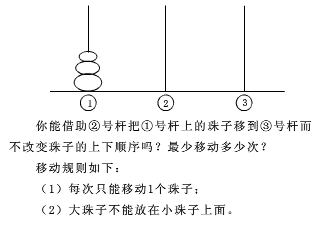
   void hanoi(int n,int p1,int p2,int p3)
2.  
   {
3.  
   if(1==n)
4.  
   cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
5.  
   else
6.  
   {
7.  
   hanoi(n-1,p1,p3,p2);
8.  
   cout<<"盘子从"<<p1<<"移到"<<p3<<endl;
9.  
   hanoi(n-1,p2,p1,p3);
10.  
    }
11.  
    }

（3）全排列

第二位之后的数，依次和第一位交换···   依次做第一，剩下的全排序

 如1,2,3三个元素的全排列为：

  1,2,3

  1,3,2

  2,1,3

  2,3,1

  3,1,2

  3,2,1 

1.  
   void Perm(int list[],int k,int m)
2.  
   {
3.  
   if (k == m-1)
4.  
   {
5.  
   for(int i=0;i<m;i++)
6.  
   {
7.  
   printf("%d",list[i]);
8.  
   }
9.  
   printf("n");
10.  
    }
11.  
    else
12.  
    {
13.  
    for(int i=k;i<m;i++)
14.  
    {
15.  
    Swap(list[k],list[i]);
16.  
    Perm(list,k+1,m);
17.  
    Swap(list[k],list[i]);
18.  
    }
19.  
    }
20.  
    }

（4）斐波那契数列

  斐波纳契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……

  这个数列从第三项开始，每一项都等于前两项之和。

1.  
   long Fib(int n)
2.  
   {
3.  
   if (n == 0)
4.  
   return 0;
5.  
   if (n == 1)
6.  
   return 1;
7.  
   if (n > 1)
8.  
   return Fib(n-1) + Fib(n-2);
9.  
   }

（5）八皇后

1.  
   void Backtrack(int k,int cnt)
2.  
   {//回溯算法主程序
3.  
    
4.  
   if(k < 0 || cnt == n)//棋牌摆放完毕 or 以摆满n后
5.  
   {
6.  
   if(cnt == n)
7.  
   {
8.  
   printf("No.%d:\n",++total);
9.  
   for(int i = 0; i < n; i++)
10.  
    {
11.  
    for(int j = 0; j < n; j++)
12.  
    printf(" %c ",Chess[i][j]);
13.  
    putchar('\n');
14.  
    }
15.  
    putchar('\n');
16.  
    }
17.  
    }
18.  
    else
19.  
    {
20.  
    int r = k / n, c = k % n;
21.  
    if(Judge(r,c))
22.  
    {//可放置一皇后
23.  
    Chess[r][c] = queen;
24.  
    Backtrack(k-1,cnt+1);
25.  
    Chess[r][c] = blank;//不行的话就要回退重置
26.  
    }
27.  
    Backtrack(k-1,cnt);
28.  
    }
29.  
     
30.  
    }

（6）选择题

 1、排列组合解法：
从A到Z可以理解为：
横向的距离为4个单元
纵向的单元为2个单元
这个理解的基础上，这个问题就转化为排列组合问题了。
求最短路径条数，其实就是把这个横向的4个单元和纵向的2个单元进行组合就行了。
所以，从A到Z的最短路径条数为C(6,2)=15
但是题目给出的是右上角和左下角各自缺了一块，所以要减掉2种情况。
所以，最后的最后，结果是C（6,2）-2=13.

2、递归式解法

（7）最大公约数之辗转相除法

 

7.1 递归实现

 

int gcd(int a, int b)
{
        if(!b) return a;
        else  return gcd(b, a%b );
}

 

7.2 迭代实现

 

int gcd(int a, int b)
{
        int c = a%b;
        while(c){
                a = b;
                b = c;
                c = a % b;
        }
        return b;
}