子集 - 迭代法和递归法

1.题目描述

给你一个整数数组nums，返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。
示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

2.题解

2.1 迭代法

class Solution {
    List<Integer> t = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        for (int mask = 0; mask < (1 << n); ++mask) {
            t.clear();
            for (int i = 0; i < n; ++i) {
                if ((mask & (1 << i)) != 0) {
                    t.add(nums[i]);
                }
            }
            ans.add(new ArrayList<Integer>(t));
        }
        return ans;
    }
}

注意到这里1 << n和1 << i都用了位运算的左移操作。

以nums = [1,2,3]为例：
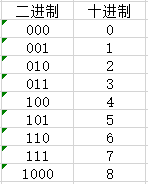
mask < (1 << n)，即mask < 8。
mask & (1 << i)，即mask & 001、mask & 010、mask & 100。
当mask = 0时，mask & (1 << i)为0，所以这里会向集合ans添加一个空的集合t。
当mask = 1时，001 & 001 != 0，所以这里会向集合t添加一个nums[0]。注意，1左移0位为001。
当mask = 3时，011 & 001 != 0，011 & 010 != 0，所以这里会向集合t添加nums[1]和nums[2]。

2.2 递归法

class Solution {
    List<Integer> t = new ArrayList<Integer>();
    List<List<Integer>> ans = new ArrayList<List<Integer>>();

    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }

    public void dfs(int cur, int[] nums) {
        if (cur == nums.length) {
            ans.add(new ArrayList<Integer>(t));
            return;
        }
        t.add(nums[cur]);
        dfs(cur + 1, nums);
        t.remove(t.size() - 1);
        dfs(cur + 1, nums);
    }
}

以nums = [1,2,3]为例：

dfs cur=0 t=1
      dfs cur=1 t=1,2
            dfs cur=2 t=1,2,3
                  dfs cur=3 添加[1,2,3]
            dfs cur=2 t=1,2
                  dfs cur=3 添加[1,2]
      dfs cur=1 t=1
            dfs cur=2 t=1,3
                  dfs cur=3 添加[1,3]
            dfs cur=2 t=1
                  dfs cur=3 添加[1]
dfs cur=0 
      dfs cur=1 t=2
            dfs cur=2 t=2,3
                  dfs cur=3 添加[2,3]
            dfs cur=2 t=2
                  dfs cur=3 添加[2]
      dfs cur=1
            dfs cur=2 t=3
                  dfs cur=3 添加[3]
            dfs cur=2
                  dfs cur=3 添加[]

注意，递归的边界条件为cur == nums.length，cur是调用方法dfs时传入的，而不是集合t的元素个数。
参考：

• 子集 - 子集 - 力扣（LeetCode）