3月20日晚训 & CF题目讲解
Detective Task
题面翻译
房屋里有一幅画， \(n\) 个人依次进入房间。前一个人出之后后一个人再进。 \(n\) 个人都出房间后画不见了。每个人只知道自己是不是小偷和他在房间里时画还在不在。
现在审问这 \(n\) 个人，每个人可以回答 1 表示他在房子里时画在， 0 表示不在， ? 表示忘了。小偷会随便回答一个答案，其他人是诚实的。
现在你需要求出，有几个人可能是小偷。
询问数 \(\leq 10^4\) ， \(\sum n\leq 2\times 10^5\) 。保证输入合法。
思路解析
本题的相关知识点是贪心+逻辑。
提示一：画只有一幅，所以小偷只有一个人，其他人都说真话。
提示二：有画的时候，老实人只会说?或者1，没有画的时候，老实人只会说?或者0
提示三：判断一个人可能是小偷，那么他前面的答案只会存在1或者?，同理他后面答案只会存在0或者?
本题完整思路如下：首先，枚举每一个人是否可能为小偷，对于这个人，判断其是否为小偷的标准为，他前面的答案没有0，后面的答案不存在1。然后统计符合条件的人数即可。
注释代码
#include <bits/stdc++.h>
using namespace std;
int t,n;
string a;
inline void init()//核心代码块
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>t;
while(t--)
{
cin>>a;
a=" "+a;
n=a.size()-1;
int cnt=0,ans=0;
//小偷个数只有1个，因为只有一幅画，但是可能人选会有好几个
for(int i=1; i<=n; i++)
if(a[i]=='1')//统计全场有多少个1
cnt++;
//小偷之前的人，都说1和？，后面的人都说0和？，因为他们都是诚实人
for(int i=1; i<=n; i++)
{
//判断i是不是小偷
if (a[i-1]=='0')//前面出现0了，那么后面的人都不可能被判定为小偷了，因为小偷的答案前面都是1或者？
break;
if (a[i]=='1')//当前是1，后面的1个数再次减少
cnt--;
if (cnt==0)//后面没有1了，那么都是0或者？了，不存在1了
ans++;
}
cout<<ans<<endl;//输出符合条件的个数
}
}
signed main()
{
init();
return 0;
}
A-B-C Sort
题面翻译
你有三个数组 \(a,b,c\)，\(a\) 初始有 \(n\) 个元素，\(b\) 和 \(c\) 初始是空的。
你可以执行以下算法：
第一步，当 \(a\) 不为空，重复从 \(a\) 取出末尾的元素并将其插入 \(b\) 的正中间。如果 \(b\) 当前有奇数个元素，可以选择将 \(a\) 中取出的元素插入 \(b\) 正中间元素紧挨着的左侧或右侧的空位上。
在此之后 \(a\) 变成空的，\(b\) 有 \(n\) 个元素。
第二步，当 \(b\) 不为空，重复取出 \(b\) 正中间的元素并将其插入 \(c\) 的末尾。如果 \(b\) 当前有偶数个元素，可以选择从正中间两个元素中取出一个。
在此之后 \(b\) 变成空的，\(c\) 有 \(n\) 个元素。
具体流程可以参照样例解释。求你是否可以通过以上算法让 \(c\) 以非降序排序。 如果能，输出一行 YES，否则输出 NO。
思路解析
应该是今天晚上最难的一道训练题目，我的解释能力可能有限，不懂的可以问问@mushanyu,@kyline
提示一：a和c数组已知，只有b数组未知
我们先讨论YES的情况，在这里，我们将a序列非降序排序，即可得到C序列，那么此时a,c序列我们都将是已知的情况。
观察题目的操作，我们会发现由a数组变成b数组，和由b数组变成c数组恰好是互逆操作
换句话说，我们a数组和c数组，变成b数组，属于同一种操作，都是从末尾删除数字，然后放到b数组正中间。
那么如果说a和c数组可以生成一份相同的b数组，那么显然，我们就可以实现从a数组变成b数组，然后变成c数组。
提示二：b数组每一次更新后的左右端点和a,c数组的末尾节点存在关联。
根据题目所给的第一组样例，如图解释：
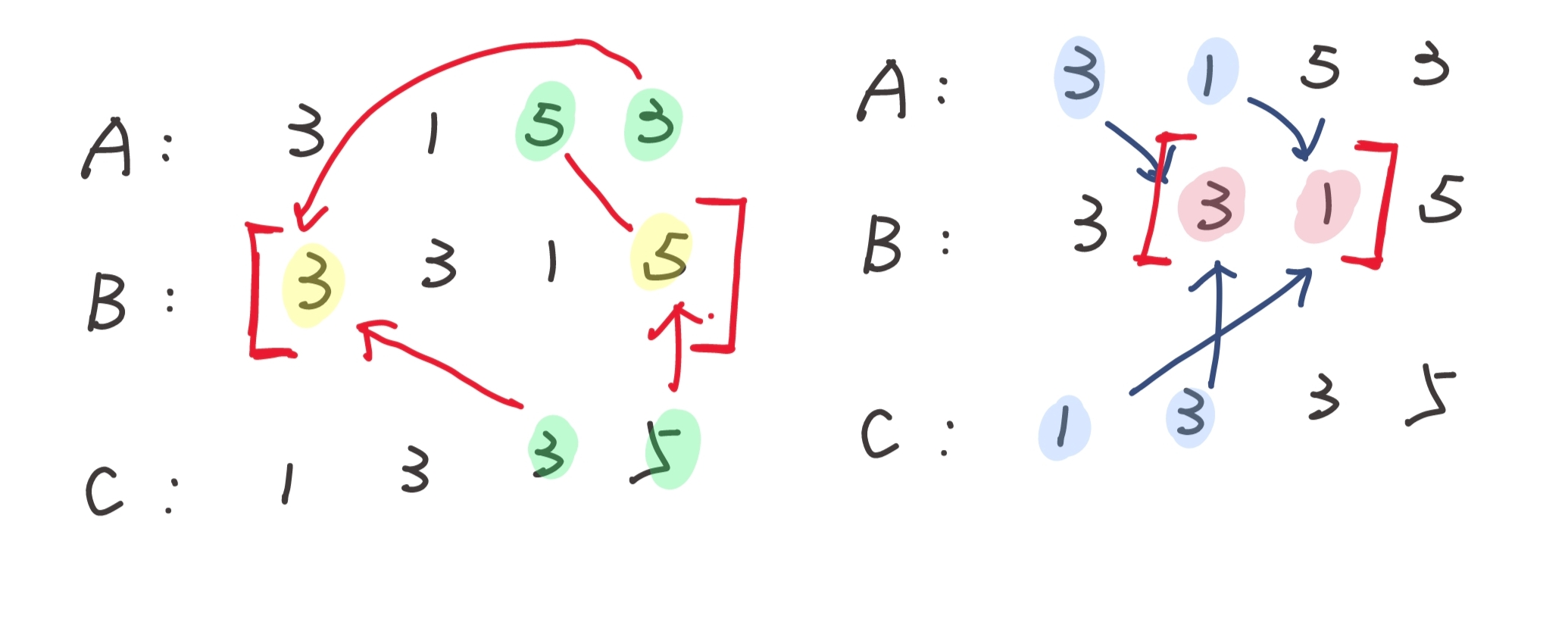
由于b数组并没有确认，是由a和c数组生成，故依次比较 a,c 末尾两个元素，判断能否匹配即可。
注释代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+20;
int t,n,a[N],c[N];
inline void init()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>t;
while(t--)
{
cin>>n;
for(int i=1; i<=n; i++)//获得题目要求的A序列
cin>>a[i],c[i]=a[i];
sort(c+1,c+1+n);//获得题目要求的C序列
//A->B和B->C为相反操作，所以A->C 等价 A,C两序列求相同的B
//b每一对首尾，都来自ac的后两位
int flag=true;
for(int r=n; r>1; r-=2)
{
int l=r-1;
if ( (a[l]==c[l] && a[r]==c[r]) || (a[l]==c[r] && a[r]==c[l]) )
//所以要求ac的末尾两位需要匹配
continue;
cout<<"NO"<<endl;//不匹配
flag=false;
break;
}
if (flag)
cout<<"YES"<<endl;
}
}
signed main()
{
init();
return 0;
}
Infinite Replacement
题面翻译
给一个只含小写字母 a 的字符串 \(s\) 和一个用来替换的字符串 \(t\) 。
你可以将 \(s\) 中任意一个字母 a 用 \(t\) 来替换，替换的次数不限。
对于每一个 \(s\) 和 \(t\) ，你可以得到几个不同的字符串？如果有无限个，输出 -1 。
思路解析
本题考查的知识点是：分类讨论+模拟
首先，原字符串的长度为len，我们先行定义一下
我们首先针对，替换字符串的长度，进行分类讨论。
如果说字符串的长度是1：
此时我们进行一次操作，将单字母a进行替换操作后，我们会发现字符串的长度不会变化
那么如果说替换字符串就是字母a，那么替换毫无意义，我们输出1即可结束。
如果说替换字符串不是字母a，那么对于每一位来说，替换or不替换，都会导致两个不同的字符串生成，于是我们的不同字符串个数将是\(2^n\)个
如果说字符串的长度大于1：
如果说替换字符串内部，存在一个字母a的话，那么就会出现我们可以无限套娃类型的去替换字符串，让字符串长度无限增大
比如说a是原来的字符串，我们替换字符串是abc，那么替换一次后，变成abc，替换两次后变成abcbc，再次替换abcbcbc可以无限增长下去。
那如果说不存在字母a的话，那么对于每一个字母a，他只能替换一次或者不替换，类似于之前所说的方法，答案是\(2^n\)
注释代码
#include <bits/stdc++.h>
using namespace std;
#define int long long//字符串的长度<=50,答案最大2^50
int t,n;
string s,s2;
inline void init()
{
//freopen("stdin.in","r",stdin);
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>t;
while(t--)
{
cin>>s>>s2;
int flag=false;
if (s2.size()==1)//长度为1的字符串，无论怎么替换，串的长度都不会改变
{
int ans=pow(2ll,s.size());
if (s2[0]=='a')//替换没有意义
cout<<1<<endl;
else cout<<ans<<endl;//每一位都可能被替换
continue;
}
for(int i=0; i<s2.size(); i++)
if (s2[i]=='a')//s的一个a字母被串替换后，因为替换的串长度大于2，且含有'a'，还可以替换，所以无穷无尽
flag=true;
if (flag)//串的长度可以无限延生，自然是-1
{
cout<<-1<<endl;
continue;
}
int ans=pow(2ll,s.size());
cout<<ans<<endl;//对于每一位字符，都有替换or不替换的选择
}
}
signed main()
{
init();
return 0;
}
Tree Infection
题面翻译
题意描述
一个树是一个无环连通图。一个有根树有一个被称作“根结点”的结点。对于任意一个非根结点 \(v\) ，其父结点是从根结点到结点 \(v\) 最短路径上的前一个结点。结点 \(v\) 的子结点包括所有以 \(v\) 父结点为 \(v\) 的结点。
给定一个有 \(n\) 个结点的有根树。结点 \(1\) 即为根结点。一开始，该树上所有结点均是“健康”的。
每一秒你会进行两次操作——先是传播操作，然后是注射操作，定义如下。
- 传播操作：对于每个结点 \(v\) ，若该结点至少有一个子结点被“感染”，则你可以“感染”顶点 \(v\) 任意一个其他的子结点。
- 注射：你可以选择任意一个“健康”的结点并使它变为“感染”状态。
这程每秒会重复一次知道整个树的结点都处于“感染”状态。你需要找到使整个树被“感染”的最短时间（秒数）。
输入格式
有多个测试数据。第一行输入整数 \(t\) ，代表有 \(t\) 组数据。每组数据格式如下。
第一行给定整数 \(n\) ，表示整个树共有 \(n\) 个结点。
第二行输入 \(n-1\) 个整数 \(p_{2...i-1}\) ，第 \(p_i\) 个整数表示 \(i\) 号结点的父节点是 \(p_i\) 号结点。
输出格式
共 \(t\) 行，每行一个整数，即使整个树被“感染”的最短时间（秒数）。
数据范围
- $ 1 \le t \le 10^4 $
- $ 2 \le n \le 2 \times 10^5 $
- $ 1 \le p_i \le n $
- $ \sum \limits_{i=1} ^t n_i \le 2 \times 10^5 $
思路解析
相较于上面的分析，思路简短很多，少了一些细节概述，因为相信聪明的你肯定能理解，其实是我晚上敲字敲累了
感染方式要注意，如果一个父节点的儿子节点被感染了，那么这个被感染点的其中一个兄弟节点会被感染。
提示一：一个节点被感染后，只能感染兄弟节点，其儿子节点，父亲节点均不能被感染
提示二：优先感染兄弟节点多的一层节点，对于该层，先接种一次，感染一个节点，随着时间推移，每秒感染一个节点。
提示三：存在一层的节点数量过于多，以至于该层需要接种多次病毒，加快感染速度。
完整思路是：首先获取每一个父亲节点的儿子个数，然后从大到小排序，优先感染节点多的一层，然后二分判断还需要格外接种多少个节点，也就是需要每个层被接种一次后，还要格外接种多少天。
代码解析
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+20;
int t,n,a[N],Size[N];
vector<int> q;
int check(int x)
{
int cnt=0,time=q.size()+x;
for(int i=0; i<q.size(); i++)
//对于当前节点，由于太大，只有一个节点被感染的话，在规定时间内无法被全部感染
cnt+=max(0,q[i]-(time-i));
return cnt<=x;
}
int cmp(int a,int b)
{
return a>b;
}
inline void init()
{
// freopen("stdin.in","r",stdin);
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>t;
while(t--)
{
cin>>n;
for(int i=1; i<=n; i++)
Size[i]=0;
q.clear();
for(int i=1; i<n; i++)
{
int x;
cin>>x;
Size[x]++;//x多一个儿子
}
q.push_back(1);//根节点自己
for(int i=1; i<=n; i++)
if (Size[i])
q.push_back(Size[i]);
sort(q.begin(),q.end(),cmp);//优先感染儿子多的节点 的一个儿子
int l=0,r=n+1,ans=q.size();
//二分需要格外感染的时间,每一个父节点下面都需要至少有一个子节点被感染一次，所以至少需要ans=q.size()天
while(l<r)
{
int mid=l+r>>1;
if (check(mid))
r=mid;
else l=mid+1;
}
ans+=l;
cout<<ans<<endl;
}
}
signed main()
{
init();
return 0;
}
