Educational Codeforces Round 67 (Rated for Div. 2) E. Tree Painting

题目链接

Tree Painting

题面翻译

给定一棵 \(n\) 个点的树 初始全是白点

要求你做 \(n\) 步操作，每一次选定一个与一个黑点相隔一条边的白点，将它染成黑点，然后获得该白点被染色前所在的白色联通块大小的权值。

第一次操作可以任意选点。

求可获得的最大权值

思路

假如说，第一次我们已经选择了一个点了，那么接下来的点，我们只需要按照层次遍历，依次选择点即可了。

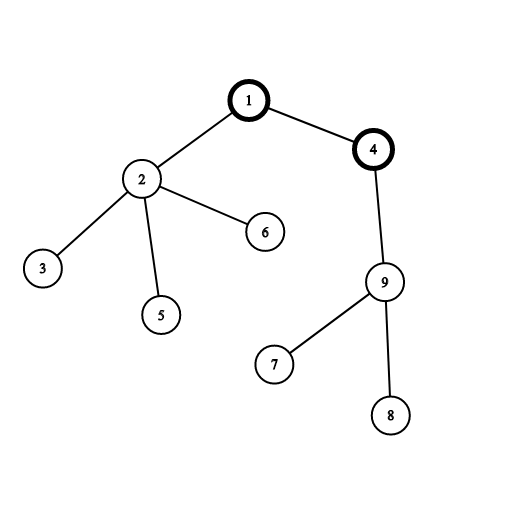
比如说，这里选择1号点后，接下来2，4，3，5，6，9，7，8依次遍历即可，达到选择1号点的最大收益。

我们定义\(f[i]\)为选择\(i\)号点之后可以获得的最大收益，则

\[f_x=size_x+\sum_{i \in son_x}f[i] \]

刚开始选择\(x\)点，首先会获得以\(x\)为根的子树大小的收益（连通块大小），然后接下来选择他的儿子们，会获得他们儿子贡献的收益。

以上的树型DP建立在，我们第一次已经选择好根节点的前提，但是根节点是不确定的，如果每一次都要枚举的话，时间复杂度\(O(n^2)\)是我们无法接受的。

于是我们需要换根DP。

换根DP的核心在于：父子节点关系交换，状态转移方程的修改。

我们还是以下图为例，1号是4号的父亲节点，现在父子关系交换。

此时我们把4号作为根节点，而不是之前的以1号节点作为根节点。

设\(g_x\)表示，以x为根节点，可以得到的最大收益

代码

#include <bits/stdc++.h>
using namespace std;
const int N=2e5+20;
vector<int> G[N];
#define int long long
int a[N],n,m,size[N],f[N],g[N];
void dfs1(int x,int fa)
{
    size[x] = 1;
    for (auto y: G[x])
    {
        if (y == fa)
            continue;
        dfs1(y, x);
        size[x] += size[y];
        f[x] += f[y];
    }
    f[x] += size[x];
}
void dfs2(int x,int fa)
{
    for (auto y: G[x])
    {
        if (y == fa)
            continue;
        g[y] = n + g[x] - 2 * size[y];
        dfs2(y, x);
    }
}
inline void init()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    cin >> n;
    for (int i = 1; i < n; i++)
    {
        int x, y;
        cin >> x >> y;
        G[x].push_back(y);
        G[y].push_back(x);
    }
    dfs1(1,0);
    g[1]=f[1];
    dfs2(1,0);
    int ans=0;
    for(int i=1; i<=n; i++)
        ans=max(ans,g[i]);
    cout<<ans<<endl;
}
signed main()
{
    init();
    return 0;
}