洛谷P5002 专心OI - 找祖先
题目概括
题目描述
这个游戏会给出你一棵树,这棵树有\(N\)个节点,根结点是\(R\),系统会选中\(M\)个点\(P_1,P_2...P_M\).
要Imakf回答有多少组点对\((u_i,v_i)\)的最近公共祖先是\(P_i\)。
Imakf是个小蒟蒻,他就算学了LCA也做不出,于是只好求助您了。
Imakf毕竟学过一点OI,所以他允许您把答案模 \((10^9+7)\)
输入输出格式
输入格式
第一行 \(N , R , M\) 此后\(N-1\)行 每行两个数\(a,b\) 表示\(a,b\)之间有一条边 此后\(1\)行 \(M\)个数 表示\(P_i\)
输出格式
\(M\)行,每行一个数,第\(i\)行的数表示有多少组点对\((u_i,v_i)\)的最近公共祖先是\(P_i\)
输入输出样例
输入样例 #1
7 1 3
1 2
1 3
2 4
2 5
3 6
3 7
1 2 4
输出样例 #1
31
7
1
样例解释
样例1
对于询问1
\[(1,1) (1,2) (1,3) (1,4) (1,5) (1,6) (1,7) \\\\
(2,1) (2,3) (2,6) (2,7) (3,1) (3,2) (3,4) (3,5) \\\\
(4,1) (4,3),(4,6) (4,7) \\\\
(5,1) (5,3) (5,6) (5,7) \\\\
(6,1) (6,2) (6,4) (6,5) \\\\
(7,1) (7,2) (7,4) (7,5)
\]
共31组
询问2
\[(2,2) (2,4) (2,5)\\\\
(4,2) (4,5) \\\\
(5,2) (5,4)
\]
共7组
对于询问3
\[(4,4)
\]
共1组
\[N \leq 10000,M \leq 50000
\]
解题报告
题意理解
-
就是问你有多少个数对,以\(P_i\)为最近公共祖先.
-
然后有\(m\)次查询
算法解析
这道题目,其实只考到了\(Lca\)概念,然后就没有然后了.
\[满足Lca(a,b)=x条件,合法数对为(a,b)\\
\]
我们分析一下,满足条件的数对,有哪些特性.
-
\((a,b)\)不同属于x一个子节点的子树,反例如下
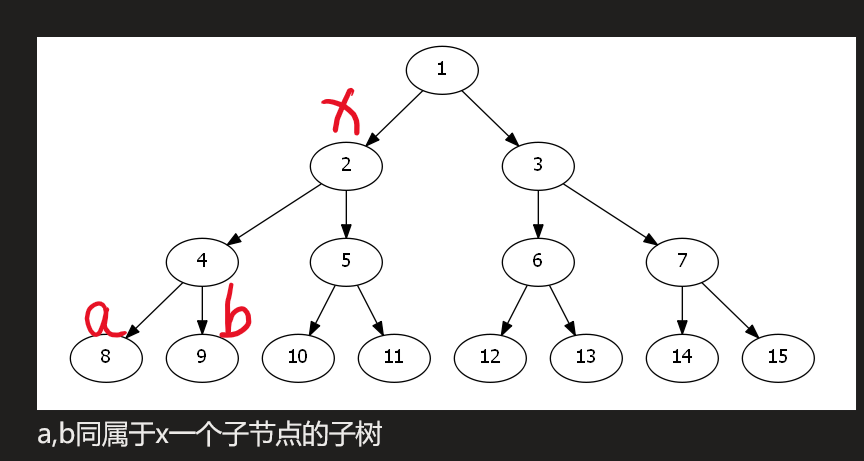
-
\((a,b)\)必须都属于x的子树.反例如下
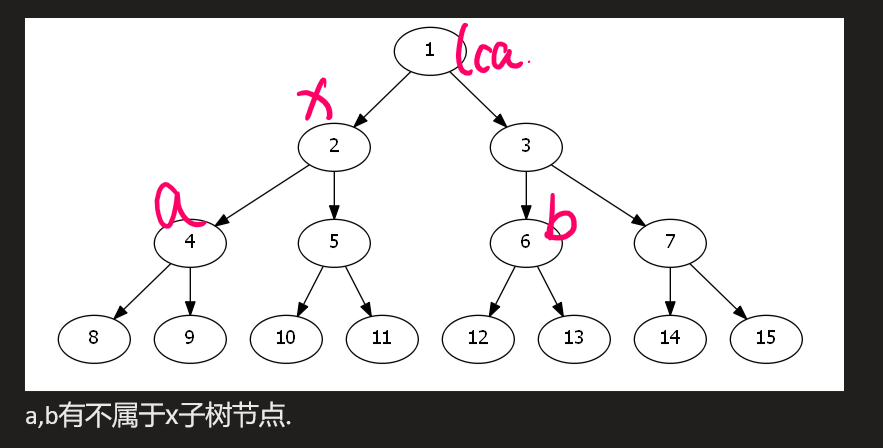
-
\((a,b)\)分别属于,\(x\)不同的儿子的子树节点.正确如下所示

-
\((a,b)\)之中有一个是\(x\),另外一个是\(x\)的子树节点
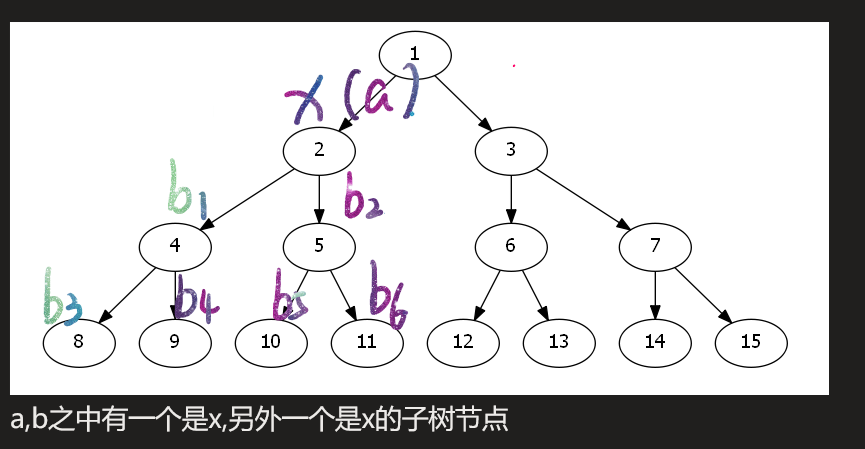
-
\((a,b)\)都是\(x\).
懒得画图了
因此,我们总结得出以上规律.
然后如何统计个数呢.
\[size[x][i]表示x的第i个儿子节点的子树大小,包括儿子节点i \\\\k表示x的儿子节点总数 \\\\Size[x]表示x的子树节点个数,包括x
\]
然后我们开始分类讨论.
- \((a,b)\)都是\(x\)子树节点.
\[size[x][1] \times size[x][2] \times 2 \quad 其中一类\\\\任选两个儿子节点,子树相乘,再加上有序数对,所以乘以2 \\\\\sum_{i=1}^{k}{\sum_{j=1}^{k}size[x][i] \times size[x][j]} \\\\\Rightarrow \sum_{i=1}^{k}{size[x][i] \times (Size[x]-1)} \\\\\Rightarrow (Size[x]-1) \times (Size[x]-1)
\]
然后重复计算了\(a=b\)的情况.
\[\sum_{i=1}^{k}{size[x][i]^2}
\]
于是最后要记得减去.
- \((a,b)\)中有节点是\(x\)
于是我们很容易得出.
\[2 \times Size[x] -1 \quad -1是因为(x,x)算了两次
\]
综上所述,我们得出答案为.
\[ans=(2 \times Size[x]-1)+(Size[x]-1)^2-(\sum_{i=1}^{k}{size[x][i]^2})
\]
代码解析
#include <bits/stdc++.h>
using namespace std;
const int N=10000+20,Mod=1e9+7;
int n,r,m,size[N],root;
long long ans[N],sum[N];
vector<int> g[N];
inline void dfs(int x,int fa)
{
size[x]=1;
for(int y:g[x])
{
if (y==fa)
continue;
dfs(y,x);
size[x]+=size[y];
sum[x]+=size[y]*size[y];
sum[x]%=Mod;
}
ans[x]=(size[x]*size[x]-sum[x])%Mod;
}
inline void init()
{
scanf("%d%d%d",&n,&r,&m);
for(int i=1; i<n; i++)
{
int a,b;
scanf("%d%d",&a,&b);
g[a].push_back(b);
g[b].push_back(a);
}
dfs(r,r);
while(m--)
{
int x;
scanf("%d",&x);
printf("%lld\n",ans[x]);
}
}
signed main()
{
init();
return 0;
}


