[USACO15FEB]Superbull 超级牛
题意概况
题目描述
\(Bessie\)和她的朋友们正在一年一度的\(Superbull\)锦标赛中打球,而\(Farmer John\)负责让比赛尽可能激动人心。
总共有 \(N\) 支队伍 \(1 \le N \le 2000\) 参加了\(Superbull\)锦标赛。每个团队都有一个 \(1 \dots 2^{30}-1\)的团队ID。
\(Superbull\)是一场淘汰赛 - 在每场比赛之后,\(FJ\)选择淘汰其中一支球队,而被淘汰的球队再也无法参加任何比赛了。当只剩下一支球队时,比赛就结束了。
\(FJ\)注意到一个不寻常的事情:在任何游戏中,两个团队的总分是两个团队ID的按位异或(XOR)。
例如,如果第 \(12\) 队和第 \(20\) 队将参加比赛,则该游戏的得分为 \(24\) 分,因为\({01100} \quad xor \quad {10100} = {11000}\)
FJ想要设计一种比赛方案,让所有比赛的得分总和最大。请帮助\(Farmer John\)组织比赛。
输入输出格式
输入格式:第一行包括一个整数 \(N\) ,下面 \(N\) 行每行包括一个队伍的ID。
输出格式:输出一个整数,代表比赛的最大总得分。
样例解释
让 \(3\) 队与 \(9\) 队进行比赛,并让 \(9\) 队晋级。
然后他让 \(6\) 队和 \(9\) 队对决,让\(6\)队获胜。
最后,第 \(6\) 队和第 \(10\) 队比赛,\(10\)队获胜。
总得分为:\(3 \quad xor \quad 9+6 \quad xor \quad 9+6 \quad xor \quad 10=10+15+12=37。\)
样例输入
4
3
6
9
10
样例输出
37
数据范围
\(1 \le N \le 2000\)
解题报告
题意理解
-
给定\(n\)个人,比\(n-1\)场比赛
-
对于一场比赛的精彩度是两个比赛队伍的编号异或
-
要求所有的比赛的精彩度之和最大.
算法解析
首先,这道题目难在建图上面.
我们可以分析一下,这道题目的比赛模式.
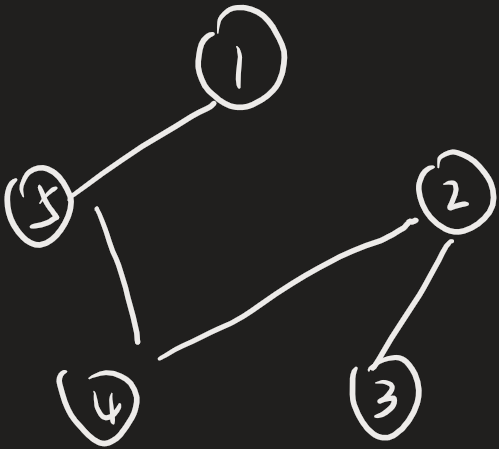
这就是一场竞赛的四场比赛的形式.
我们发现
- 一共比了\(n-1\)场比赛,有\(n\)个人,呈现,树形结构
- 对于一场比赛,谁赢谁输并没有什么影响.
- 我们要求这些边权最大,且只能有\(n-1\)条边
- 一条边的边权,是两点编号的异或.
综上所述,我们可以使用最小生成树的变形,最大生成树来求解本题.
代码解析
#include <bits/stdc++.h>
using namespace std;
const int N=2010;
int a[N],n,m,cnt,fa[N];
struct node
{
int x,y,w;
} g[N*N];
int cmp(node a,node b)//最大排序
{
return a.w>b.w;
}
inline int find(int x)
{
return fa[x]==x?x:fa[x]=find(fa[x]);
}
inline void kruskal()
{
for(int i=1; i<=n; i++)//建立图
for(int j=1; j<=n; j++)
if (i!=j)
g[++cnt]= {i,j,a[i]^a[j]};//边权为异或
sort(g+1,g+1+cnt,cmp);//kruskal排序
int cc=0;
long long ans=0ll;//记得开long long
for(int i=1; i<=cnt; i++)
{
int x=find(g[i].x),y=find(g[i].y);
if (x==y)//已经联合
continue;
fa[x]=y;
ans+=g[i].w;
if (cc==n-1)//n-1条边凑齐了
break;
}
printf("%lld\n",ans);
}
inline void init()
{
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%d",&a[i]),fa[i]=i;
kruskal();
}
signed main()
{
init();
return 0;
}


