树链剖分(轻重链剖分)算法笔记

感谢妄想の岚がそこに大佬指出本文解释不够严谨准确的地方.
感谢妄想の岚がそこに大佬指出本文解释不够严谨准确的地方.
感谢妄想の岚がそこに大佬指出本文解释不够严谨准确的地方.

更好的阅读体验

导言

你会DFS序吗?

我想,你肯定会说会.不会,欢迎点击搜索和DFS序学习

你会线段树吗?不会,欢迎点击暂无

我想,身为巨佬的你肯定会.

既然巨佬你会DFS序,会线段树.那么接下来的树链剖分,你也一定会.

接下来的学习,您必备的算法知识有,DFS序,线段树.

您可以选修的知识点有树上差分,最近公共祖先

---

初学算法

适用范围

1. 将树从x到y结点最短路径上所有节点的值都加上z

我们很容易发现,这个算法就是树上差分算法.

2. 求树从x到y结点最短路径上所有节点的值之和

Lca大佬们,很容易发现这个其实就是Lca算法,然后通过之前我们所介绍的算法性质.

\[dis[x]+dis[y]-dis[Lca(x,y)] \]

就可以计算出,我们需要的答案.

但是假如说,第一问和第二问合二为一,那么我们估计就会有点懵逼了.

巨佬,时间复杂度做不到啊!

因为每一次一条路径上所有节点值都加\(z\),那么每一次都要\(DFS\)一次,重新计算\(dis\)数组.

我们发现了什么?

我们虽然只修改了一条路径上的值,但是我们却为此,去要付出了\(O(n)\)的复杂度,重新扫描一遍树,这也太不划算了.

世界上为什么要有算法?因为有奸商的存在,我们要不停地节省资源.

---

算法来源

一条链,一棵树,他们到底有什么关系呢?

三角关系?情敌关系?婆媳关系?后妈关系?下属关系?

其实啊,我们发现一棵树,是由很多个链构成的.

我们总能,将一棵树,拆分成几条不重叠的链.

一条链,比一棵树好处理多了.

一条链,其实可以看做成一个区间.

区间操作,是我们比较擅长的一类操作,因为他似乎有很多数据结构可以维护.

线段树,树状数组,分块,主席树,平衡树.

似乎样样都可以处理区间操作,而且复杂度都是非常低的.

而且往往,我们都会使用线段树,维护区间.

因为线段树,复杂度低,性质多多,操作多多,代码多多,烦恼多多,反正多多就对了.

假如说,我们可以把一棵树,划分成为一条条链,然后维护这些链,多好啊.

因此我们强势引出了,树链剖分算法.

算法概念

所谓的树链剖分算法,其实和他的名字一样.

就是将一棵树,划分成一些链,然后维护这些链,达到维护整棵树的作用.

某位大佬说过,算法如果可以现实化,与生活贴切,那么将会很容易理解这个算法.

我们现在考虑一个情景.

现在Acwing公司成立了,总裁y总要确立各大部门的负责人.

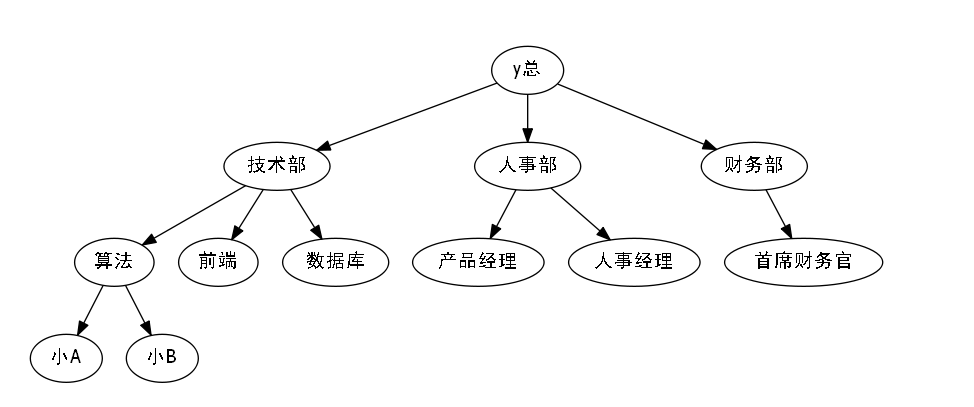
众所周知,不同的职业,薪水是不一样.

因此我们按照,薪水的多少,划分一下每一部门.

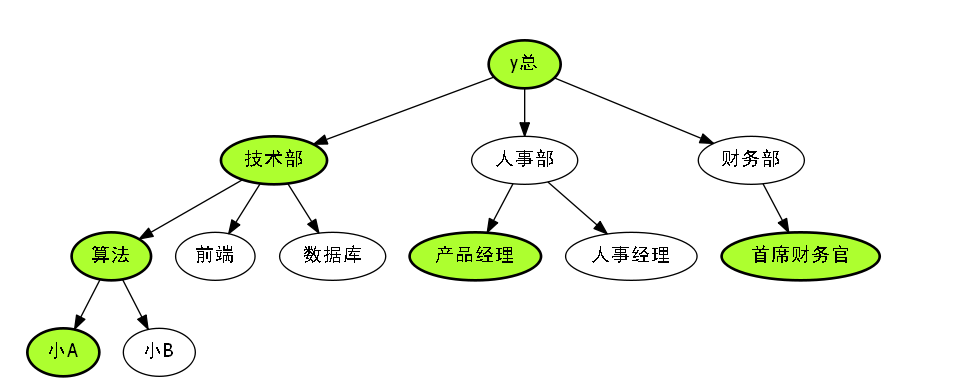
这些高亮的节点,就是我们每一部分,每一阶级的高薪水的大佬们.

我们发现,这些儿子节点多,也就是员工多的节点,才会高亮.

富的流油,一般都会胖的流油,而这些胖的流油,肯定也就重的流油.

所以我们把这些油光发亮的节点称之为,重儿子.

定义	概念
重儿子	父亲节点的所有儿子中子树结点数目最多的结点

那么有富得流油,自然也就有穷的没油.逻辑黑洞,话说没油什么鬼

穷的没油,一般都会瘦的没油,而这些瘦的没油,肯定也就轻的没油.

所以我们把这些黯淡无光的节点称之为,轻儿子.

定义	概念
轻儿子	父亲节点中除了重儿子以外的所有儿子节点

一般来说,有钱的部门,升迁都升迁的快,涨工资也涨得快,不然怎么叫作热门部门.

因此我们再来看一下这些升迁快的路径.

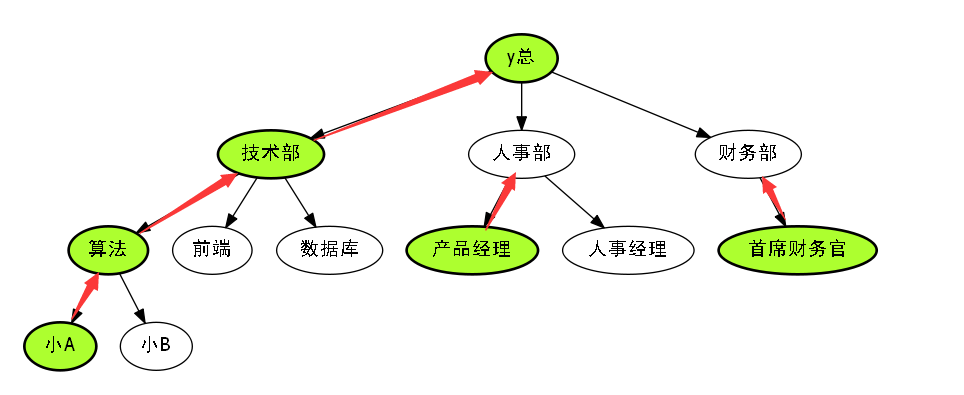
红色代表着升迁快的边,也就是重边.

我们发现,这些升迁快的边,都是重儿子往上走的边.

因此我们得出概念.

定义	概念
重边	父亲结点和重儿子连成的边

有些部门升迁快,当然也有些部门升迁慢,因此我们升迁不快的边,都认为是轻边.

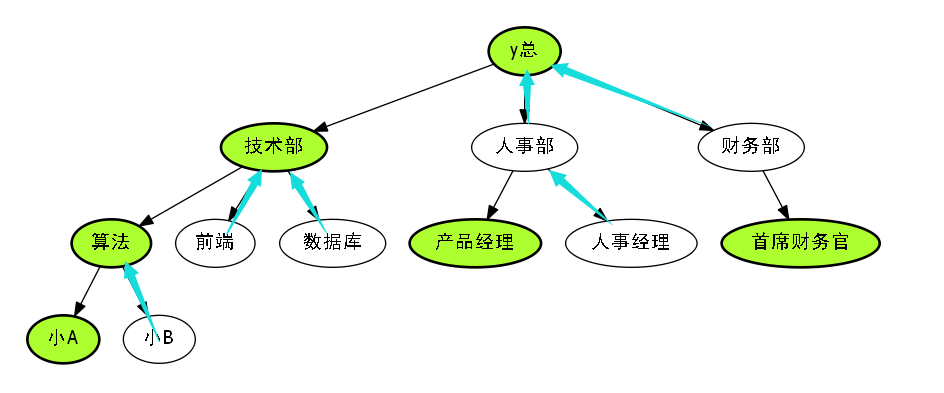
蓝色代表着升迁慢的边,也就是轻边.

我们发现轻边,都是轻儿子往上的边.

所以概念也就显而易见了.

定义	概念
轻边	父亲节点和轻儿子连成的边

一时之间升迁快,不代表着有前途,一直都升迁快,才叫做前途光明

因此你想要在Acwing公司里面,找到一些前途路径.

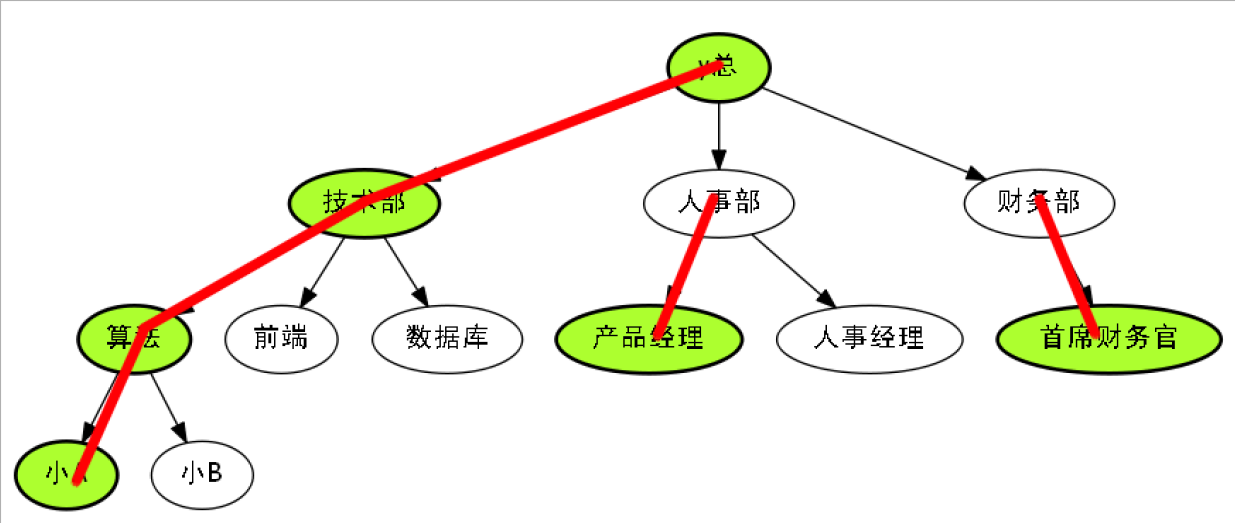
一条红边,也可以看作前途路径.

一条前途路径,由多个升迁快的边构成,当然只有一个也木有问题.

定义	概念
重链	由多条重边连接而成的路径；

不红的路径也不少,几家欢喜几家愁,一个公司不可能天天升迁.

因此我们也会找到冷门路径.

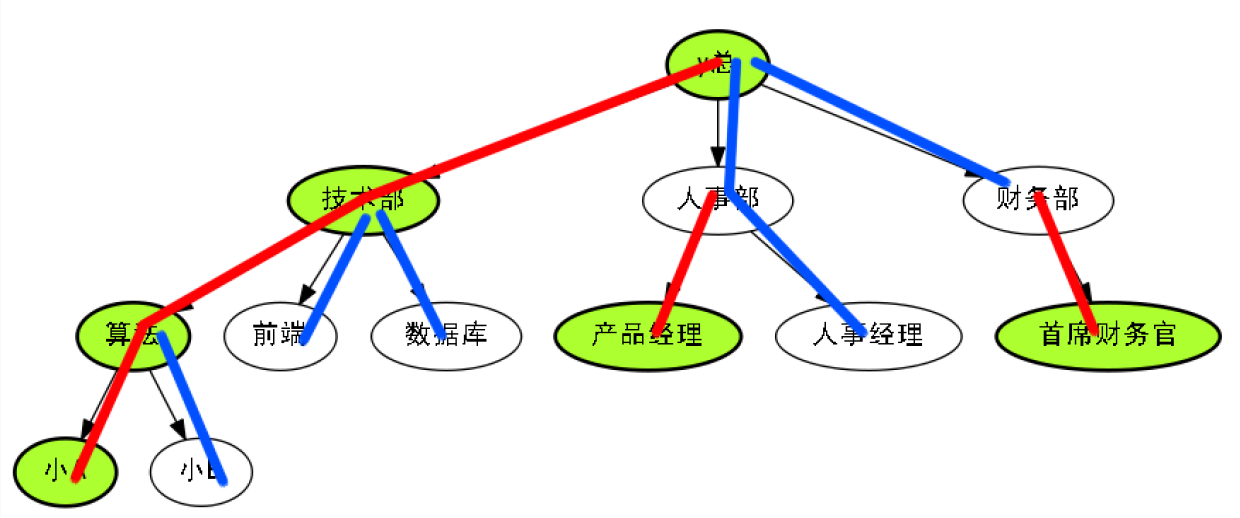
定义快乐似神仙.

定义	概念
轻链	由多条轻边连接而成的路径

经过上面这个故事解说下,现在秦淮岸相信各位巨佬,对于树链剖分有了一定的理解.

再次,祝愿各位巨佬们,拿到心仪的大厂offer,年薪天天往上涨,职位不停往上飞,编程水平迅速提高,脱单顺利且幸福.

概念	定义
重儿子(节点)	父亲节点的所有儿子中子树结点数目最多的结点；
轻儿子(节点)	父亲节点中除了重儿子以外的所有儿子节点
重边(一条边)	父亲结点和重儿子连成的边
轻边(一条边)	父亲节点和轻儿子连成的边
重链(多条边)	由多条重边连接而成的路径
轻链(多条边)	由多条轻边连接而成的路径

概念理解了,那么算法其实也就不难理解了.

其实树链剖分只是一个思想,所以我们把思想牢记于心,那么就不难.

学好算法,一定不要畏难,面对大量的知识,秦淮岸只能尽量浅显易懂地解释,所以希望大家停留在上面的表格一分钟,牢记于心.

---

算法梳理

我们认真审核一下树链剖分算法,理解一下树链剖分到底是要做什么,怎么处理,代码写法是什么啊,这样处理有什么好处,它的特点是什么.

树链剖分要做些什么

树链剖分,闻其名,通其意.就是把一棵树划分成几条链.

现实理解:

Acwing1班开学了,Acwing的同学们,他们互相的关系,组成一个关系树,然后我们安排座位,分成不同的小组.

提示:关系树其实一颗树,而每一个小组其实就是一条链.

怎么处理

重新编号

咱们知道,一个班级的管理,是有很多编排方式,但是最常见的方式,就是学号编排.

所以为了更好的管理一个班级,为什么不使用学号编排呢.

因此咱们使用学号编排,不过呢这个学号编排有独特之处.

小A请默认是自己.

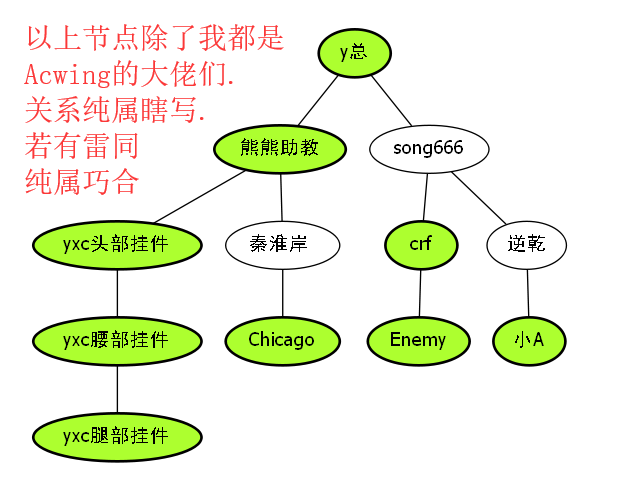
加入现在操场上,所有人按照以上顺序站着,然后y总拿着达达牌小橙笔,开始了标记学号.

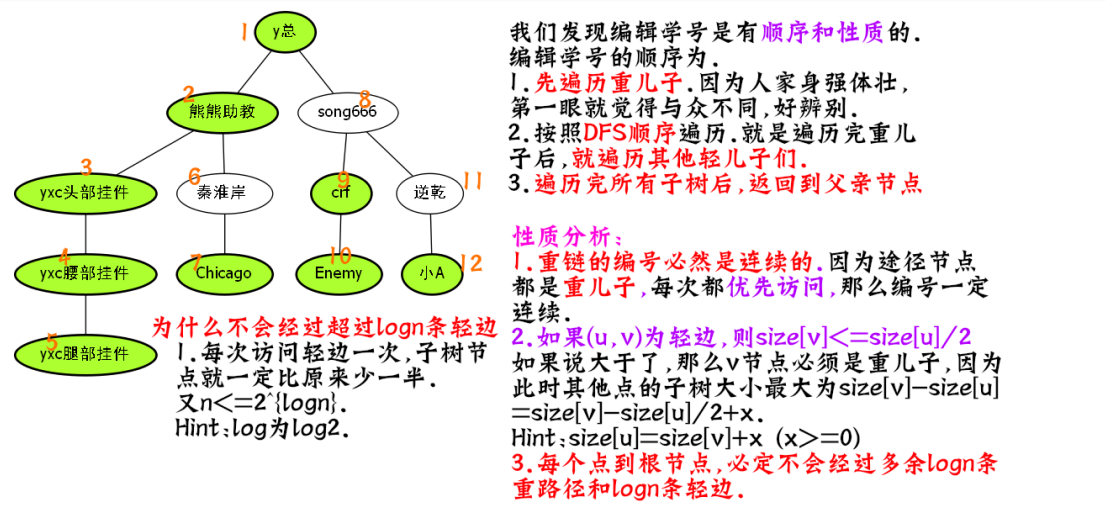
以上这张图片,非常重要,如果不懂,一定要看蒟蒻的直播讲解.广告时间到了

现在学号编辑完毕了,那么现在的重点,就是分小组了.

分类小组

咱们知道一个小组,肯定有一个核心人物红太阳.

那么谁是咱们的红太阳,红太阳肯定走在最前面,迎接着晨曦.

所以一个小组的组长红太阳,一定是一条链的链头.

对于重链而言,他的链头,一定就是深度最浅的那一位.

不然肯定有人玩着篮球踩在它的头上.

对于轻链而言,他的链头,就是他自己,毕竟是孤寡老人.

总结讨论

总结一下,我们需要哪些元素.

1. 深度(为了下面服务)
2. 父亲节点
3. 子树大小(团队大小)
4. 重儿子(身宽体胖)
5. DFS序(新学号)
6. 链顶(红太阳)
7. 老编号(曾经的编号,其实就是名字,毕竟A遇到B,总不能一直喊人家叫做XX号)

一个表格设置一下.

定义	含义
\(deep[x]\)	节点\(x\)的深度
\(fa[x]\)	节点\(x\)的父亲
\(size[x]\)	节点\(x\)的子树大小
\(wson[x]\)	节点\(x\)的重儿子的老编号(名字).
\(dfn[x]\)	节点\(x\)的新编号,其实也就是DFS序
\(top[x]\)	节点\(x\)所在链的链头
\(pre[x]\)	节点\(x\)的老编号,也就是老名字.

总而言之,这就是我们的目标数组了,看上去好多啊,但其实只要两次DFS就解决完毕了.

---

代码解析

void dfs1(int x,int father)//father是x的父亲节点
{
	size[x]=1;//刚开始子树为1,也就是直接
	for(int i=head[x]; i; i=Next[i])//访问所有出边
	{
		int y=edge[i];//儿子节点
		if (y==father)//访问到唯一一个不是儿子节点的父亲节点去了
			continue;//当然不可以,直接跳过
		deep[y]=deep[x]+1;//深度+1,儿子节点是父亲节点深度+1
		fa[y]=x;//y的父亲节点是x
		dfs1(y,x);//y的父亲节点是x
		size[x]+=size[y];//加上儿子贡献的子树
		if (size[y]>size[wson[x]])//如果这个节点比当前重儿子,子树还要多(还要重) ,那么营养过剩的重儿子就是他了.
			wson[x]=y;//wson[x]表示x节点的重儿子
	}
}

这一层DFS,就让我们求解出来了前四个数组,那么后三个数组呢?

void dfs2(int x,int tp)//x表示当前节点,tp表示链头
{
	dfn[x]=++cnt;//重新编辑编号
	pre[cnt]=x;//存储老编号
	top[x]=tp;//存储链头
	if (wson[x]) //优先处理重儿子
		dfs2(wson[x],tp);
	for(int i=head[x]; i; i=Next[i])//访问所有的轻链
	{
		int y=edge[i];//存储出边
		if (y==wson[x] || y==fa[x])//重儿子已经处理过了,父亲节点不可以抵达
			continue;
		dfs2(y,y);//每一个轻链的链头,都是自己,而且重儿子的开头都是轻链.
	}
}

---

算法拓展

咱们知道,树链剖分是LCA+树上差分的合并增强版,那么他们两个有的操作,他当然也得有.

正如同某名言.你的是我的,我的还是我的.

先来看LCA的操作,其实就是其名的求两点的最近公共祖先.

我们对于上面所述的top数组,也就是链头数组,比较懵逼,觉得他似乎没有什么用处啊.

实际上它的用处非常之大,是树链剖分的核心数组之一.

通俗理解的故事,又来了.以下内容纯属瞎编,只为了更好的理解.

\(Acwing\)学校开课了,孩子算法学不好,怎么办?

多半是找不到好老师,快来参加\(Acwing\)算法实验班.

现在知道\(Acwing\)学校里面实力最为高深莫测就是y总,但是不是所有人都认识y总.

现在小\(A\)同学想知道自己学校的校长是谁,但是他是新来的新生.

1. 小\(A\)同学只认识自己的组长\(song666\)巨佬.

2. \(song666\)巨佬只知道年级组长\(Acwing1901\)班的熊熊老师.

3. 熊熊老师知道y总,所以咱们得出了以下这条最短路径.

\[小A->song666->Acwing1901班熊熊老师->y总 \]

如果说所有人都不会树链剖分算法的top链头数组,那么将会这样询问.

我们假设熊熊老师是年级组长.(原谅我只认识熊熊老师)

\[小A->小B->小C->小D->song666巨佬-> \\\\ Acwing1905班主任媛媛老师->Acwing1904班丰丰老师->Acwing1903班辰辰老师 \\\\ ->Acwing1902班彬彬老师->Acwing1901班熊熊年级组长->y校长. \]

我们发现链头数组,其实可以形象的认为,一个小组的领头人物.

重点来了,注意力迅速集中.

假如说节点A在A小组,然后节点B在B小组,要我们找\(Lca(a,b)\).

那么我们得出.

因为A小组和B小组是两个没有交集的小组.(也就是互相都不认识)

那么显然A小组这一串人,都不可能成为答案.

同理B小组这一伙人,也不可能成为答案.

明知没有用,何必浪费时间.

所以,我们迅速跨越中间的所有节点.

a=top[a];//直接爬到链头
b=top[b];//直接爬到链头

这样我们发现效率直线上升.

\[本来我们a节点爬到这条链需要花费O(len(a)). \]

提示一下

\[提示:len(a)表示这条a所在链的长度. \]

但是现在得了链头点,一个传染两.

于是时间效率突飞猛进.

\[O(1) \]

这就是树链剖分的完美之处.

然后我们知道从任意一个节点,抵达根节点的链数量,不会超过\(O(logn)\)条重链,和\(O(logn)\)条轻链.

因此我们查询复杂度的极限是.

\[O(log^2n) \]

看上去比Lca差一些啊,倍增Lca查询的时间复杂度是\(O(logn)\)

事实上很多时候复杂度小的可怜,比如说.

假如说A和B在同一个小组,而且B是组长,那么复杂度\(O(1)\)

注意点

还有请注意,每次跳跃的话.
比如说a,b节点要跳跃.
我们每次是将链头深度深的节点往上跳跃,而不本节点的深度.
为了避免出现下面评论所说的情况.
两个节点,跳过去了,跳到了LCA节点的上方去了.

拓展代码

int Query_sum(int a,int b)//a,b这条路径上的权值和
{
	int ans=0;//初始化为0
	while(top[a]!=top[b]) //此时a,b不在同一条重链上面
	{
		if (deep[top[a]]<deep[top[b]])//我们这里默认a是深度在下面的链
			swap(a,b);
		ans+=t.Query_sum(1,1,n,dfn[top[a]],dfn[a]);//访问这条重链,dfn[top[a]]是链头,dfn[a]是当前节点,dfn[top[a]]<dfn[a]因为a后访问.
		a=fa[top[a]];//往上面访问,也就是往上面爬一步
	}
	if (deep[a]<deep[b])//保证a深度比b深度,深.保证后面查询l<r
		swap(a,b);
	ans+=t.Query_sum(1,1,n,dfn[b],dfn[a]);//他们已经在同一条重链上面了
	return ans;
}

链上结构

路径操作

看到上面的代码,我们发现t是什么东西.

t其实就是我们的线段树数据结构.

根据树上差分的操作们,得知我们的树链剖分需要复制一大波操作.

1. 将树从x到y结点最短路径上所有节点的值都加上z

2. 求树从x到y结点最短路径上所有节点的值之和

根据上面这些操作,我们不难发现,每条链也需要资瓷这些操作.

综上所述得出.

1. 一条链上,需要资瓷区间修改.
2. 一条链上,需要支持区间查询.

总而言之,区间操作多多,因此我们使用线段树.

当然了巨佬们,肯定喜欢使用平衡树等等高大上,上档次,有内涵的数据结构,但是线段树的代码复杂度对于考试而言,是最好不过的结构了.

代码复杂度是考试的时候,极为重要的复杂度. by Acwing站长,校长,集训队大佬yxc总裁

总而言之,言而总之,我们树链剖分的代码量,成功的增加了1k.

子树操作

我们再来几个操作.

1. 将以x为根节点的子树内所有节点值都加上z

2. 求以x为根节点的子树内所有节点值之和

看到子树操作,有点不知所措,线段树似乎不支持这个鬼东西吧,难道代码量又要翻倍处理.

事实上,我们的代码只需要增加八行代码,也就核心两句话.

我们的DFS遍历,在这里起到了决定性,关键性,核心性的作用.(语文老师:捕捉到了病句,起到了,什么的作用,句式杂糅)

我们发现DFS序列的一个重点,就是.一颗子树,它的DFS序,是有序的.

还是这张图,我们发现熊熊助教这颗子树.

其实就是\([2,7]\)的这个区间.

因此我们只要修改\([2,7]\)这个区间,就达到了修改以2为根的树修改.

因此代码如下.

void Update(int x,int v)//修改子树的值
{
	t1.Update(1,1,n,dfn[x],dfn[x]+size[x]-1,v);//DFS序是有序的数列
}

同理,查询操作也就如下所示了.

int Query_sum(int x)//查询子树的和
{
	return t1.Query_sum(1,1,n,dfn[x],dfn[x]+size[x]-1);//统计子树和,其实和修改差不多
}

树链模板

struct line_tree//线段树
{
#define mid (l+r>>1)//二分中点 
#define Lson (rt<<1),l,mid//左儿子 
#define Rson (rt<<1 | 1),mid+1,r//右儿子 
#define Len (r-l+1)//区间长度
	void Push_down(int rt,int l,int r)
	//这里的懒惰标记只适合区间修改,把[l,r]区间都变成v.如果是都+v,则必须Lazy标记+=,而不是下面的=
	{
		if (Lazy[rt]!=-1)//当前节点有Lazy标记
		{
			Lazy[rt<<1]=Lazy[rt<<1 | 1]=Lazy[rt];//懒惰标记下传
			sum[rt<<1]=Lazy[rt]*(mid-l+1);//左儿子的区间长度
			sum[rt<<1 |1]=Lazy[rt]*(r-(mid+1)+1);//右儿子的区间长度
			Lazy[rt]=-1;//此时懒惰标记已经下传完毕了,那么可以全部清空了
		}
	}
	void build(int rt,int l,int r)
	{
		Lazy[rt]=-1;
		if (l==r)//叶子节点
		{
			sum[rt]=1;//sum数组
			return ;
		}
		build(Lson);//左儿子
		build(Rson);//右儿子
		sum[rt]=sum[rt<<1]+sum[rt<<1 |1];//左儿子节点+右儿子节点
	}
	void Update(int rt,int l,int r,int L,int R,int v)//将[L,R]区间统统修改成为v,然后当前区间[l,r]
	{
		if (L<=l && r<=R)//当前区间被包括了
		{
			Lazy[rt]=v;//懒惰标记修改
			sum[rt]=v*Len;//全部修改完毕
			return ;
		}
		Push_down(rt,l,r);//向下传递Lazy标记
		if (L<=mid)//在左儿子身上
			Update(Lson,L,R,v);//左儿子
		if (R>mid)//在右儿子身上
			Update(Rson,L,R,v);//右儿子
		sum[rt]=sum[rt<<1]+sum[rt<<1 |1];//左儿子+右儿子
	}
	int Query_sum(int rt,int l,int r,int L,int R)//查询[L,R]区间和,当前区间[l,r]
	{
		int ans=0;
		if (L<=l && r<=R)//当前区间被包括了
			return sum[rt];
		if (L<=mid)//左儿子上面
			ans+=Query_sum(Lson,L,R);
		if (R>mid)//右儿子上面
			ans+=Query_sum(Rson,L,R);
		sum[rt]=sum[rt>>1]+sum[rt>>1 |1];
		return ans;//返回
	}
} t1;
struct Tree_Chain//树链剖分
{
	void add_edge(int a,int b)//添加边函数
	{
		edge[++tot]=b;//出边节点
		Next[tot]=head[a];//链表链接
		head[a]=tot;//上一个节点
	}
	void dfs1(int x,int father)//x节点,和他的父亲节点father
	{
		size[x]=1;//刚开始就自己这一个节点
		for(int i=head[x]; i; i=Next[i]) //开始遍历所有的出边
		{
			int y=edge[i];//出边节点
			if (y==father)//儿子节点是不可以等于父亲节点的
				continue;
			deep[y]=deep[x]+1;//儿子的深度,是父亲深度+1
			fa[y]=x;//y的父亲节点是x
			dfs1(y,x); //开始遍历儿子节点
			size[x]+=size[y];//儿子节点贡献子树大小
			if (size[y]>size[wson[x]]) //发现当前的儿子节点,比之前的重儿子,还要重(胖),那么更新重儿子
				wson[x]=y;//更新
		}
		return ;//华丽结束
	}
	void dfs2(int x,int tp)//x节点,以及x节点所在链的链头
	{
		dfn[x]=++cnt;//当前节点的新编号,也就是DFS序编号
		pre[cnt]=x;//老编号,虽然在整道题目中没有用处,但是树链剖分板子打一遍也是好的
		top[x]=tp;//链头存储一下
		if (wson[x])//有重儿子,那么一定先访问重儿子
			dfs2(wson[x],tp); //访问节点,此时重儿子一定在重链上,所以还是tp
		for(int i=head[x]; i; i=Next[i]) //访问所有的轻儿子
		{
			int y=edge[i];//出边
			if (y==wson[x] || y==fa[x])//轻儿子节点不能是重儿子,也不能是父亲节点
				continue;
			dfs2(y,y);//每一个轻儿子,他的链头其实都是自己,而且重链的开头也得是轻儿子
		}
	}
	void Update(int x,int v)//修改子树的值
	{
		t1.Update(1,1,n,dfn[x],dfn[x]+size[x]-1,v);//DFS序是有序的数列
	}
	int Query_sum(int x)//查询子树的和
	{
		return t1.Query_sum(1,1,n,dfn[x],dfn[x]+size[x]-1);//统计子树和,其实和修改差不多
	}
	long long Query_sum2(int a,int b)//a,b这条路径上的权值和
	{
		long long ans=0;//初始化为0
		while(top[a]!=top[b]) //此时a,b不在同一条重链上面
		{
			if (deep[top[a]]<deep[top[b]])//我们这里默认a是深度在下面的链
				swap(a,b);
			now_ans=0;
			t1.Query_sum(1,1,n,dfn[top[a]],dfn[a]);
			ans+=now_ans;//访问这条重链,dfn[top[a]]是链头,dfn[a]是当前节点,dfn[top[a]]<dfn[a]因为a后访问.
			a=fa[top[a]];//往上面访问,也就是往上面爬一步
		}
		if (deep[a]<deep[b])//保证a深度比b深度,深.保证后面查询l<r
			swap(a,b);
		now_ans=0;
		t1.Query_sum(1,1,n,dfn[top[a]],dfn[a]);
		ans+=now_ans;//他们已经在同一条重链上面了
		return ans;
	}
    int Update2(int a,int b) //链上修改 
    {
        while(top[a]!=top[b])//也就是两个点还在不同的重链上
        {
            if (deep[top[a]]<deep[top[b]])//我们默认a节点是深度比b节点深一些
                swap(a,b);//交换一下就好了
            t1.Update(1,1,n,dfn[top[a]],dfn[a],0);//在爬的过程中,也帮忙修改一下
            a=fa[top[a]];//往上面爬一下
        }
        if (deep[a]<deep[b])//保证a深度比b深度,深.保证后面查询l<r
            swap(a,b);
        t1.Update(1,1,n,dfn[b],dfn[a],0);//同一条链了,那么修改这条链上在[a,b]之间的点 
    }
    //请注意,本模板是很多题目的操作合并而成,可能有问题,但是单独没有问题.如果有问题请艾特博主.
    //所有代码风格为博主风格,所以操作之间都是通用的,应该不会出现问题.
} t2;

经典选讲

第一题 模板题[HAOI2015]树上操作

题目描述

有一棵点数为 \(N\) 的树，以点 \(1\) 为根，且树点有边权。然后有 \(M\) 个操作，分为三种：

• 操作 1 ：把某个节点 \(x\) 的点权增加 \(a\) 。
• 操作 2 ：把某个节点 \(x\) 为根的子树中所有点的点权都增加 \(a\)。
• 操作 3 ：询问某个节点 \(x\) 到根的路径中所有点的点权和。

输入输出格式

输入格式：

第一行包含两个整数 \(N, M\) 。表示点数和操作数。
接下来一行 \(N\) 个整数，表示树中节点的初始权值。
接下来 \(N-1\) 行每行两个正整数 \(from\), \(to\) ， 表示该树中存在一条边 \((from, to)\) 。
再接下来 \(M\) 行，每行分别表示一次操作。其中第一个数表示该操作的种类\(（ 1-3 ）\) ，之后接这个操作的参数（ x 或者 x a ） 。

输出格式：

对于每个询问操作，输出该询问的答案。答案之间用换行隔开。

输入输出样例

输入样例#1：

5 5
1 2 3 4 5
1 2
1 4
2 3
2 5
3 3
1 2 1
3 5
2 1 2
3 3

输出样例#1：

6
9
13

数据范围

对于 \(100%\) 的数据， \(N,M \le 100000\) ，且所有输入数据的绝对值都不会超过 \(10^6\) 。

题意理解

一棵树上,要求支持单点修改,子树修改,路径修改操作.

思路解析

学会了树连剖分的我们,很轻松的发现,这就是一个树链剖分的模板题目.

所以说,我们几乎是可以轻松解决这道题目了.

树链剖分超级详解,可以媲美全网第一通俗树链剖分讲解了

于是我们惊奇的发现一道省选题目,就这样轻松愉快地AC了.

代码超多中文解释,绝对看得懂.

代码解析

#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+200;
int sum[N<<2],Lazy[N<<2];//处理区间和;懒惰标记
int head[N<<1],edge[N<<1],ver[N<<1],Next[N<<1],tot;
int pre[N],deep[N],size[N],a[N],fa[N],cnt;
int wson[N],dfn[N],top[N],n,m,now_ans;
struct line_tree
{
#define mid ((l+r)>>1) //二分值 
#define lson root<<1,l,mid //左儿子 
#define rson root<<1|1,mid+1,r //右儿子 
#define len (r-l+1) //区间长度 
	void build(int root,int l,int r)
	{
		if (l==r)//抵达叶子节点,也就是单个节点
		{
			sum[root]=a[pre[l]];
			return ;
		}
		build(root<<1,l,mid);//左儿子
		build(root<<1 | 1,mid+1,r);//右儿子
		sum[root]=sum[root<<1]+sum[root<<1 | 1];//左右儿子都访问完毕了,可以更新父亲节点了.
	}
	inline void Push_down(int x,int lenn)
	{
		Lazy[x<<1]+=Lazy[x];//左儿子得到,父亲节点的懒惰标记下传
		Lazy[x<<1 | 1]+=Lazy[x];//右儿子得到,父亲节点的懒惰标记下传
		sum[x<<1]+=Lazy[x]*(lenn-(lenn>>1));//懒惰标记的值叠加
		sum[x<<1 | 1]+=Lazy[x]*(lenn>>1);//懒惰标记的值叠加
		Lazy[x]=0;//懒惰标记已经下传
	}
	inline void Query_sum(int root,int l,int r,int L,int R)//目标区间ql,qr,当前区间[l,r],当前节点是root
	{
		if(L<=l&&r<=R)//目标区间包含了当前区间
		{
			now_ans+=sum[root];//累加
			return;//返回
		}
		else
		{
			if(Lazy[root])//有标记
				Push_down(root,len);//先走标记
			if(L<=mid)//左儿子上有
				Query_sum(lson,L,R);
			if(R>mid)//右儿子上
				Query_sum(rson,L,R);
		}
	}
	inline void Update(int root,int l,int r,int L,int R,int k)//目标区间[L,R]全部要加上K,当前区间[l,r]
	{
		if (L<=l && r<=R)//[L,R]包括了当前区间[l,r]
		{
			Lazy[root]+=k;//叠加懒惰标记
			sum[root]+=k*len;
			return ;
		}
		if (Lazy[root])//有懒惰标记
			Push_down(root,len);//下传标记
		if (L<=mid)
			Update(lson,L,R,k);//左儿子
		if (R>mid)
			Update(rson,L,R,k);//右儿子
		sum[root]=sum[root<<1]+sum[root<<1 |1];
	}
} t1;
struct Tree_Chain
{
	inline void add_edge(int a,int b)
	{
		edge[++tot]=b;
		Next[tot]=head[a];
		head[a]=tot;
	}
	void dfs1(int x,int father)//fa是x的父亲节点
	{
		size[x]=1;//刚开始子树为1,也就是直接
		for(int i=head[x]; i; i=Next[i])//访问所有出边
		{
			int y=edge[i];//儿子节点
			if (y==father)//访问到唯一一个不是儿子节点的父亲节点去了
				continue;//当然不可以,直接跳过
			deep[y]=deep[x]+1;//深度+1,儿子节点是父亲节点深度+1
			fa[y]=x;//y的父亲节点是x
			dfs1(y,x);//y的父亲节点是x
			size[x]+=size[y];//加上儿子贡献的子树
			if (size[y]>size[wson[x]])//如果这个节点比当前重儿子,子树还要多(还要重) ,那么营养过剩的重儿子就是他了.
				wson[x]=y;//wson[x]表示x节点的重儿子
		}
	}
	void dfs2(int x,int tp)//x表示当前节点,tp表示链头
	{
		dfn[x]=++cnt;//重新编辑编号
		pre[cnt]=x;//存储老编号
		top[x]=tp;//存储链头
		if (wson[x]) //优先处理重儿子
			dfs2(wson[x],tp);
		for(int i=head[x]; i; i=Next[i])//访问所有的轻链
		{
			int y=edge[i];//存储出边
			if (y==wson[x] || y==fa[x])//重儿子已经处理过了,父亲节点不可以抵达
				continue;
			dfs2(y,y);//每一个轻链的链头,都是自己,而且重儿子的开头都是轻链.
		}
	}
	long long Query_sum(int a,int b)//a,b这条路径上的权值和
	{
		long long ans=0;//初始化为0
		while(top[a]!=top[b]) //此时a,b不在同一条重链上面
		{
			if (deep[top[a]]<deep[top[b]])//我们这里默认a是深度在下面的链
				swap(a,b);
			now_ans=0;
			t1.Query_sum(1,1,n,dfn[top[a]],dfn[a]);
			ans+=now_ans;//访问这条重链,dfn[top[a]]是链头,dfn[a]是当前节点,dfn[top[a]]<dfn[a]因为a后访问.
			a=fa[top[a]];//往上面访问,也就是往上面爬一步
		}
		if (deep[a]<deep[b])//保证a深度比b深度,深.保证后面查询l<r
			swap(a,b);
		now_ans=0;
		t1.Query_sum(1,1,n,dfn[top[a]],dfn[a]);
		ans+=now_ans;//他们已经在同一条重链上面了
		return ans;
	}
	inline void update_son(int x,int k)
	{
		t1.Update(1,1,n,dfn[x],dfn[x]+size[x]-1,k);
		//因为DFS所以子树其实是有序的,而且一个子树大小是size[x],那么dfn+size-1就可以遍历整棵树
	}
} t2;
signed main()//其实就是int main()
{
//	freopen("stdin.in","r",stdin);
//	freopen("a.out","w",stdout);
	scanf("%lld%lld",&n,&m);
	for(int i=1; i<=n; i++)
		scanf("%lld",&a[i]);
	for(int i=1; i<n; i++)
	{
		int a,b;
		scanf("%lld%lld",&a,&b);
		t2.add_edge(a,b);
		t2.add_edge(b,a);//无向图建立边
	}
	t2.dfs1(1,0);//第一次DFS,求size,deep,fa
	t2.dfs2(1,1);//第二DFS求dfn,top
	t1.build(1,1,n);
	while(m--)
	{
		int k,a,b,c;
		scanf("%lld",&k);
		if (k==1)
		{
			scanf("%lld%lld",&a,&b);
			t1.Update(1,1,n,dfn[a],dfn[a],b);//虽然是区间修改[dfn[a],dfn[a]],但是其实是单点修改.
		}
		if (k==2)
		{
			scanf("%lld%lld",&a,&b);
			t2.update_son(a,b);//修改a以及子树,统统增加b
		}
		if (k==3)
		{
			scanf("%lld",&a);
			printf("%lld\n",t2.Query_sum(1,a));
		}
	}
	return 0;
}

第二题 [NOI2015]软件包管理器

不知道各位发现这道题目莫名的和楼上这道题目竟然惊奇地年份吻合,难度吻合,算法吻合,于是题目也就基本上吻合了.

不知道河南的队爷们是否要感谢毒瘤出题人的精彩押题呢....

题目描述

Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器，你可以通过一行命令安装某一个软件包，然后软件包管理器会帮助你从软件源下载软件包，同时自动解决所有的依赖（即下载安装这个软件包的安装所依赖的其它软件包），完成所有的配置。Debian/Ubuntu使用的apt-get，Fedora/CentOS使用的yum，以及OSX下可用的homebrew都是优秀的软件包管理器。

你决定设计你自己的软件包管理器。不可避免地，你要解决软件包之间的依赖问题。如果软件包A依赖软件包B，那么安装软件包A以前，必须先安装软件包B。同时，如果想要卸载软件包B，则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且，由于你之前的工作，除0号软件包以外，在你的管理器当中的软件包都会依赖一个且仅一个软件包，而0号软件包不依赖任何一个软件包。依赖关系不存在环（若有\(m(m \le 2)\)个软件包\(A_1,A_2,A_3,⋯,A_m\)，其中\(A_1\)依赖\(A_2\)，\(A_2\)依赖\(A_3\)，\(A_3\)依赖\(A_4，……，A_{m-1}\)依赖\(A_m\)，而\(A_m\)依赖#A_1$，则称这m个软件包的依赖关系构成环），当然也不会有一个软件包依赖自己。

现在你要为你的软件包管理器写一个依赖解决程序。根据反馈，用户希望在安装和卸载某个软件包时，快速地知道这个操作实际上会改变多少个软件包的安装状态（即安装操作会安装多少个未安装的软件包，或卸载操作会卸载多少个已安装的软件包），你的任务就是实现这个部分。注意，安装一个已安装的软件包，或卸载一个未安装的软件包，都不会改变任何软件包的安装状态，即在此情况下，改变安装状态的软件包数为0。

输入输出格式

输入格式：

输入文件的第1行包含1个整数n，表示软件包的总数。软件包从0开始编号。

随后一行包含n−1个整数，相邻整数之间用单个空格隔开，分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。

接下来一行包含1个整数q，表示询问的总数。之后q行，每行1个询问。询问分为两种：

install x：表示安装软件包x

uninstall x：表示卸载软件包x

你需要维护每个软件包的安装状态，一开始所有的软件包都处于未安装状态。

对于每个操作，你需要输出这步操作会改变多少个软件包的安装状态，随后应用这个操作（即改变你维护的安装状态）。

输出格式：

输出文件包括q行。

输出文件的第i行输出1个整数，为第i步操作中改变安装状态的软件包数。

输入输出样例

输入样例#1：

7
0 0 0 1 1 5
5
install 5
install 6
uninstall 1
install 4
uninstall 0

输出样例#1：

3
1
3
2
3

输入样例#2：

10
0 1 2 1 3 0 0 3 2
10
install 0
install 3
uninstall 2
install 7
install 5
install 9
uninstall 9
install 4
install 1
install 9

输出样例#2：

1
3
2
1
3
1
1
1
0
1

说明

【样例说明 1】

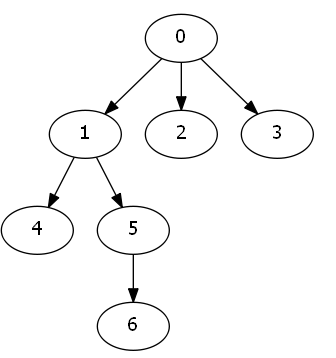
一开始所有的软件包都处于未安装状态。

安装\(5\)号软件包，需要安装\(0,1,5\)三个软件包。

之后安装\(6\)号软件包，只需要安装\(6\)号软件包。此时安装了\(0,1,5,6\)四个软件包。

卸载\(1\)号软件包需要卸载\(1,5,6\)三个软件包。此时只有\(0\)号软件包还处于安装状态。

之后安装\(4\)号软件包，需要安装\(1,4\)两个软件包。此时\(0,1,4\)处在安装状态。最后，卸载0号软件包会卸载所有的软件包。

数据范围

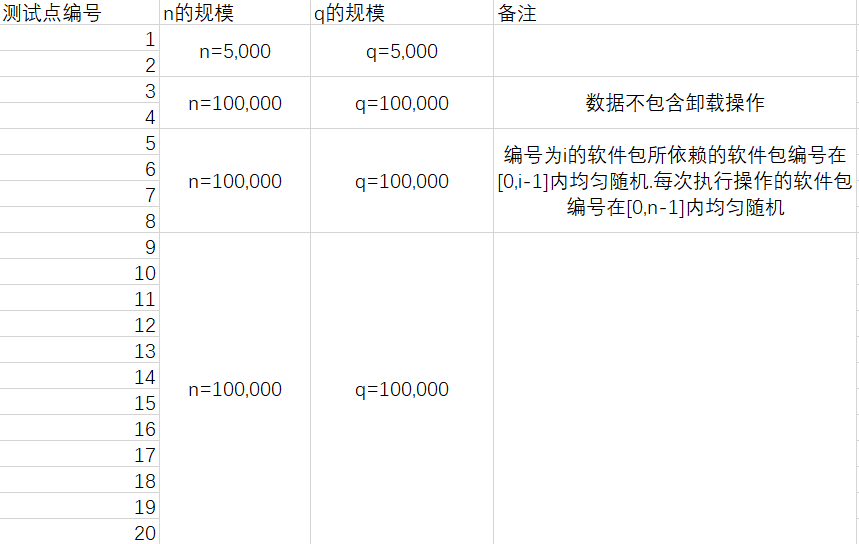
测试点编号	n的规模	q的规模	备注
1	\(n=5,000\)	\(q=5,000\)
2	\(n=5,000\)	\(q=5,000\)
3	\(n=100,000\)	\(q=100,000\)	数据不包含卸载操作
4	\(n=100,000\)	\(q=100,000\)	数据不包含卸载操作
5	\(n=100,000\)	\(q=100,000\)	编号为\(i\)的软件包所依赖的软件包编号在\([0,i-1]\)内均匀随机.每次执行操作的软件包编号在\([0,n-1]\)内均匀随机
6	\(n=100,000\)	\(q=100,000\)	编号为\(i\)的软件包所依赖的软件包编号在\([0,i-1]\)内均匀随机.每次执行操作的软件包编号在\([0,n-1]\)内均匀随机
7	\(n=100,000\)	\(q=100,000\)	编号为\(i\)的软件包所依赖的软件包编号在\([0,i-1]\)内均匀随机.每次执行操作的软件包编号在\([0,n-1]\)内均匀随机
8	\(n=100,000\)	\(q=100,000\)	编号为\(i\)的软件包所依赖的软件包编号在\([0,i-1]\)内均匀随机.每次执行操作的软件包编号在\([0,n-1]\)内均匀随机
9	\(n=100,000\)	\(q=100,000\)
10	\(n=100,000\)	\(q=100,000\)
11	\(n=100,000\)	\(q=100,000\)
12	\(n=100,000\)	\(q=100,000\)
13	\(n=100,000\)	\(q=100,000\)
14	\(n=100,000\)	\(q=100,000\)
15	\(n=100,000\)	\(q=100,000\)
16	\(n=100,000\)	\(q=100,000\)
17	\(n=100,000\)	\(q=100,000\)
18	\(n=100,000\)	\(q=100,000\)
19	\(n=100,000\)	\(q=100,000\)
20	\(n=100,000\)	\(q=100,000\)