NOIP2016 Day1 T2 天天爱跑步(树上差分,LCA)
题目描述
小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 \(n\)个结点和 \(n-1\)条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从\(1\)到\(n\)的连续正整数。
现在有\(m\)个玩家,第\(i\)个玩家的起点为 \(S_i\),终点为 \(T_i\) 。每天打卡任务开始时,所有玩家在第\(0\)秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小c想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点\(j\)的观察员会选择在第\(W_j\)秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第\(W_j\)秒也理到达了结点 \(j\) 。 小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点\(j\)作为终点的玩家: 若他在第\(W_j\)秒前到达终点,则在结点\(j\)的观察员不能观察到该玩家;若他正好在第\(W_j\)秒到达终点,则在结点\(j\)的观察员可以观察到这个玩家。
输入输出格式
输入格式：
第一行有两个整数\(n\)和\(m\) 。其中\(n\)代表树的结点数量, 同时也是观察员的数量, \(m\)代表玩家的数量。
接下来 \(n- 1\)行每行两个整数\(u\)和 \(v\),表示结点 \(u\)到结点 \(v\)有一条边。
接下来一行 \(n\)个整数,其中第\(j\)个整数为\(W_j\) , 表示结点\(j\)出现观察员的时间。
接下来 \(m\)行,每行两个整数\(S_i\),和\(T_i\),表示一个玩家的起点和终点。
对于所有的数据,保证\(1\leq S_i,T_i\leq n, 0\leq W_j\leq n\) 。
输出格式：
输出1行 \(n\)个整数,第\(j\)个整数表示结点\(j\)的观察员可以观察到多少人。
输入输出样例
输入样例#1：
6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6
输出样例#1：
2 0 0 1 1 1
输入样例#2：
5 3
1 2
2 3
2 4
1 5
0 1 0 3 0
3 1
1 4
5 5
输出样例#2：
1 2 1 0 1
说明
【样例1说明】
对于\(1\)号点，\(W_i=0\)，故只有起点为1号点的玩家才会被观察到，所以玩家\(1\)和玩家\(2\)被观察到，共有\(2\)人被观察到。
对于\(2\)号点，没有玩家在第\(2\)秒时在此结点，共\(0\)人被观察到。
对于\(3\)号点，没有玩家在第\(5\)秒时在此结点，共\(0\)人被观察到。
对于\(4\)号点，玩家\(1\)被观察到，共\(1\)人被观察到。
对于\(5\)号点，玩家\(1\)被观察到，共\(1\)人被观察到。
对于\(6\)号点，玩家\(3\)被观察到，共\(1\)人被观察到。
【子任务】
每个测试点的数据规模及特点如下表所示。 提示: 数据范围的个位上的数字可以帮助判断是哪一种数据类型。
【提示】
如果你的程序需要用到较大的栈空问 (这通常意味着需要较深层数的递归), 请务必仔细阅读选手日录下的文本当rumung:/stact.p″, 以了解在最终评测时栈空问的限制与在当前工作环境下调整栈空问限制的方法。
在最终评测时，调用栈占用的空间大小不会有单独的限制，但在我们的工作环境中默认会有 8 MB8M**B 的限制。 这可能会引起函数调用层数较多时， 程序发生栈溢出崩溃。
我们可以使用一些方法修改调用栈的大小限制。 例如， 在终端中输入下列命令 ulimit -s 1048576
此命令的意义是，将调用栈的大小限制修改为 1 GB1G**B。
例如，在选手目录建立如下 sample.cpp 或 sample.pas
将上述源代码编译为可执行文件 sample 后，可以在终端中运行如下命令运行该程序
./sample
如果在没有使用命令“ ulimit -s 1048576”的情况下运行该程序， sample会因为栈溢出而崩溃； 如果使用了上述命令后运行该程序，该程序则不会崩溃。
特别地， 当你打开多个终端时， 它们并不会共享该命令， 你需要分别对它们运行该命令。
请注意， 调用栈占用的空间会计入总空间占用中， 和程序其他部分占用的内存共同受到内存限制。
解题报告
题意理解
在一棵\(n-1\)个节点的树上,有\(m\)个人,他们会从\(s_i\)走到\(t_i\),然后每走一条边都要花费\(1\)个时间.
树上有\(n\)个观察员,第\(i\)个观察员,会在\(w_i\)时间出现,然后一直观察着人.
一个人可以被第\(i\)观察员看到,必须满足以下条件.
- 抵达这个节点的时间\(\ge\)第\(i\)观察员出现的时间\(w_i\)
- 这个人会经过第\(i\)观察员出现的节点.
算法解析
简化题意
贡献转移
其实每一个人的行程,可以看作对路程上节点们的贡献.
.PNG)
通过特例看通项,由点到面,是数学思想,同时也是我们推出性质的好帮手.
推导性质
题意分析
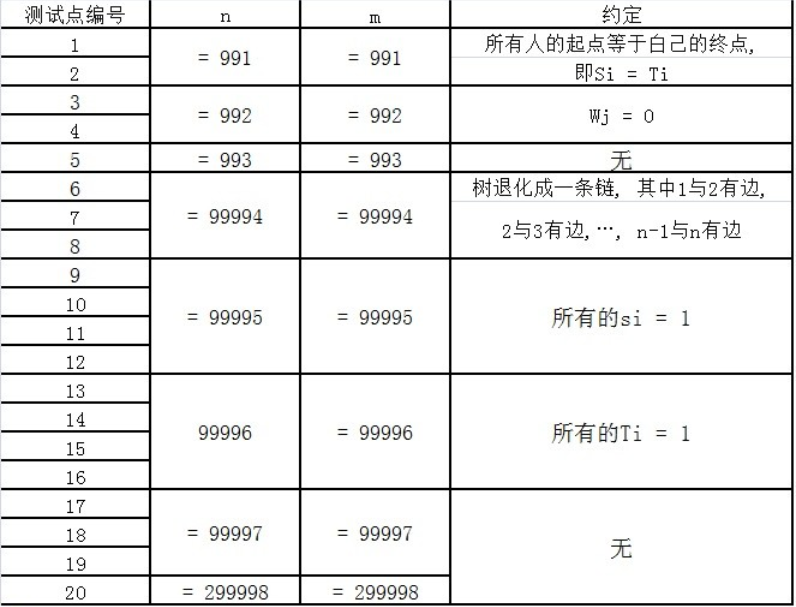
我们通过上面这张图,可以得到很多性质.
- 起点到终点的路径,只有一条.
- 在起点\(S_i\)到终点\(T_i\)的过程,会在\(Lca(S_i,T_i)\)这个节点,发生转折.
- 我们可以将一条路径,剖分成为两条链.而剖分的地方,就是我们的\(Lca(S_i,T_i)\)
根据上面这张图,以及我们的性质3,我们可以将图片变成如下所示.
.PNG)
我们成功地将一条路径,变成了两条链.
我们来分类讨论一下这两条链.
上升链
- 对于橙色链而言.
我们现在最为迫切地就是想要知道,每一个花痴观察员,他到底可以看到多少个仙气的小姐姐,俊雅的小哥哥人.
我们知道一个观察员,他可以看到的人,一定是在\(\ge w_i\)时间抵达这个节点.
我们现在考虑刚好在\(w\_i\)时间抵达这个节点的人们,应该满足什么条件?
稍微将这个式子变形一下.
图片表示更加清晰.
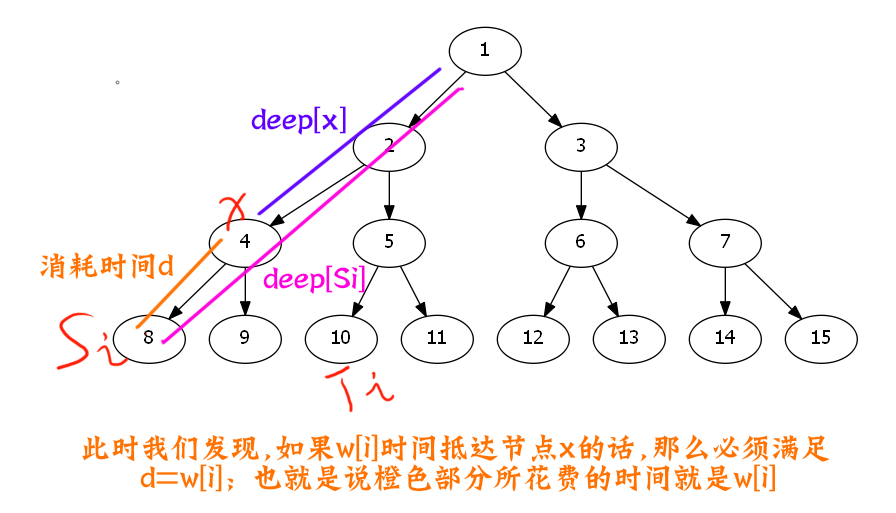
下降链
- 对于红色链而言
橙色链是上升链,而红色链就是下降链.
同理一个点刚好抵达在\(w_i\)的时间,抵达红色链上第i个观察员,所在的位置\(x\),需要满足.
如下图所示
其实就是
特殊统计
我们认真思考一下这道题目的核心统筹方面.
我们知道树上的统计,往往会和树上差分有关,再加上这道题目肯定运用到了Lca算法,所以不难将题目确定为树上差分.
我们需要注意到,只有\(S_i\)到\(Lca(S_i,T_i)\)路径之间的点会产生贡献，如果这个点位于路径之间时，子树和会产生\(+1\)的贡献.
反之在\(S_i\)的子树中,\(T_i\)的子树,\(Lca(S_i,T_i)\)的上方都肯定不会产生贡献.
简而言之,就是对于一个点而言,除非这个点在路径上,否则统统不会被贡献.
不是自己人,一定不会贡献.
上升链
- 对于橙色链而言.
此时的问题,已经变成了.
那么统计数组为.
对于一个物品出现.
那么这个物品所在节点\(x\)的
对于一个物品消失.
那么这个物品所在节点\(x\)的
我们对整棵树进行深度优先遍历.
存储遍历这个节点前,他已经有的物品.
遍历所有的子树节点后,他已经有的物品
然后我们树上差分一下.
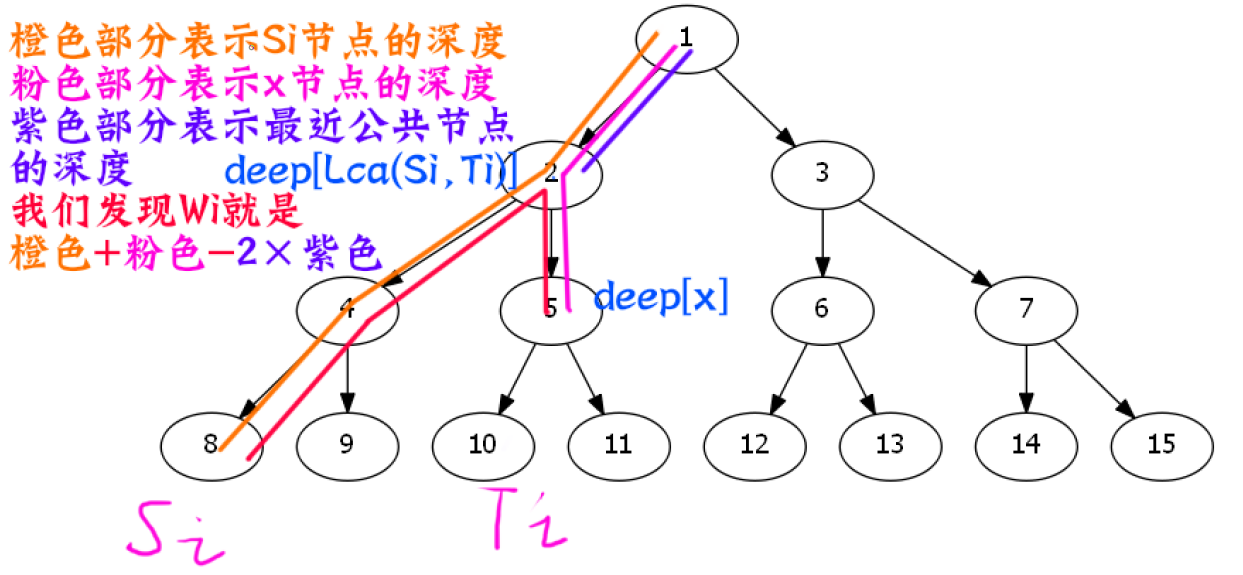
那么这就是我们\(x\)节点处类型为\(W[x]+deep[x]\)的数量.
下降链
- 对于红色链而言
我们需要将物品的类型改一下.
我们还需要将物品产生修改.
同理,物品消失也需要修改.
要记得物品类型可能是负数,需要加上一个偏移量,也就是离散化,成为整数.
比如说
代码解析
#include <bits/stdc++.h>
using namespace std;
const int N=300000+200;
int n,m,w[N],c1[N<<1],c2[N<<1],ans[N<<1];
vector<int> a1[N<<1],b1[N<<1],a2[N<<1],b2[N<<1];
struct LCA
{
int head[N<<1],Next[N<<1],edge[N<<1],ver[N<<1],tot;
int deep[N],fa[N][22],lg[N],date[N];
bool vis[N];
inline void init()
{
memset(head,0,sizeof(head));
memset(deep,0,sizeof(deep));
memset(vis,false,sizeof(vis));
tot=0;
}
inline void add_edge(int a,int b,int c)
{
edge[++tot]=b;
ver[tot]=a;
Next[tot]=head[a];
head[a]=tot;
}
inline void dfs(int x,int y)
{
deep[x]=deep[y]+1;
fa[x][0]=y;
for(int i=1; (1<<i)<=deep[x]; i++)
fa[x][i]=fa[fa[x][i-1]][i-1];
for(int i=head[x]; i; i=Next[i])
if (edge[i]!=y)
dfs(edge[i],x);
return ;
}
inline int Lca(int x,int y)
{
if (deep[x]<deep[y])
swap(x,y);
while(deep[x]>deep[y])
x=fa[x][lg[deep[x]-deep[y]]-1];
if(x==y)
return x;
for(int i=lg[deep[x]]; i>=0; i--)
if (fa[x][i]!=fa[y][i])
{
x=fa[x][i];
y=fa[y][i];
}
return fa[x][0];
}
void query(int x)
{
int val1=c1[deep[x]+w[x]],val2=c2[w[x]-deep[x]+n];
vis[x]=1;
for(int i=head[x]; i; i=Next[i])
{
int y=edge[i];
if (vis[y])
continue;
query(y);
}
for (int i=0; i<a1[x].size(); i++)
c1[a1[x][i]]++;
for (int i=0; i<b1[x].size(); i++)
c1[b1[x][i]]--;
for (int i=0; i<a2[x].size(); i++)
c2[a2[x][i]+n]++;
for (int i=0; i<b2[x].size(); i++)
c2[b2[x][i]+n]--;
ans[x]+=c1[deep[x]+w[x]]-val1+c2[w[x]-deep[x]+n]-val2;
}
} g1;
int main()
{
scanf("%d%d",&n,&m);
g1.init();
for(int i=1; i<n; i++)
{
int a,b;
scanf("%d%d",&a,&b);
g1.add_edge(a,b,0);
g1.add_edge(b,a,0);
}
for(int i=1; i<=n; i++)
scanf("%d",&w[i]);
for(int i=1; i<=n; i++)
g1.lg[i]=g1.lg[i-1]+(1<<g1.lg[i-1]==i);
g1.dfs(1,0);
for(int i=1; i<=m; i++)
{
int a,b;
scanf("%d%d",&a,&b);
int c=g1.Lca(a,b);
a1[a].push_back(g1.deep[a]);
b1[g1.fa[c][0]].push_back(g1.deep[a]);
a2[b].push_back(g1.deep[a]-2*g1.deep[c]);
b2[c].push_back(g1.deep[a]-2*g1.deep[c]);
}
g1.query(1);
for (int i=1; i<=n; i++)
printf("%d ",ans[i]);
return 0;
}
