Trie&可持久化Trie
WARNING:以下代码未经测试,若发现错误,欢迎指出qwq~
Trie树(字典树)
一种简单的数据结构,可存储大量字符串,可在$O(len)$的时间内完成插入,删除,查找等操作。
下面是一个简单的例子,对于abc,abd,abcd,bcd这四个字符串建Trie树,如下图: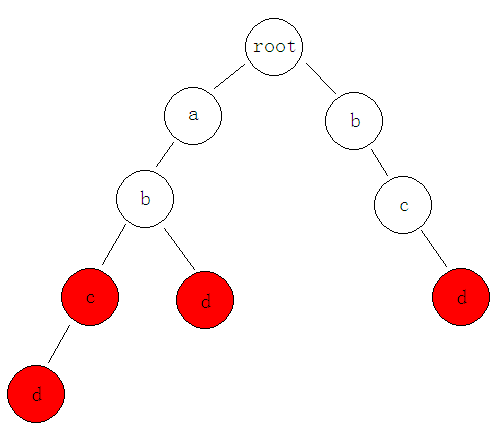
其中,红色节点为一个字符串的结尾。对于任意节点,从根节点到该节点路径上字符组成的字符串即为该节点表示的字符串。
基本操作
相关变量
1 int root,cnt,ch[1000010][26],son[1000010]; 2 bool flag[1000010]; 3 void init(){ 4 memset(flag,false,sizeof(flag)); 5 memset(son,0,sizeof(son)); 6 memset(ch,0,sizeof(ch)); 7 root=cnt=1; 8 return; 9 }
root即为根节点,cnt用于动态建树,ch[i][j]表示i节点的第j个子节点(表示字符char('a'+i))的编号,son[i]表示i节点的子节点数,flag[i]表示i节点是否为某个字符串的末尾。
插入
1 void ins(int rt,int dep){ 2 if(dep==len){ 3 flag[rt]=true; 4 return; 5 } 6 if(!ch[rt][s[dep]-'a']){ 7 ch[rt][s[dep]-'a']=++cnt; 8 son[rt]++; 9 } 10 ins(ch[rt][s[dep]-'a'],dep+1); 11 return; 12 }
删除
1 bool del(int rt,int dep){ 2 if(dep==len){ 3 if(flag[rt]){ 4 flag[rt]=false; 5 return true; 6 } 7 return false; 8 } 9 if(!ch[rt][s[dep]-'a']) 10 return false; 11 if(del(ch[rt][s[dep]-'a'],dep+1)){ 12 if(!son[ch[rt][s[dep]-'a']]&&!flag[ch[rt][s[dep]-'a']]){ 13 ch[rt][s[dep]-'a']=0; 14 son[rt]--; 15 } 16 return true; 17 } 18 return false; 19 }
查找
1 bool query(int rt,int dep){ 2 if(dep==len) 3 return flag[rt]; 4 if(!ch[rt][s[dep]-'a']) 5 return false; 6 return query(ch[rt][s[dep]-'a'],dep+1); 7 }
以上三个是Trie树的基本操作,下面来讲一下Trie树的其它运用。
拓展运用
求第k小字符串
存储以每个节点为根的子树中的末尾节点个数(size[i])即可。
1 void kth(int rt,int dep,int k){ 2 if(k>size[rt]){ 3 puts("have no kth string"); 4 return; 5 } 6 for(int i=0;i<26;i++) 7 if(k>size[ch[rt][i]]) 8 k-=size[ch[rt][i]]; 9 else if(ch[rt][i]){ 10 putchar('a'+i); 11 kth(ch[rt][i],dep+1,k); 12 } 13 return; 14 }
最长公共前缀
用LCA求两个字符串对应的末尾节点的最近公共祖先即可,时间复杂度O(log2n)。
1 代码不贴了,懒~~~
最大异或值
将每个数转化为二进制,添加前缀0至相同位数,然后从最高位开始插入。查询时从最高位开始查询是否有与相应位置异或值为1的节点即可。
1 太水了,也不贴代码了~~~
可持久化Trie树
在做题过程中,我们常常会遇到求区间第k大字符串,区间与某数异或最大值之内的问题,我们便可以采用可持久化Trie树来解决这类问题。
依旧以abc,abd,abcd,bcd这四个字符串为例建可持久化Trie,如下图:
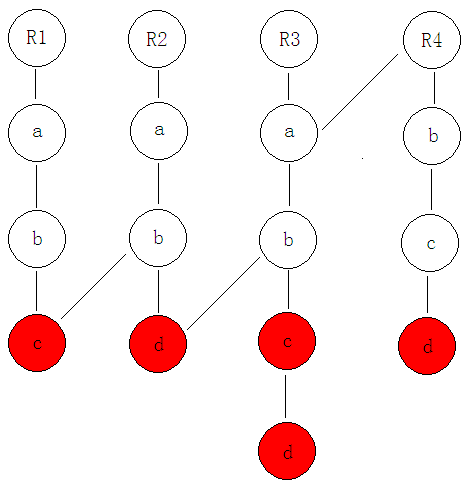
红色节点意义同上。
基本操作
相关变量
1 int cnt=0,root[1000010],size[1000010],ch[1000010][26]; 2 bool flag[1000010]; 3 void init(){ 4 memset(flag,false,sizeof(flag)); 5 memset(root,0,sizeof(root)); 6 memset(size,0,sizeof(size)); 7 memset(ch,0,sizeof(ch)); 8 cnt=0; 9 return; 10 }
意义同上。
插入
1 void ins(int &now,int last,int dep){ 2 if(!now) 3 now=++cnt; 4 if(dep==len){ 5 flag[now]=true; 6 size[now]=size[last]+1; 7 return; 8 } 9 int sign=s[dep]-'a'; 10 for(int i=0;i<26;i++) 11 if(i!=sign){ 12 ch[now][i]=ch[last][i]; 13 size[now]+=size[ch[last][i]]; 14 } 15 ins(ch[now][sign],ch[last][sign],dep+1); 16 size[now]+=size[ch[now][sign]]; 17 return; 18 }
区间第k小查询
1 void kth(int rl,int rr,int dep,int k){ 2 if(k>size[rr]-size[rl]){ 3 puts("have no kth string"); 4 return; 5 } 6 for(int i=0;i<26;i++) 7 if(k>size[ch[rr][i]]-size[ch[rl][i]]) 8 k-=size[ch[rr][i]]-size[ch[rl][i]]; 9 else if(size[ch[rr][i]]-size[ch[rl][i]]>0){ 10 putchar('a'+i); 11 kth(ch[rl][i],ch[rr][i],dep+1,k); 12 return; 13 } 14 return; 15 }
区间最大异或值
1 好吧,还是懒得打~~~


