数据结构笔记(第五章 )
第五章 树
树和森林的概念
自由树:
一棵自由树 Tf 可定义为一个二元组Tf = (V, E) V = {v1, ..., vn} 是由 n (n>0) 个元素组成的有限非空集合,称为顶点集合。 E = {(vi, vj) | vi, vj ∈V, 1≤i, j≤n} 是n-1个序对的集 合,称为边集合,E 中的元素 (vi, vj)称为边或分支。
有根树:
一棵有根树 T,简称为树,它是n (n≥0) 个 结点的有限集合。当n = 0时,T 称为空树;否 则,T 是非空树,记作 T=Ø (n=0) T={r,T1,T2,...,Tm} (n>0).
有根树的特征 :
r 是一个特定的称为根(root)的结点,它只有直 接后继,但没有直接前驱;
根以外的其他结点划分为 m (m 0) 个互不相交 的有限集合T1, T2, …, Tm,每个集合又是一棵树, 并且称之为根的子树。
每棵子树的根结点有且仅有一个直接前驱,但可 以有0个或多个直接后继。
注:树的定义具有递归性,即树中还有树。
树的基本术语:
兄弟 :同一结点的子女互称为兄弟。
分支结点 :度不为0的结点即为分支结点,亦 称为非终端结点。
叶结点 :度为0的结点即为叶结点,亦称为终 端结点。
祖先 :某结点到根结点的路径上的各个结点 都是该结点的祖先。
子孙 :某结点的所有下属结点,都是该结点 的子孙。
结点的层次 :规定根结点在第一层,其子女 结点的层次等于它的层次加一。以下类推。
深度: 结点的深度即为结点的层次;离根最 远结点的层次即为树的深度。
高度 :规定叶结点的高度为1,其双亲结点 的高度等于它的高度加一。
树的高度 :等于根结点的高度,即根结点所 有子女高度的最大值加一。
有序树 :树中结点的各棵子树 T0, T1, …是有 次序的,即为有序树。
无序树 :树中结点的各棵子树之间的次序是 不重要的,可以互相交换位置。
森林 :森林是m(m≥0)棵树的集合。
树的抽象数据类型
template <class T>
class Tree {
//对象: 树是由n (≥0) 个结点组成的有限集合。
//在类界面中的 position 是树中结点的地址。
//在顺序存储方式下是下标型, 在链表存储方式下是指针型。
//T 是树结点中存放数据的类型, 要求所有结点的数据类型都是一致的。
public:
Tree ();
~Tree ();
BuildRoot (const T& value); //建立树的根结点
position FirstChild(position p); //返回 p 第一个子女地址, 无子女返回 0
position NextSibling(position p); //返回 p 下一兄弟地址, 若无下一兄弟返回 0
position Parent(position p); //返回 p 双亲结点地址, 若 p 为根返回 0
getData(position p); //返回结点 p 中存放的值
bool InsertChild(position p, T& value);//在结点p下插入值为 value 的新子女, 若插
//入失败, 函数返回false, 否则返回true
bool DeleteChild (position p, int i); //删除结点 p 的第 i 个子女及其全部子孙结
//点, 若删除失败, 则返回false, 否则返回true
void DeleteSubTree (position t); //删除以 t 为根结点的子树
bool IsEmpty (); //判树空否, 若空则返回true, 否则返回false
void Traversal (void (*visit)(position p)); //遍历以 p 为根的子树 };
二叉树
为何要重点研究每结点最多只有两个 “叉” 的树?
二叉树的结构最简单,规律性最强;
可以证明,所有树都能转为唯一对应的二叉树,不失一般性。
二叉树的定义
一棵二叉树是结点的一个有限集合,该集合 或者为空,或者是由一个根结点加上两 棵分别称为左子树和右子树的、互不相交的 二叉树组成。 (5种形态)
逻辑结构:
一对二(1:2)
基本特征:
① 每个结点最多只有两棵子树(不存在度大于2的结 点);
② 左子树和右子树次序不能颠倒(有序树
特殊二叉树的定义
定义1 满二叉树 (Full Binary Tree) :
每一层结点都达 到了最大个数的二叉树。深度为k的满二叉树有2^k - 1个。
定义2 完全二叉树 (Complete Binary Tree) :
若设二叉树的深度为 k,则共有 k 层。除第 k 层外, 其它各层 (1—k-1) 的结点数都达到最大个数,第k层 从右向左连续缺若干结点,这就是完全二叉树。
满二叉树和完全二叉树有什么区别?
满二叉树是叶子一个也不少的树,而完全二叉树虽然前n-1层是满的,但最底层却允许在右边缺少连续若干个结点。满二叉树是完全二叉树的一个特例。
二叉树的抽象数据类型
基本操作:
第一类, 查询 :寻找满足某种特定关系的结点;查询树的属性: 如高度深度,节点个数,状态, 特定节点,极其父子节点。
第二类, 插入、修改或删除:如在树的当前结点上插入一个新 结点或删除当前结点的孩子结点等。
第三类, 上述操作必须建立在对树结点能够“遍历”的基础上, 遍历树中每个结点,这里着重介绍。
遍历:指每个结点都被访问且仅访问一次,不遗漏不重复
template <class T>
class BinaryTree { //对象: 结点的有限集合, 二叉树是有序树
public:
BinaryTree (); //构造函数
BinaryTree (BinTreeNode<T> *lch,
BinTreeNode<T> *rch, T item); //构造函数, 以item为根, lch和rch为左、右子树构造一棵二叉树
int Height (); //求树高度
int Size (); //求树中结点个数
bool IsEmpty (); //判二叉树空否?
BinTreeNode<T> *Parent (BinTreeNode<T> *t); //求结点 t 的双亲
BinTreeNode<T> *LeftChild (BinTreeNode<T> *t); //求结点 t 的左子女
BinTreeNode<T> *RightChild (BinTreeNode<T> *t); //求结点 t 的右子女
bool Find (T& item); //判断item是否在树中
bool getData (T& item); //取得结点数据
bool Insert (T item); //在树中插入新元素
bool Remove (T item); //在树中删除元素
BinTreeNode<T> *getRoot (); //取根
void preOrder (void (*visit) (BinTreeNode<T> *t)); //前序遍历, visit是访问函数 void
inOrder (void (*visit) (BinTreeNode<T> *t)); //中序遍历, visit是访问函数 void
postOrder (void (*visit) (BinTreeNode<T> *t)); //后序遍历, (*visit)是访问函数 void
levelOrder (void (*visit)(BinTreeNode<T> *t)); //层次序遍历, visit是访问函数
};
二叉树的性质
性质1 若二叉树结点的层次从 1 开始, 则在 二叉树的第 i 层最多有 2^(i-1) 个结点。( i≥1)
性质2 深度为 k 的二叉树最少有 k 个结点, 最多有 2^k - 1个结点。( k≥1 ) 因为每一层最少要有1个结点,因此,最少 结点数为 k。最多结点个数借助性质1:用 求等比级数前k项和的公式。
性质3 对任何一棵二叉树,如果其叶结点有 n0 个, 度为 2 的非叶结点有 n2 个, 则有n0=n2+1
性质4 具有 n (n≥0) 个结点的完全二叉树的深 度为 log(2) (n+1)
性质5 如将一棵有n个结点的完全二叉树自顶向 下,同一层自左向右连续给结点编号1, 2, …, n, 则有以下关系: 若i = 1, 则 i 无双亲
若i > 1, 则 i 的双亲为[i/2]
i 的左子女为 2 * i( 如果 i 有左子女的话 ), i 的右子女为2*i+1 ( 如果 i 有右子女的话 )
若 i 为奇数, 且i != 1, 则其左兄弟为i-1,
若 i 为偶数, 且i != n, 则其右兄弟为i+1
若二叉树用二叉链表作存贮结构,则在n个结点的二 叉树链表中只有n-1个非空指针域
具有n个结点的完全二叉树有[(n-1)/2]或(n-1/2 n/2-1个度为2的结点
二叉树的顺序表示
顺序存储结构:用一组地址连续的存储单元存储二 叉树中的数据元素。
//二叉树的顺序存储结构的定义如下:
const MAXSIZE = 100; // 暂定二叉树中结点数的最大值为100
typedef struct {
ElemType *data; // 存储空间基址 //(初始化时分配空间)
int nodeNum; // 二叉树中结点数
} SqBiTree; // 二叉树的顺序存储结构
按二叉树的结点“自上而下、 从左至右”编号,用一组连 续的存储单元存储。
问:顺序存储后能否复原成唯一对应的二叉树形状?
答:若是完全/满二叉树则可以做到唯一复原。 因为根据性质5:可知结点i,左孩子的下标值必为2i, 其右孩子的下标值必为2i+1. 非完全二叉树要将各层空缺处统统补上“虚结点”,其内容为空。
缺点:①浪费空间;②插入、删除不便 结论:非完全二叉树不适合进行顺序存储
二叉树的链表表示(二叉链表)
二叉树结点定义:每个结点有3个数据成员, data域存储结点数据,leftChild和rightChild分 别存放指向左子女和右子女的指针。
//二叉树的二叉链表存储简单可以表示
class BiTNode {
ElemType data;
struct BiTNode *Lchild, *Rchild; // 左、右孩子指针
} *BiTree;
一般从根结点开始存储。(相应地,访问树中结点时 也只能从根开始)
含n个结点的二叉链表其中空链域为n+1个
二叉树的链表表示(三叉链表)
每个结点增加一个指向双亲的指针parent, 使得查找双亲也很方便。
//二叉树c++的类定义
template <class T>
struct BinTreeNode { //二叉树结点类定义
T data; //数据域
BinTreeNode<T> *leftChild, *rightChild; //左子女、右子女链域
BinTreeNode () //构造函数
{ leftChild = NULL; rightChild = NULL; }
BinTreeNode (T& x, BinTreeNode<T> *l = NULL,BinTreeNode<T> *r = NULL)
{ data = x; leftChild = l; rightChild = r; }
};
template <class T>
class BinaryTree { //二叉树类定义
protected:
BinTreeNode<T> *root; //二叉树的根指针
T RefValue; //数据输入停止标志
public:
BinaryTree () : root (NULL) { } //构造函数
BinaryTree (T value) : RefValue(value), root(NULL) { }
BinaryTree (BinaryTree<T>& s); //复制构造函数
~BinaryTree () { destroy(root); } //析构函数
bool IsEmpty () { return root == NULL;}//判二叉树空否
int Height () { return Height(root); } //求树高度
BinTreeNode<T> *Parent (BinTreeNode <T> *t)
{ return (root == NULL || root == t) ?NULL : Parent (root, t); } //返回双亲结点
BinTreeNode<T> *LeftChild (BinTreeNode<T> *t)
{ return (t != NULL)?t->leftChild : NULL; }
//返回左子女
BinTreeNode<T> *RightChild (BinTreeNode<T> *t)
{ return (t != NULL)?t->rightChild : NULL; }
//返回右子女
BinTreeNode<T> *getRoot () const { return root; } //取根
void preOrder (void (*visit) (BinTreeNode<T> *t))
{ preOrder (root, visit); } //前序遍历
void inOrder (void (*visit) (BinTreeNode<T> *t))
{ inOrder (root, visit); } //中序遍历
void postOrder (void (*visit) (BinTreeNode<T> *t))
{ postOrder (root, visit); } //后序遍历
void levelOrder (void (*visit)(BinTreeNode<T> *t));
//层次序遍历
int Insert (const T item); //插入新元素
BinTreeNode<T> *Find (T item) const; //搜索
protected:
void CreateBinTree (istream& in,BinTreeNode<T> *& subTree);
//从文件读入建树
bool Insert (BinTreeNode<T> *& subTree, T& x);
//插入
void destroy (BinTreeNode<T> *& subTree); //删除
bool Find (BinTreeNode<T> *subTree, T& x); // 查找
BinTreeNode<T> *Copy (BinTreeNode<T> *r); //复制
int Height (BinTreeNode<T> *subTree); //返回树高度
int Size (BinTreeNode<T> *subTree); //返回结点数
BinTreeNode<T> *Parent (BinTreeNode<T> *subTree, BinTreeNode<T> *t); //返回父结点
BinTreeNode<T> *Find (BinTreeNode<T> *subTree, T& x) const; //搜寻x
void Traverse (BinTreeNode<T> *subTree, ostream& out); //前序遍历输出
void preOrder (BinTreeNode<T>& subTree,void (*visit) (BinTreeNode<T> *t)); //前序遍历
void inOrder (BinTreeNode<T>& subTree,void (*visit) (BinTreeNode<T> *t)); //中序遍历
void postOrder (BinTreeNode<T>& subTree,void (*visit) (BinTreeNode<T> *t));//后序遍历
friend istream& operator >> (istream& in,BinaryTree<T>& Tree); //重载操作:输入
friend ostream& operator << (ostream& out,BinaryTree<T>& Tree); //重载操作:输出
};
二叉树遍历
遍历——指按某条搜索路线遍访每个结点,使得 每个结点均被访问一次,而且仅被访问一次(又 称周游)。
遍历用途——它是树结构插入、删除、修改、查 找和排序运算的前提,是二叉树一切运算的基础 和核心。
遍历方法——牢记一种约定,对每个结点的查看 都是“先左后右” 。
“遍历”是任何类型均有的操作,对线性结构而言,只有一条搜索路径(因为每个结点均只 有一个后继),故不需要另加讨论。 而二叉树是非线性结构,每个结点有两个后继, 则存在如何遍历即按什么样的搜索路径遍历的问题
二叉树的遍历就是按某种次序访问树中的结点,要求每个结点访问一次且仅访问一次。遍历可认为是 将一棵树进行线性化的处理。 对“二叉树”而言,可以有两类搜索策略: 1. 先上后下的按层次遍历。 2. 先左(子树)后(子树)的深度遍历。
若限定子树先左后右访问,则对根的访问时机不同 ,有三种实现方案:
DLR 先 (根)序遍历
LDR 中 (根)序遍历
LRD 后(根)序遍历
注:“先、中、后”的意思是指访问的结点D是先于子树出现还是后于子树出现。
先序遍历二叉树
若二叉树为空,则 空操作;否则 (1) 访问根结点; (2) 先序遍历左子树; (3) 先序遍历右子树。
中序遍历二叉树
若二叉树为空, 则空操作;否则 (1) 中序遍历 左子树; (2) 访问根结点; (3) 中序遍历右子树。
后序遍历二叉树
若二叉树为空,则 空操作;否则 (1) 后序遍历 左子树; (2) 后序遍历 右子树; (3) 访问根结点
//二叉树C++版递归中序遍历算法
template <class T>
void BinaryTree<T>::InOrder (BinTreeNode<T> * subTree, void (*visit) (BinTreeNode<T> *t))
{
if (subTree != NULL) {
InOrder (subTree->leftChild, visit);
//遍历左子树
visit (subTree); //访问根结点
InOrder (subTree->rightChild, visit); //遍历右子树 }
};
void inOrder (void (*visit) (BinTreeNode<T> *t))
{ inOrder (root, visit); } //中序遍历
//二叉树递归的c++版前序遍历算法
template <class T> void BinaryTree<T>::PreOrder (BinTreeNode<T> * subTree, void (*visit) (BinTreeNode<T> *t))
{
if (subTree != NULL)
{
visit (subTree); //访问根结点
PreOrder (subTree->leftChild, visit); //遍历左子树
PreOrder (subTree->rightChild, visit); //遍历右子树
}
};
void PreOrder (void (*visit) (BinTreeNode<T> *t))
{ PreOrder (root, visit); } //先序遍历
//二叉树递归的c++版后序遍历算法
template <class T>
void BinaryTree<T>::PostOrder (BinTreeNode<T> * subTree, void (*visit) (BinTreeNode<T> *t ) ){
if (subTree != NULL ) {
PostOrder (subTree->leftChild, visit); //遍历左子树
PostOrder (subTree->rightChild, visit); //遍历右子树
visit (subTree); //访问根结点
}
};
下面我们再给出两个遍历二叉树的技巧:
(1)对一棵二叉树中序遍历时,若我们将二叉树严格地按左 子树的所有结点位于根结点的左侧,右子树的所有结点 位于根右侧的形式绘制,就可以对每个结点做一条垂线,映射到下面的水平线上,由此得到的顺序就是该二 叉树的中序遍历序列。
(2)任何一棵二叉树都可以将它的外部轮廓用 一条线绘制出来,我们将它称为二叉树的包线 ,这条包线对于理解二叉树的遍历过程很有用
从虚线的出发点到终点的路径 上,每个结点经过3次。
第1次经过时访问=先序遍历
第2次经过时访问=中序遍历
第3次经过时访问=后序遍历
由此可以看出:
(1)遍历操作实际上是将非线性结构线性化的过 程,其结果为线性序列,并根据采用的遍历顺 序分别称为先序序列、中序序列或后序序列;
(2)深度遍历操作是一个递归的过程,因此, 这三种遍历操作的算法用递归函数实现最简单 。
利用二叉树前序遍历建立二叉树,以递归方式建立二叉树。
输入结点值的顺序必须对应二叉树结点前序 遍历的顺序。并约定以输入序列中不可能出 现的值作为空结点的值以结束递归, 此值在 RefValue中。例如用“#”或用“-1”表示字 符序列或正整数序列空结点。
template <class T>
void BiTree<T>::Creat(BiNode<T> * &bt) {
cin >> ch; //输入结点的数据信息,假设为字符
if (ch == '# ') bt = NULL; //建立一棵空树
else {
bt = new BiNode(ch); //生成一个结点,数据域为ch
if (bt == NULL) {cerr << “存储分配错!” << endl; exit (1);}
Creat(bt->lchild); //递归建立左子树
Creat(bt->rchild); //递归建立右子树 }}
binNode* BinTree::create()
{
char temp ;
binNode* T; //读入字符 ,如是空格,结束否则生成节点,左,右子树
cin>>temp ;
if (temp=='@') return NULL ;
else{
T =new binNode(temp) ;
T->lchild=create( );
T->rchild=create();
return T; }
}
BinTree::BinTree(void) { root=create(); }
template<class T>
void BinaryTree<T>::CreateBinTree (istream& in, BinTreeNode<T> *& subTree)
{ //私有函数: 以递归方式建立二叉树。
T item;
if ( !in.eof () )
{ //未读完, 读入并建树
in >> item; //读入根结点的值
if (item != RefValue) {
subTree = new BinTreeNode<T>(item); //建立根结点
if (subTree == NULL)
{cerr << “存储分配错!” << endl; exit (1);}
CreateBinTree (in, subTree->leftChild); CreateBinTree (in, subTree->rightChild);
}
else subTree = NULL; //封闭指向空子树的指针
}
};
template<class T>
istream& operator >> (istream& in, BinaryTree<T>& Tree)
{ //重载操作: 输入并建立一棵二叉树Tree。in是输入流对象。
CreateBinTree (in, Tree.root); //建立二叉树
return in; };
template <class T>
BinTreeNode<T> *BinaryTree<T>:: Parent (BinTreeNode <T> *subTree, BinTreeNode <T> *t) {
//从结点 subTree 开始, 搜索结点 t 的双亲, 若找
//到则返回双亲结点地址, 否则返回NULL
if (subTree == NULL) return NULL;
if (subTree->leftChild == t || subTree->rightChild == t)
return subTree; //找到, 返回父结点地址
BinTreeNode <T> *p;
if ((p = Parent (subTree->leftChild, t)) != NULL)
return p; //递归在左子树中搜索
else return Parent (subTree->rightChild, t); //递归在左子树中搜索 };
BinTreeNode<T> *Parent (BinTreeNode <T> *t)
{ return (root == NULL || root == t) ? NULL : Parent (root, t); } //返回双亲结点
template<class T>
void BinaryTree<T>::destroy (BinTreeNode<T> * subTree) {
//私有函数: 删除根为subTree的子树
if (subTree != NULL) {
destroy (subTree->leftChild); //删除左子树
destroy (subTree->rightChild); //删除右子树
delete subTree; //删除根结点
}
};
~BinaryTree () { destroy(root); } //析构函数
二叉树遍历的非递归算法
前序遍历——非递归算法(伪代码)
1.栈s初始化;
2.循环直到p为空且栈s为空
2.1 当p不空时循环
2.1.1 输出p->data;
2.1.2 将指针p的值保存到栈中;
2.1.3 继续遍历p的左子树
2.2 如果栈s不空,则
2.2.1 将栈顶元素弹出至p;
2.2.2 准备遍历p的右子树;
template <class T>
void BinaryTree<T>::preOrder (void (*visit) (BinTreeNode<T> *t))
{
stack<BinTreeNode<T>*> S;
BinTreeNode<T> *p = root;
do { while (p != NULL) { //遍历指针向左下移动
visit(p);
S.Push (p); //该子树沿途结点进栈
p = p->leftChild; }
if (!S.IsEmpty()) { //栈不空时退栈
S.Pop (p); //退栈
p = p->rightChild; //遍历指针进到右子女 }
} while (p != NULL || !S.IsEmpty ());
}
中序遍历——非递归算法
在二叉树的中序遍历中,访问结点的操作发生在 该结点的左子树遍历完毕并准备遍历右子树时, •所以,在遍历过程中遇到某结点时并不能立即访 问它,而是将它压栈,等到它的左子树遍历完毕后, 再从栈中弹出并访问之。
中序遍历的非递归算法只需将前序遍历的非递归 算法中的访问语句,移到S.Pop (p)出栈之后即可。
template <class T>
void BinaryTree<T>::InOrder (void (*visit) (BinTreeNode<T> *t))
{ stack<BinTreeNode<T>*> S;
BinTreeNode<T> *p = root;
do { while (p != NULL) { //遍历指针向左下移动
S.Push (p); //该子树沿途结点进栈
p = p->leftChild; }
if (!S.IsEmpty()) { //栈不空时退栈
S.Pop (p);
visit (p); //退栈, 访问
p = p->rightChild; //遍历指针进到右子女 }
} while (p != NULL || !S.IsEmpty ());
}
后序遍历的非递归算法
//后序遍历的非递归算法
template <class T>
void BinaryTree<T>:: PostOrder (void (*visit) (BinTreeNode<T> *t)
{
Stack<stkNode<T>> S;
stkNode<T> w;
BinTreeNode<T> * p = root; //p是遍历指针
do {
while (p != NULL) {
w.ptr = p;
w.tag = L;
S.Push (w);
p = p->leftChild; }
int continue1 = 1; //继续循环标记, 用于R
while (continue1 && !S.IsEmpty ()) {
S.Pop (w); p = w.ptr;
switch (w.tag) { //判断栈顶的tag标记
case L: w.tag = R; S.Push (w);
continue1 = 0;
p = p->rightChild; break;
case R: visit (p); break;
}
}
} while (!S.IsEmpty ()); //继续遍历其他结点
cout << endl;
};
层次序遍历的算法
template <class T>
void BinaryTree<T>:: levelOrder (void (*visit) (BinTreeNode<T> *t)) {
if (root == NULL) return;
Queue<BinTreeNode<T> * > Q;
BinTreeNode<T> *p = root;
Q.EnQueue (p);
while (!Q.IsEmpty ()) {
Q.DeQueue (p);
visit(p);
if (p->leftChild != NULL) Q.EnQueue (p->leftChild);
if (p->rightChild != NULL) Q.EnQueue (p->rightChild); } };
template <class T>//判断是否完全二叉树,是则返回1,否则返回0
int levelOrder (BitTreeNode<T> * root) {
if (root == NULL) return 0;
Queue<BinTreeNode<T> *> Q;
BinTreeNode<T> *p = root;
Q.EnQueue (p);
while (!Q.IsEmpty ()) {
Q.DeQueue (p);
if(!p) flag=1;
else if(flag)return 0;
else { Q.EnQueue (p->leftChild);
Q.EnQueue (p->rightChild); } }
return 1; }
二叉树的计数
//设计算法按前序次序打印二叉树中的叶子结点。
void PreOrder(BiNode *root) {
if (root == NULL) return;
else {
if (root->lchild ==NULL && root->rchild==NULL)
cout<<root->data;
PreOrder(root->lchild);
PreOrder(root->rchild); }
}
//设计算法求二叉树中的叶子结点个数。
int CountLeaf (BiNode * T) {// 先序遍历二叉树,以 count 返回二叉树中叶子结点数
if ( T ==null) return 0;
else if ((!T->Lchild)&& (!T->Rchild))
return 1; // 对叶子结点计数
else{
int a=CountLeaf( T->Lchild) ;
int b = CountLeaf( T->Rchild);
return a+b;
}
}
} // CountLeaf
void CountLeaf (BiNode * T, int& count) {// 先序遍历二叉树,以 count 返回二叉树中叶子结点数
if ( T ) {
if ((!T->Lchild)&& (!T->Rchild)) count++; // 对叶子结点计数
else{
CountLeaf( T->Lchild, count);
CountLeaf( T->Rchild, count);
}
} // if
} // CountLeaf
由先序序列确定根结点 再由中序序列找出左右子树。 可唯一确定一棵二叉树!
已知后序序列和中序序列也可以唯一确定一棵二叉树 。
树与森林
树的存储表示
1、广义表表示
2、父指针表示
树中结点的存放顺序一般不做特殊要求,但 为了操作实现的方便,有时也会规定结点的 存放顺序。
此存储结构找父节点的时间复杂度为O(1),但 找子女需遍历整个数组。
3、子女链表表示
无序树情形链表中各结点顺序任意,有序树 必须自左向右链接各个子女结点。
4、子女-兄弟表示
也称为树的二叉树表示。
firstChild 指向该结点的第一个子女结点。无 序树时,可任意指定一个结点为第一个子女。
nextSibling 指向该结点的下一个兄弟。任一 结点在存储时总是有顺序的。
若想找某结点的所有子女,可先找firstChild, 再反复用 nextSibling 沿链扫描。
//用子女-兄弟表示的 树的类定义
template <class T> struct TreeNode { //树的结点类
T data; //结点数据
TreeNode<T> *firstChild, *nextSibling; //子女及兄弟指针
TreeNode (T value = 0, TreeNode<T> *fc = NULLTreeNode<T> *ns = NULL) //构造函数 : data (value), firstChild (fc), nextSibling (ns) { } };
template <class T>
class Tree { //树类
private:
TreeNode<T> *root, *current; //根指针及当前指针
int Find (TreeNode<T> *p, T value); //在以p为根的树中搜索value
void RemovesubTree (TreeNode<T> *p); //删除以p为根的子树
bool FindParent (TreeNode<T> *t, TreeNode<T> *p);
public:
Tree () { root = current = NULL; } //构造函数
bool Root (); //置根结点为当前结点
bool IsEmpty () { return root == NULL; }
bool FirstChild (); //将当前结点的第一个子女置为当前结点
bool NextSibling (); //将当前结点的下一个兄弟置为当前结点
bool Parent (); //将当前结点的双亲置为当前结点
bool Find (T value); //搜索含value的结点, 使之成为当前结点
…… //树的其他公共操作
};
//子女-兄弟链表常用操作的实现
template <class T> bool Tree<T>::Parent () { //置当前结点的双亲结点为当前结点 TreeNode<T> *p = current;
if (current == NULL || current == root)
{ current = NULL;
return false;
} //空树或根无双亲
return FindParent (root, p); //从根开始找*p的双亲结点
};
template <class T>
bool Tree<T>:: FindParent (TreeNode<T> *t, TreeNode<T> *p) { //在根为*t的树中找*p的双亲, 并置为当前结点
TreeNode<T> *q = t->firstChild; //*q是*t长子
bool succ;
while (q != NULL && q != p) { //扫描兄弟链
if ((succ = FindParent (q, p)) == true)
return succ; //递归搜索以*q为根的子树
q = q->nextSibling; }
if (q != NULL && q == p) {
current = t; return true; }
else { current = NULL; return false; } //未找到 };
template <class T>
bool Tree<T>::FirstChild () { //在树中找当前结点的长子, 并置为当前结点
if (current && current->firstChild )
{ current = current->firstChild; return true; }
current = NULL;
return false;
};
template <class T>
bool Tree<T>::NextSibling () { //在树中找当前结点的兄弟, 并置为当前结点
if (current && current->nextSibling) {
current = current->nextSibling;
return true; }
current = NULL;
return false;
};
树、森林与二叉树的转换
树:兄弟关系 二叉树:双亲和右孩子
树:双亲和长子 二叉树:双亲和左孩子
树转换为二叉树
⑴加线——树中所有相邻兄弟之间加一条连线。
⑵去线——对树中的每个结点,只保留它与第一个 孩子结点之间的连线,删去它与其它孩子结点之间 的连线。
⑶层次调整——以根结点为轴心,将树顺时针转动 一定的角度,使之层次分明。
将一般树化为二叉树表示就是用树的子女-兄 弟表示来存储树的结构。
森林与二叉树表示的转换可以借助树的二叉树 表示来实现。
森林转换为二叉树
⑴ 将森林中的每棵树转换成二叉树;
⑵ 从第二棵二叉树开始,依次把后一棵二叉树的根 结点作为前一棵二叉树根结点的右孩子,当所有二 叉树连起来后,此时所得到的二叉树就是由森林转 换得到的二叉树。
二叉树转换为树或森林
⑴ 加线——若某结点x是其双亲y的左孩子,则把结点x 的右孩子、右孩子的右孩子、……,都与结点y用线连 起来
⑵ 去线——删去原二叉树中所有的双亲结点与右孩子结 点的连线
⑶ 层次调整——整理由⑴、⑵两步所得到的树或森林, 使之层次分明。
//树的先根次序遍历的递归算法
template <class T> void Tree<T>:: PreOrder ( void (*visit) (BinTreeNode<T> *t) ) { //以当前指针current为根, 先根次序遍历
if (!IsEmpty ()) { //树非空
visit (current); //访问根结点
TreeNode<T> *p = current; //暂存当前指针
current = current->firstChild; //第一棵子树
while (current != NULL) {
PreOrder (visit); //递归先根遍历子树
current = current->nextSibling; }
current = p; //恢复当前指针 }
}
//树的后根次序遍历的递归算法
template <class T> void Tree<T> :: PostOrder (void (*visit) (BinTreeNode<T> *t)) { //以当前指针current为根, 按后根次序遍历树
if ( ! IsEmpty () ) { //树非空
TreeNode<T> *p = current; //保存当前指针
current = current->firstChild; //第一棵子树
while (current != NULL) { //逐棵子树
PostOrder (visit);
current = current->nextSibling; }
current = p; //恢复当前指针
visit (current); //访问根结点 }
};
//广度优先(层次次序)遍历
template <class T> void Tree<T>:: LevelOrder(void (*visit) (BinTreeNode<T> *t) ) {
//按广度优先次序分层遍历树, 树的根结点是 //当前指针current。
Queue<TreeNode<T>*> Q; TreeNode<T> *p; if (current != NULL) { //树不空
p = current; //保存当前指针
Q.EnQueue (current); //根结点进队列 }
while (!Q.IsEmpty ()) {
Q.DeQueue (current); //退出队列
visit (current); //访问之
current = current->firstChild;
while (current != NULL) {
Q.EnQueue (current);
current = current->nextSibling; }
current = p; //恢复算法开始的当前指针 }
};
森林的遍历
森林的遍历也分为深度优先遍历和广度优先 遍历,深度优先遍历又可分为先根次序遍历 和后根次序遍历。
森林的先根次序遍历的结果序列 相当于对应二叉树的前序遍历结果。
森林的后根次序遍历的结果序列 相当于对应二叉树中序遍历的结果。
Huffman树
带权路径长度 (Weighted Path Length, WPL)
在很多应用问题中为树的叶结点赋予一个权值,用于表示出现频度、概率值等。因此,在问题处理中把叶结点定义得不同于非叶结点,把叶结点看成“外结点”,非叶结点看成“内结点”。这样的二叉树称为扩充二叉树。
扩充二叉树中只有度为 2 的内结点和度为 0的外结点。根据二叉树的性质,有 n 个外结点就有 n-1 个内结点,总结点数为2n-1。
若一棵扩充二叉树有 n 个外结点,第 i 个外结点的权值为wi,它到根的路径长度为li,则该外结点到根的带权路径长度为wi*li。
扩充二叉树的带权路径长度定义为树的各外结点到根的带权路径长度之和。
WPL=wi*li(求和,i从1到n)
对于同样一组权值,如果放在外结点上,组织方式不同,带权路径长度也不同。
带权路径长度达到最小的扩充二叉树即为Huffman树。
在Huffman树中,权值大的结点离根最近。
Huffman树的构造算法
1.由给定 n 个权值 {w0, w1, w2, …, wn-1},构造 具有 n 棵扩充二叉树的森林 F = { T0, T1, T2,
…, Tn-1 },其中每棵扩充二叉树 Ti 只有一个带权值 wi 的根结点, 其左、右子树均为空。
2.重复以下步骤, 直到 F 中仅剩一棵树为止:
在 F 中选取两棵根结点的权值最小的扩充二叉树, 做为左、右子树构造一棵新的二叉树。置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
在 F 中删去这两棵二叉树。
把新的二叉树加入 F。
//Huffman树的类定义
#include "heap.h"
const int DefaultSize = 20; //缺省权值集合大小
template <class T, class E>
struct HuffmanNode { //树结点的类定义
E data; //结点数据
HuffmanNode<T, E> *parent;
HuffmanNode<T, E> *leftChild, *rightChild;
//左、右子女和父结点指针
HuffmanNode () : Parent(NULL), leftChild(NULL),
rightChild(NULL) { } //构造函数
HuffmanNode (E elem, //构造函数
HuffmanNode<T, E> *pr = NULL,
HuffmanNode<T, E> *left = NULL,
HuffmanNode<T, E> *right = NULL)
: data (elem), parent (pr), leftChild (left),
rightChild (right) { }
};
template <class T, class E>
class HuffmanTree { //Huffman树类定义
public:
HuffmanTree (E w[], int n); //构造函数
~HuffmanTree() { delete Tree(root);} //析构函数
protected:
HuffmanNode<T, E> *root; //树的根
void deleteTree (HuffmanNode<T, E> *t); //删除以 t 为根的子树
void mergeTree (HuffmanNode<T, E>& ht1, HuffmanNode<T, E>& ht2,
HuffmanNode<T, E> *& parent);
};
//建立Huffman树的算法
template <class T, class E>
HuffmanTree<T, E>::HuffmanTree (E w[], int n) {
//给出 n 个权值w[1]~w[n], 构造Huffman树
minHeap<T, E> hp; //使用最小堆存放森林
HuffmanNode<T, E> *parent, &first, &second;
HuffmanNode<T, E> *NodeList =
new HuffmanNode<T,E>[n]; //森林
for (int i = 0; i < n; i++) {
NodeList[i].data = w[i+1];
NodeList[i].leftChild = NULL;
NodeList[i].rightChild = NULL;
NodeList[i].parent = NULL;
hp.Insert(NodeList[i]); //插入最小堆中
}
for (i = 0; i < n-1; i++) { //n-1趟, 建Huffman树
hp.Remove (first); //根权值最小的树
hp.Remove (second); //根权值次小的树
merge (first, second, parent); //合并
hp.Insert (*parent); //重新插入堆中
root = parent; //建立根结点
}
};
template <class T, class E>
void HuffmanTree<T, E>::
mergeTree (HuffmanNode<T, E>& bt1,
HuffmanNode<T, E>& bt2,
HuffmanNode<T, E> *& parent) {
parent = new E;
parent->leftChild = &bt1;
parent->rightChild = &bt2;
parent->data.key =
bt1.root->data.key+bt2.root->data.key;
bt1.root->parent = bt2.root->parent = parent;
};
//采用静态链表的Huffman树
const int n = 20;
const int m = 2*n-1;
typedef struct {
float weight;
int parent, lchild, rchild;
} HTNode;
typedef HTNode HuffmanTree[m];
//建立Huffman树的算法
void CreateHuffmanTree (HuffmanTree T,
float fr[ ], int n) {
for (int i = 0; i < n; i++) T[i].weight = fr[i];
for (i = 0; i < m; i++) {
T[i].parent = T[i].lchild = T[i].rchild = -1;
}
for (i = n; i < m; i++) { //求n-1次根
int min1 = min2 = MaxNum;
int pos1, pos2;
for (int j = 0; j < i; j++) //检测前 i 棵树
if (T[j].parent == -1) //可参选的树根
if (T[j].weight < min1) { //选最小
pos2 = pos1; min2 = min1;
pos1 = j; min1 = T[j].weight;
}
else if (T[j].weight < min2) //选次小
{ pos2 = j; min2 = T[j].weight; }
T[i].lchild = pos1; T[i].rchild = pos2;
T[i].weight = T[pos1].weight+T[pos2].weight;
T[pos1].parent = T[pos2].parent = i;
}
};
最佳判定树
利用Huffman树,可以在构造判定树(决策树)时让平均判定(比较)次数达到最小。
判定树是一棵扩展二叉树,外结点是比较结果,内结点是比较过程,外结点所带权值是概率。
Huffman编码
主要用途是实现数据压缩。设给出一段报文:
CAST CAST SAT AT A TASA
字符集合是 { C, A, S, T },各个字符出现的频度(次数)是 W={ 2, 7, 4, 5 }。
若给每个字符以等长编码(2位二进制足够)
A : 00 T : 10 C : 01 S : 11
则总编码长度为 ( 2+7+4+5 ) * 2 = 36。
若按各个字符出现的概率不同而给予不等长编码,可望减少总编码长度。
各字符出现概率为{ 2/18, 7/18, 4/18, 5/18 },化整为 { 2, 7, 4, 5 }。以它们为各叶结点上的权值, 建立Huffman树。左分支赋 0,右分支赋 1,得Huffman编码(变长编码)。
A : 0 T : 10 C : 110 S : 111
它的总编码长度:71+52+( 2+4 )*3 = 35。比等长编码的情形要短。
总编码长度正好等于Huffman树的带权路径长度WPL。
Huffman编码是一种前缀编码,即任一个二进制编码不是其他二进制编码的前缀。解码时不会混淆。
堆
堆的定义
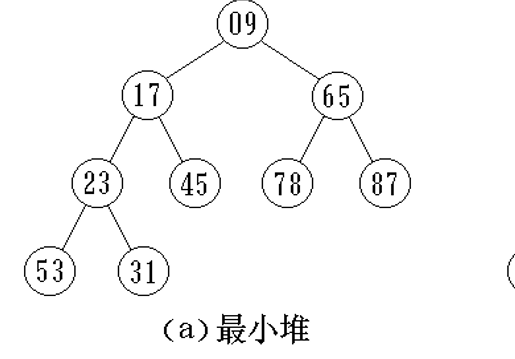
完全二叉树的数组表示
Ki <=K(2i+1) && Ki >= K(2i+2)
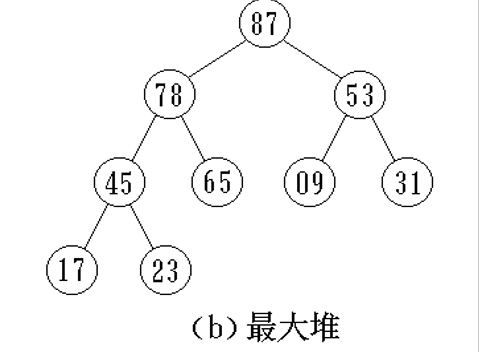
完全二叉树的数组表示
Ki >= K(2i+1) && Ki >= K(2i+2)
以最小堆为例
(最大堆部分代码参考第九章笔记下的:堆排序)
//最小堆的类定义
template <class Type> class MinHeap :
public MinPQ <Type> {
public:
MinHeap ( int maxSize );
MinHeap ( Type arr[ ], int n );
~MinHeap ( ) { delete [ ] heap; }
const MinHeap<Type> & operator =
( const MinHeap &R );
int Insert ( const Type &x );
int RemoveMin ( Type &x );
int IsEmpty ( ) const
{ return CurrentSize == 0; }
int IsFull ( ) const
{ return CurrentSize == MaxHeapSize; }
void MakeEmpty ( ) { CurrentSize = 0; }
private:
enum { DefaultSize = 10 };
Type *heap;
int CurrentSize;
int MaxHeapSize;
void FilterDown ( int i, int m );
void FilterUp ( int i );
}template <class Type> MinHeap <Type> ::
MinHeap ( int maxSize ) {//根据给定大小maxSize,建立堆对象
MaxHeapSize = DefaultSize < maxSize ?
maxSize : DefaultSize; //确定堆大小
heap = new Type [MaxHeapSize]; //创建堆空间
CurrentSize = 0; //初始化
}
//堆的建立
template <class Type> MinHeap <Type> ::
MinHeap ( Type arr[ ], int n ) {//根据给定数组中的数据和大小,建立堆对象
MaxHeapSize = DefaultSize < n ? n : DefaultSize;
heap = new Type [MaxHeapSize];
heap = arr; //数组传送
CurrentSize = n; //当前堆大小
int currentPos = (CurrentSize-2)/2; //最后非叶
while ( currentPos >= 0 ) { //从下到上逐步扩大,形成堆
FilterDown ( currentPos, CurrentSize-1 );
//从currentPos开始,到CurrentSize为止, 调整
currentPos--;
}
}
//最小堆的向下调整算法
template <class Type> void MinHeap<Type> ::
FilterDown ( int start, int EndOfHeap ) {
int i = start, j = 2*i+1; // j 是 i 的左子女
Type temp = heap[i];
while ( j <= EndOfHeap ) {
if ( j < EndOfHeap && heap[j].key >
heap[j+1].key ) j++; //两子女中选小者
if ( temp.key <= heap[j].key ) break;
else { heap[i] = heap[j]; i = j; j = 2*j+1; }
}
heap[i] = temp;
}
//堆的插入
template <class Type> int MinHeap<Type> ::
Insert ( const Type &x ) {
//在堆中插入新元素 x
if ( CurrentSize == MaxHeapSize ) //堆满
{ cout << "堆已满" << endl; return 0; }
heap[CurrentSize] = x; //插在表尾
FilterUp (CurrentSize); //向上调整为堆
CurrentSize++; //堆元素增一
return 1;
}
//最小堆的向上调整算法
template <class Type> void MinHeap<Type> ::
FilterUp ( int start ) {
//从 start 开始,向上直到0,调整堆
int j = start, i = (j-1)/2; // i 是 j 的双亲
Type temp = heap[j];
while ( j > 0 ) {
if ( heap[i].key <= temp.key ) break;
else { heap[j] = heap[i]; j = i; i = (i -1)/2; }
}
heap[j] = temp;
}
//最小堆的删除算法
template <class Type> int MinHeap <Type> ::
RemoveMin ( Type &x ) {
if ( !CurrentSize )
{ cout << “ 堆已空 " << endl; return 0; }
x = heap[0]; //最小元素出队列
heap[0] = heap[CurrentSize-1];
CurrentSize--; //用最小元素填补
FilterDown ( 0, CurrentSize-1 );
//从0号位置开始自顶向下调整为堆
return 1;
}
补充:函数指针
函数是一段程序,运行时与变量一样占用内存,也就有 一个起始地址,即指向此函数的指针。
函数指针定义格式: 类型名 (*函数名)(形参表)[=函数名];
如:若有函数:int fun(int,char);
则:int (*p)(int, char); p=fun;
或 int (* p)(int,char)=fun; //p为指向函数fun的指针
注:函数名为指针常量,不可改变;函数指针一般用作 函数参数,用来简化有规律的函数调用。 例:使用函数名作函数参数
#include <iostream.h>
int minus(int a,int b) {return a-b;}
int plus(int a,int b) {return a+b;}
int multiply(int a,int b) {return a*b;}
int divide(int a,int b) {return a/b;}
int op (int a, int b, int (*p)(int,int) ) { return p(a,b); }
void main( ) {
cout<<"5+3="<<op(5,3,plus)<<endl;
cout<<"5-3="<<op(5,3,minus)<<endl;
cout<<"5*3="<<op(5,3,multiply)<<endl;
cout<<"5/3="<<op(5,3,÷)<<endl; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号