数据结构笔记(第二章)
第二章:线性结构之线性表
数据的逻辑结构 :
-
集合
-
线性结构—>线性表、栈、队列、优先队列
-
树结构
-
图结构
线性表的存储结构 :
-
线性表的基于数组的存储表示叫做顺序表(SeqList),线性表的基于指针的存储表示叫做链表(LinkedList)(单链表、双链表、循环链表等)
-
数据的操作:插入、删除、修改、检索、排序等
-
注意其算法时间复杂度
顺序表(SeqList)
存储要点:
-
用一段地址连续的存储单元
-
依次存储线性表中的数据元素
用什么属性来描述顺序表:
-
存储空间的起始位置
-
顺序表的容量(最大长度)
-
顺序表的当前长度
顺序表的优点:
⑴ 无需为元素之间的逻辑关系而增加额外存储空间;
⑵ 随机存取:可以快速地存取表中任一位置的元素。
顺序表的缺点:
⑴ 插入和删除操作需要移动大量元素;
⑵ 表的容量难以确定,表的容量难以扩充;
⑶ 造成存储空间的碎片。
顺序表的静态存储和动态存储
#define maxSize 100
typedef int T;
typedef struct {
T data[maxSize]; //顺序表的静态存储表示
int n;
} SeqList;
typedef int T;
typedef struct {
T *data; //顺序表的动态存储表示
int maxSize, n;
} SeqList;
顺序表(SeqList)类的定义
const int defaultsize=100;
template <class T>
class SeqList: public LinearList<T> {
protected:
T *data; //顺序表存储数组
int MaxSize; //最大允许长度
int last; //当前最后元素下标
void reSize(int newSize);
public:
SeqList ( int sz= defaultSize );
SeqList(SeqList<T>& L);
~SeqList ( ) { delete [ ] data; }
int Size()const{return maxSize;}
int Length ( ) const { return last+1; }
int Search ( T& x ) const; //查找
int Locate ( int i ) const; //定位
bool getData(int i,T& x)const
{if(i>0&&i<=last+1) {x=data[i-1];return true; }
else return false;}
void setData (int i, T& x)
{if(i>0 && i<=last+1) { data[i-1]=x; }
int Insert (int i, T & x); //插入
int Remove (int i, T & x ); //删除
bool IsEmpty ( ) { return (last ==-1)?true:false; }
bool IsFull ( ) { return last == MaxSize-1?true:false; }
void input();
void output();
SeqList<T> operator=(SeqList<T>& L);
};
顺序表部分公共操作的实现
template <class T> //构造函数
SeqList<T> :: SeqList ( int sz ) {
if ( sz > 0 ) {
MaxSize = sz;
last = -1;
data = new T [MaxSize];
if ( data == NULL ) {
cerr<<"存储分配失败!"<<endl;
exit(1);
}
}
}
template <class T> //复制构造函数
SeqList<T> :: SeqList( SeqList<T>& L ){
maxSize=L.Size();
last=L.Length()-1;
T value;
data=new T[maxSize];
if ( data == NULL ) {
cerr<<"存储分配失败!"<<endl;exit(1);
}
for(int i=1;i<=last+1;i++)
{ L.getData(i,value);data[i-1]=value; }
}
template <class T> //重定义大小
void SeqList<T> :: reSize(int newSize){
if(newSize<=0){cerr<<"无效的数组大小"<<endl;return;}
if(newSize!=maxSize){
T *newarray=new T[newSize];
if ( newarray == NULL ) {
cerr<<"存储分配失败!"<<endl;exit(1); }
int n=last+1;
T *srcptr=data;
T *destptr=newarray;
while(n- -)*destptr++=*srcptr++;
delete []data;
data=newarray; maxSize=newSize;
}
}
template <class T>
int SeqList<T> :: search ( T & x ) const {
//搜索函数:在顺序表中从头查找结点值等于
//给定值x的结点所在位置,如果没找到返回0
for(int i = 0; i <= last ; i++)
if (data[i]==x) return i+1 ;
return 0;
}
template <class T> //顺序表的表项的插入insert算法
bool SeqList<T> :: Insert (T& x, int i )
{
if (last+1 >= MaxSize|| (i < 0 || i > last + 1) ) return false;
for (int j = last; j >= i; j- -) data[j+1] = data[j];
data[i] = x;
last++;
return true;
}
template <class T> //Remove:从顺序表中删除第i项,其值赋给x
bool SeqList<T> :: Remove ( int i, T& x ) {
//在表中删除已有元素 x
if(last==-1 ||i<1 || i>last+1) return false; x=data[i-1];
for ( int j = i; j <= last; j++ )
data[j-1] = data[j];
last- - ;
return true; //成功删除
}
template <class T> //顺序表的输入算法
void SeqList<T> ::input() {
cout<<“请输入元素个数减一";
while(1){
cin>>last;
if(last<=maxSize-1)break;
cout<<"个数输入有误";
}
cout<<“0:”<<endl;
for(int i=0;i<=last; i++)
{cin>>data[i]; cout<<i+1<<endl;}
}
template <class T> //顺序表的输出算法
void SeqList<T> ::output() {
cout<<"当前元素最后位置为"<<last+1<<endl;
for(int i=0;i<=last;i++)
{cout<<"#"<<i+1<<":"<<data[i]<<endl;}
}
顺序表的应用:集合的“并”运算
void Union ( SeqList<int> & A, SeqList<int> & B)
{
int n = A.Length ( ), x;
int m = B.Length ( );
for ( int i = 1; i < =m; i++ ) {
B.getData(i,x); //在B中取一元素
int k = A.Search (x); //在A中搜索它
if ( k == 0 ) //若未找到插入它
{ A.Insert (n, x); n++; }
}
}
void main(){
SeqList<int> s1,s2;
s1.input();
s2.input();
Union(s1,s2);
s1.output();
}
顺序表的应用:集合的“交”运算
void Intersection ( SeqList<int> & A,
SeqList<int> & B ) {
int n = A.Length ( );
int m = B.Length ( ); int i = 1, x;
while ( i < =n ) {
A.get Data(i, x); //在A中取一元素
int k = B.search (x); //在B中搜索它
if ( k == 0 ) { A.Remove (i,x); n- - ; }
//未找到在A中删除它
else i++;
}
}
测试后的一份完整代码
#include <stdio.h>
#include <assert.h>
#include <iostream>
#define DefaultSize 100
using namespace std;
template <class Type> class SeqList {
public:
SeqList( int size = DefaultSize ){
assert ( size >= 0 );
if ( size > 0 ) {
MaxSize = size; last = -1;
data = new Type[MaxSize];
}
}
~SeqList() { delete[] data; }
int Length() const { return last + 1; }
int Find( Type & x ) const;
int IsIn ( Type & x);
int Insert ( Type & x, int i );
int Remove ( Type & x);
int Next ( Type & x );
int Prior ( Type & x );
int IsEmpty() { return last == -1; }
int IsFull() { return last == MaxSize - 1; }
Type Get( int i ) { return i < 0 || i > last ? NULL:data[i]; }
void Print();
private:
Type *data;
int MaxSize;
int last;
};
/*template < class Type >
SeqList <Type>::SeqList( int size = DefaultSize ) {
assert ( size >= 0 );
if ( size > 0 ) {
MaxSize = size; last = -1;
data = new Type[MaxSize];
}
}
*/
template < class Type > int SeqList <Type>::Find( Type & x ) const {
int i = 0;
while ( i <= last && data[i] != x ) i++;
if ( i > last ) return -1;
else return i;
}
template < class Type > int SeqList <Type>::IsIn( Type & x ) {
int i = 0, found = 0;
while ( i <= last && !found)
if ( data[i] != x ) i++;
else found = 1;
return found;
}
template < class Type > int SeqList <Type>::Insert( Type & x, int i ) {
if ( i < 0 || i > last+1 || last == MaxSize - 1 ) return 0;
else {
last++;
for ( int j = last; j > i; j-- ) data[j] = data[j-1];
data[i] = x;
return 1;
}
}
template < class Type > int SeqList <Type>::Remove( Type & x ) {
int i = Find(x);
if ( i >= 0 ) {
last--;
for ( int j = i; j <= last; j++ ) data[j] = data[j+1];
return 1;
}
}
template < class Type > int SeqList <Type>::Next( Type & x ) {
int i = Find(x);
if ( i >= 0 && i < last ) return i+1;
else return -1;
}
template < class Type > int SeqList <Type>::Prior( Type & x ) {
int i = Find(x);
if ( i > 0 && i <= last ) return i-1;
else return -1;
}
template < class Type > void Union( SeqList <Type> & LA, SeqList <Type> & LB ) {
int n = LA.Length(); int m = LB.Length();
for ( int i=0; i <= m; i++ ) {
Type x = LB.Get(i);
int k = LA.Find(x);
if ( k == -1 ) { LA.Insert( x, n ); n++;}
}
}
template < class Type > void Intersection ( SeqList <Type> & LA, SeqList <Type> & LB ) {
int n = LA.Length(); int m = LB.Length(); int i = 0;
while ( i < n ) {
Type x = LA.Get(i);
int k = LB.Find(x);
if ( k == -1 ) { LA.Remove(x); n--; }
else i++;
}
}
template < class Type > void SeqList <Type>::Print() {
if ( last == -1 ) cout<<"It is empty" ;
else for ( int i=0; i<=last; cout << " data[" << i++ << "] = " << data[i] );
cout << endl;
}
int main(){
int length;
SeqList<int>* sq=new SeqList<int>;
cout<<"请输入元素个数";
cin>>length;
int result;
//cout<<length;
for(int i=1;i<=length;i++){
result=sq->Insert(i,i-1);
cout<<result<<endl;
}
sq->Print();
}
链表(Linked List)
单链表 (Singly Linked List)
单链表是最简单的链表,也叫线性链表,它用指针表示结点间的逻辑关系。特点:
- 每个元素(表项)由结点(Node)构成。数据域和指针域。

- 线性结构(first为头指针)

-
结点可以连续,可以不连续存储
-
结点数据元素顺序与物理顺序可能不一致。元素之间的逻辑关系用指针表示
-
表扩充很方便
单链表的类定义
多个类表达一个概念(单链表):
-
链表结点(ListNode)类型
-
链表(List)类型
定义两种类型关系的方式:
-
嵌套方式
-
继承方式
-
复合方式**
1、嵌套类(不合适)
class List { //链表类定义(嵌套方式)
public:
……… //链表操作
private:
class LinkNode { //嵌套链表结点类
public:
int data; //可被两个类的成员访问
LinkNode *link;
};
LinkNode *first ; //表头指针
};
2、继承方式(不合适)
链表类和链表结点类定义(继承方式)
class LinkNode { //链表结点类
protected:
int data;
LinkNode * link;
};
class List : public class LinkNode { //链表类, 继承链表结点类的数据和操作
private:
LinkNode *first; //表头指针
};
3、复合类
(友元类不具有对称性)
class List; //链表类定义(复合方式)
class LinkNode { //链表结点类
friend class List; //链表类为其友元类
private:
int data; //结点数据, 整型
LinkNode * link; //结点指针
};
class List { //链表类
private:
LinkNode *first; //表头指针
};
复合类2: 用struct定义linkNode类(最佳)
struct LinkNode { //链表结点类
int data;
LinkNode * link;
};
class List { //链表类
private:
LinkNode *first; //表头指针
public:
……
};//虽然结构使得LinkNode失去了封装性,但是所有属于List对象的LinkNode结点只能用first 进行访问
单链表中的插入与删除(part 1)
插入:单链表(a1,a2,a3……an)希望在ai之后插入新元素x
第一种情况:在第一个结点前插入
LinkNode* newnode=new LinkNode(x);
newnode->link = first ;
first = newnode;

第二种情况:在链表中间插入(p指向ai)
newnode->link = p->link;
p->link = newnode
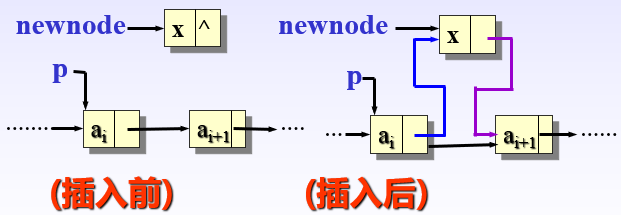
第三种情况:在链表末尾插入( p指向ai )
newnode->link = p->link;
p->link = newnode;

从上面的分析看出,后两种情况(即在表中间插入和在表尾插入)的操作是一样的,可以合并处理,但首节点前插入操作不同。(因为首节点没有前驱)
- 删除:在单链表中删除ai结点
第一种情况: 删除表中第一个元素
del=first;first=first->link;//del指向被删结点
delete del;
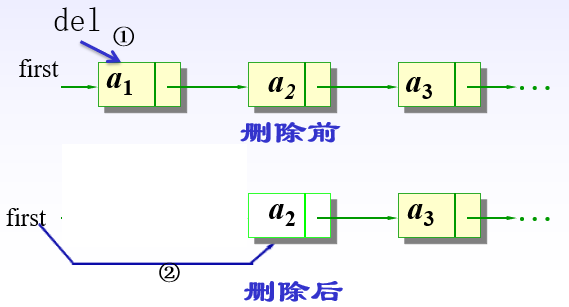
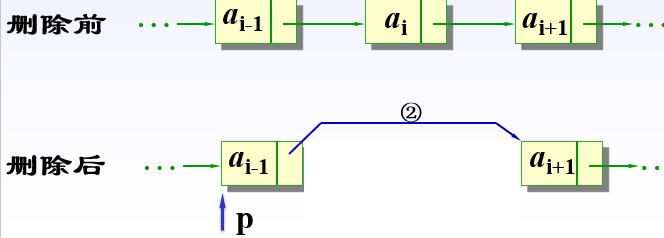
第二种情况: 删除表中或表尾元素
del=p->link;
p->link=del->link;
(或p->link=p->link->plink)
delete del;
// 用P指向被删结点前一个结点,del指向被删结点
单链表中的插入与删除(part 2)
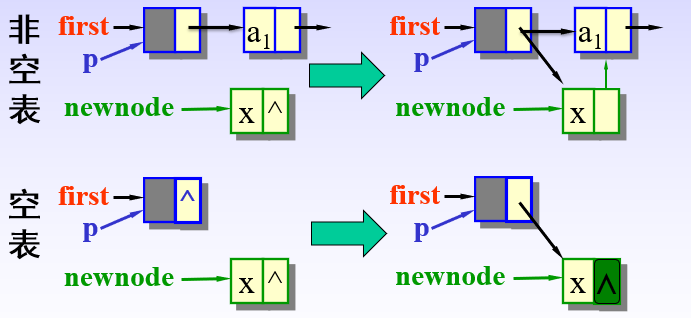
在带附加头结点的单链表第一个结点前插入新结点
newnode->link = p->link;
p->link = newnode;
// 在空表或非空表的第1个结点前插入可以统一操作
在带附加头结点的单链表中删除第一个结点
del = p->link;
p->link = del->link;
delete del;
// 用P指向被删结点前一个结点,del指向被删结点


带附加头结点的单链表类
template <class T> //结点结构定义
struct LinkNode {
T data; //结点数据
LinkNode<T> *link; //结点链接指针
LinkNode(LinkNode<T> *ptr=NULL ) {link=ptr; } // 仅初始化指针成员的构造函数
LinkNode (const T& item, LinkNode<T> *ptr=NULL ) {data=item;link=ptr;
}
};
template <class T> //链表类
class List :public LinearList<T>{
protected:
LinkNode<T> *first; //链表的头指针
public:
List () { first = new LinkNode<T>; }
List (const T& x) { first = new LinkNode<T> (x ); }
List (List<T>& L);
~List () { makeEmpty(); }
void MakeEmpty ( ); //将链表置为空表
int Length( )const; //计算链表的长度
LinkNode<T> *getHead()const { return first; }
LinkNode<T> *Search( T x );
//搜索含数据x的元素
LinkNode<T> * Locate( int i );
//搜索第 i 个元素的地址
bool GetData ( int i, T& x );
//取出表中第 i 个元素的值
bool Insert (int i ,T& x);
//将x插在表中第 i 个元素后
bool Remove (int i ,T& x);
//删除第i个元素,x返回该元素的值
bool IsEmpty()const
{ return first->link==NULL?true:false; }
bool IsFull() const {return false;}
void Sort();
void input();
void output();
List<T>& operator=(List<T>& L);
}; //list类定义到此结束
链表类部分操作的实现
template <class T>
List <T> ::List(List<T>& L) { //复制构造函数
T value;
LinkNode<T> *srcptr=L.getHead();
LinkNode<T> *destptr=first=new LinkNode<T>;
while ( srcptr->link != NULL ) {
value=srcptr->link->data;
destptr->link=new LinkNode<T>(value);
destptr=destptr->link;
srcptr = strptr->link;
}
destptr->link=NULL;
}
template <class T> //置空表
void List <T> :: MakeEmpty ( ) {
//删去链表中除附加头结点外的所有其他结点
//即把表变为有附加头结点的空表
LinkNode<T> *q;
while ( first->link != NULL ) {
q = first->link; first->link = q->link; //将表头结点后第一个结点q从链中摘下
delete q; //释放它
}
}
template <class T>//链表长度
int List<T> :: Length ( ) const {
//求单链表的长度
LinkNode<T> *p = first->link;
//检测指针 p 指示第一个结点
int count = 0;
while ( p != NULL ) { //逐个结点检测
count++;
p = p->link;
}
return count; //注意count的初始化和返回值之间的关系
}
template <class T> //搜索
LinkNode<T> *List <T> :: Search (T x ) {
//在链表中从头搜索其数据值为x的结点
LinkNode<T> * p = first->link;
//检测指针 p 指示第一个结点
while ( p != NULL )
if ( p->data == x ) break;
else p = p->link;
return p;
// p 在搜索成功时返回找到的结点地址
// p 在搜索不成功时返回空值
}
template <class T> //定位
LinkNode<T> *List<T> :: Locate ( int i ) {
//定位函数。返回表中第 i 个元素的地址
//若 i < 0或 i 超出,则返回NULL
if ( i < 0 ) return NULL; // i 值不合理
LinkNode<T> * p =first;
int k = 0;
while ( p != NULL && k < i )
{p = p->link ; k++;} //找第 i 个结点
return p; //返回第 i 个结点地址或NULL
}
template <class T> //取值
bool * List<T> :: GetData ( int i, T& x ) {
//取出链表中当前元素的值
if (i<=0) return NULL;
LinkNode<T> *p = Locate ( i );
// p 指向链表第 i 个结点
if ( p == NULL )
return false;
else { x=p->data; return true; }
}
template <class T> //单链表的实现———插入
bool LinkList<T> :: Insert(int i, T& x) //在第i个位置后插入x
{
LinkNode<T> * p=Locate(i);
if (p == NULL) return false ; //没有找到
else {
s = new LinkNode<T>(x); //申请一个结点s
if(s==null){cerr<<"store is error"<<endl; exit(1);}
s->link= p->link;
p->link = s; //结点s插入结点p之后
return true;
}
}
template <class T> //删除
bool List<T> :: Remove ( int i ,T& x)
{
LinkNode<T> *p = Locate (i-1);
if (p == NULL || p->link == NULL) return false;
LinkNode<T> *q= p->link;
x = q->data;
p->link = q->link;
delete q;
return true;
}
template <class T> //重载
List<T>& List<T> :: Operator= (List<T>& L) {
//赋值操作,A=B,A是调用者,B是实参
T value;
LinkNode<T> *srcptr=L.getHead();
LinkNode<T> *destptr=first=new LinkNode<T>;
while ( srcptr->link != NULL ) {
value=srcptr->link->data;
destptr->link=new LinkNode<T>(value);
destptr=destptr->link;
srcptr = strptr->link;
}
destptr->link=NULL;
return * this;//加此句是使得表达式"A=B"的值为A,可做连续赋值 }
template <class T> //前插法建立单链表
void List <T> :: inputFront (T endTag ) {
LinkNode<T> *newNode; T val;
makeEmpty();
cin>>val;
while (val != endTag) {
newNode = new LinkNode<T>(val);
if(newNode==NULL)
{cerr<<"error"<<endl;exit(1);}
newNode->link=first->link;
first->link=newNode;
cin>>val;
} }
template <class T> //后插法建立单链表
void List <T> :: inputRear(T endTag ) {
LinkNode<T> *newNode,*last,T val;
makeEmpty();
cin>>val; last=first;
while (val != endTag) {
newNode = new LinkNode<T>(val);
if(newNode==NULL)
{cerr<<"error"<<endl;exit(1);}
last->link=newNode;
last=newNode;
cin>>val;
} }
单向循环链表(简称循环链表)
循环链表1:将单链表的首尾相接,将终端结点的指针域由空指针改为指向开始结点,构成单循环链表,简称循环链表。
循环链表2:带尾指针的循环链表,在循环链表里设置last不仅仅有利于插入,删除也很方便。所以,在后面的循环链表的定义里,封装了两个指针first和last
循环链表3: 要使空表和非空表的处理一致,可附设头结点**
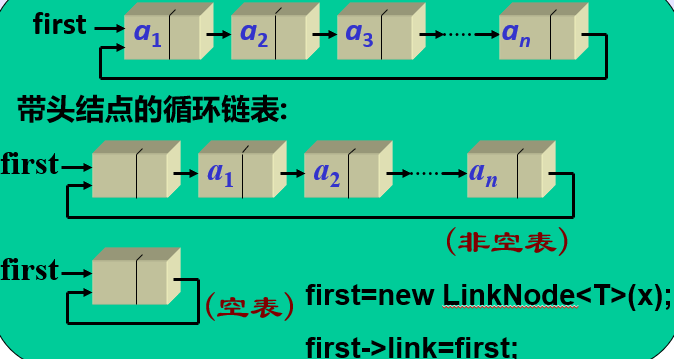
循环链表中没有明显的尾端,如何避免死循环?
循环条件:
(单链表)p != NULL->p != first (循环链)
(单链表)p->link != NULL->p->link != first(循环链)
循环链表类的定义
template <class T> //结点定义
struct CircLinkNode {
T data; //结点数据
CircLinkNode<T> *link; //链接指针
CircLinkNode ( CircLinkNode<T> *next = NULL ) :
link ( next ) { }
CircLinkNode ( T d ,CircLinkNode<T> *next = NULL ) : data ( d ), link ( next ) { }
};
template <class T>
class CircList :pulic LinearList<T> {
private:
CircLinkNode<T> *first, *last;
//链表的表头指针、当前指针和表尾指针
public:
CircList ( const T& x );
CircList ( CircList<T>& L);
~CircList ( );
int Length ( ) const;
bool IsEmpty ( ) { return first->link == first; }
CircLinkNode<T> * getHead( )const;
void setHead(CircLinkNode<T> *p);
CircLinkNode<T> * Search(T x);
CircLinkNode<T> * Locate(int i);
T *getData ( int i );
void setData( int i, T& x);
bool Insert (int i, T& x );
bool Remove (int i, T& x );
};
//循环链表与单链表的操作实现,最主要的不同就是扫描到链尾,遇到的不是NULL,而是表头first
循环链表类部分操作的实现
template <class T> //循环链表的搜索算法
CircListNode<T> * CircList<T>::Search( T x )
{
//在链表中从头搜索其数据值为 x 的结点
current = first->link;
while ( current != first && current->data != x )
current = current->link;
return current;
}
template <class T> //循环链表——插入
bool CircList<T> ::Insert(int i, T x)//在i项后面插入一项
{ if i<0 return false;
CircLinkNode<T> * p ; int count;
if (i==0) {p=first;count=0}else{ p=first->link; count=1;}
//第一个位置特别处理。避免指针出界状态与初始状态重合
while (p != first && count < i )
{
p = p->link; count++;
}
if (p == first&&i!=0) return false;
else {
s = new CircLinkNode<T>; s->data = x;
s->link = p-> link; p-> link = s;
return true;
}
}
//循环链表,循环指针结束条件不同于单链表,所以初始化不同。需要特别考虑第一个元素
用循环链表求解约瑟夫问题
约瑟夫问题的提法
n 个人围成一个圆圈,首先第 1 个人从 1 开始一个人一个人顺时针报数, 报到第 m 个人,令其出列。然后再从下一 个人开始,从 1 顺时针报数,报到第 m 个人,再令其出列,…,如此下去, 直到圆圈中只剩一个人为止。此人即为优胜者。
1、带头结点的完整代码
#include <iostream>
using namespace std;
template <class T> //结点定义
struct CircLinkNode {
T data; //结点数据
CircLinkNode<T> *link; //链接指针
CircLinkNode ( CircLinkNode<T> *next = NULL ):link ( next ) { }
CircLinkNode ( T d,CircLinkNode<T> *next = NULL ):data(d), link(next) { }
};
template <class T>
class CircList{
private:
CircLinkNode<T> *first, *last;//链表的表头指针、当前指针和表尾指针
public:
CircList(){first=new CircLinkNode<T>(); first->link=first;};
//CircList ( const T& x );
// CircList ( CircList<T>& L);
// ~CircList ( );
// void setHead(CircLinkNode<T> *p);
// CircLinkNode<T> * Search(T x);
// CircLinkNode<T> * Locate(int i);
// T *getData ( int i );
// void setData( int i, T& x);
bool insert (int i, T& x );
// bool Remove (int i, T& x );
//bool IsEmpty ( ) { return first->link == first; }
// int Length ( ) const;
CircLinkNode<T> * getHead( )const{return first;};
//void input(int i); //输入i个元素
};
template <class T>
bool CircList<T>::insert(int i, T& x)//在i项后面插入一项
{ if(i<0)return false;
CircLinkNode<T> * p,s ;
int count ;
if(i==0) {p=first;count=0;}
else {p=first->link;count=1;} //第一个位置特别处理。避免循环指针出界状态与初始状态重合
while (p != first && count < i )
{
p = p->link;
count++;
}
if (p == first&&i!=0) return false;
else {
// s = new CircLinkNode<T>(); s->data = x;
// s->link = p->link; p->link = s;
p->link=new CircLinkNode<T>(x,p->link);
cout<<"input:"<<x<<endl;
return true;
}
}
template <class T>
void Josephus(CircList<T>& Js, int n, int m) {
CircLinkNode<T> *p,*first, *pre = NULL;
first= Js.getHead();
p=first->link;
if(p==first) exit(1); //表空退出
int i, j;
for ( i = 0; i < n-1; i++ ) { //执行n-1次
if(p==first)p=p->link;
for ( j = 1; j < m; j++) //数m-1个人
{
pre = p; p = p->link;
if(p==first)j--;
}
cout << "出列的人是" << p->data << endl;
pre->link = p->link; delete p; //删去
p = pre->link;
}
};
void main() {
CircList<int> clist;
int i,n,m;
cout << "输入游戏者人数和报数间隔 : ";
cin >> n >> m;
for (i = 1; i <= n; i++ ) clist.insert(i-1, i); //约瑟夫环
// inclist.input(n); //函数需考虑第一个元素插入的特殊性
Josephus(clist, n, m); //解决约瑟夫问题
}
2 不带头结点的完整代码
#include <iostream>
using namespace std;
template <class T> //结点定义
struct CircLinkNode {
T data; //结点数据
CircLinkNode<T> *link; //链接指针
CircLinkNode ( CircLinkNode<T> *next = NULL ):link ( next ) { }
CircLinkNode ( T& d,CircLinkNode<T> *next = NULL ):data(d), link(next) { }
};
template <class T>
class CircList{
private:
CircLinkNode<T> *first, *last;//链表的表头指针、当前指针和表尾指针
public:
CircList(){first=last=NULL;}
//CircList ( const T& x );
// CircList ( CircList<T>& L);
// ~CircList ( );
// void setHead(CircLinkNode<T> *p);
// CircLinkNode<T> * Search(T x);
// CircLinkNode<T> * Locate(int i);
// T *getData ( int i );
// void setData( int i, T& x);
// bool insert (int i, T& x );
// bool Remove (int i, T& x );
//bool IsEmpty ( ) { return first->link == first; }
// int Length ( ) const;
CircLinkNode<T> * getHead( )const{return first;};
void input(int i); //从空表开始,输入i个元素
};
template <class T>
void CircList<T>::input(int i)//插入i项
{ if(i<=0) return;
//makeEmpty(); 清空原表
T temp;
cin>>temp;
first=last=new CircLinkNode<T>(temp); first->link=first; //特别处理第一个元素
cout<<"输入元素"<<temp<<endl;
for(int j=2;j<=i;j++)
{
cin>>temp;
last->link=new CircLinkNode<T>(temp,last->link);
last=last->link;
cout<<"输入元素"<<temp<<endl;
}
}
template <class T>
void Josephus(CircList<T>& Js, int n, int m) {
CircLinkNode<T> *p,*first, *pre = NULL;
p=first= Js.getHead();
if(first==NULL) exit(1); //表空退出
int i, j;
for ( i = 0; i < n-1; i++ ) { //执行n-1次
for ( j = 1; j < m; j++) //数m-1个人
{
pre = p; p = p->link;
}
cout << "出列的人是" << p->data << endl;
pre->link = p->link; delete p; //删去
p = pre->link;
}
};
void main() {
CircList<int> clist;
int n,m;
cout << "输入游戏者人数和报数间隔 : ";
cin >> n >> m;
//for (i = 1; i <= n; i++ ) clist.insert(i-1, i); //约瑟夫环
clist.input(n); //函数需考虑第一个元素插入的特殊性
Josephus(clist, n, m); //解决约瑟夫问题
}
双向循环链表(简称双链表)
双向链表简称双链表,为了解决链表在前驱和后继方向都能遍历的线性链表。
双向链表通常采用带附加头结点的循环链表形式。
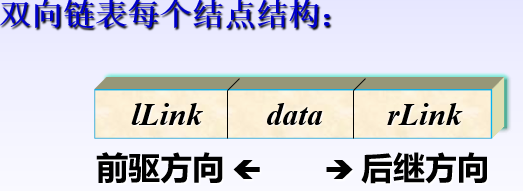
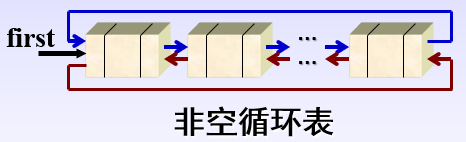
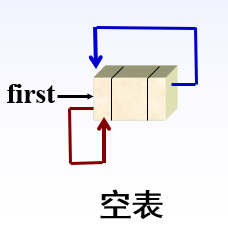
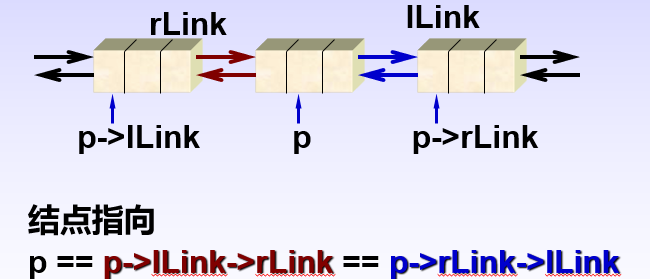
双向循环链表类的定义
template <class T>
struct DblNode { //链表结点的定义
T data; //数据
DblNode<T> * lLink, * rLink; //指针
DblNode( DblNode<T> * left=NULL, DblNode<T> * right =NULL ) : lLink (left), rLink (right){ }
DblNode (T value, DblNode<T> * left=NULL,
DblNode<T> * right=NULL ) :
data (value), lLink (left), rLink (right) { }
};
template <class T>
class DblList:Public LinearList<T> {
private:
DblNode<T> * first;
public:
DblList ( T uniqueVal ); //构造函数
~DblList ( ); //析构函数
int Length ( ) const; //计算长度
bool IsEmpty ( ) //判链表空否
{ return first->rlink == first; }
DblNode<T>* getHead( )const {return first; }
void setHead(DblNode<T> *ptr){ first=ptr; }
DblNode<T>* Search(const t& x);
//沿后继方向寻找等于x的结点
DblNode<T> *Locate(int i, int d);
//定位序号为i的结点,
//d=0按前驱方向,否则按后继方向
void Insert (int i, T& x,int d );
//在第i个结点后插入一个包含值x的新结点
bool Remove (int i, T& x,int d ); //删除第i个结点
};
双向循环链表的部分实现
template <class T> //-定位算法
DblNode<T>* DblList::Locate(int i,int d) {
//定位第i个结点, d=0为前驱方向,否则为后继方向。
if(i<0) return NULL;
if(i==0)return first ;
DblNode<T> * current ;
if(d==0) current=first->lLink;
else current=first->rLink;
for(int j=1;j<i;j++)
if ( current == first ) break; //越界
else if(d==0) current = current->lLink;
else current = current->rLink;
if(current != first) return current;
else return NULL ;
}
//删除算法(非空表)
current->rLink->lLink = current->lLink;
current->lLink->rLink = current->rLink;
delete current ;
注意双向链表的插入:
双向循环链表的插入分前驱方向的插入和后继方向的插入。
要求在第i个结点之后插入新结点NewNode,则
1.后继方向:从前往后找第i个结点current,在current之后插入NewNode
2.前驱方向:从后往前找第i个结点current,在current之前插入NewNode。
静态链表
静态链表:用数组来表示单链表,用数组元素的下标来模拟单链表的指针。
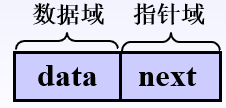
data:存储放数据元素;
next:也称游标,存储该元素的后继在数组的下标。
静态链表的结构

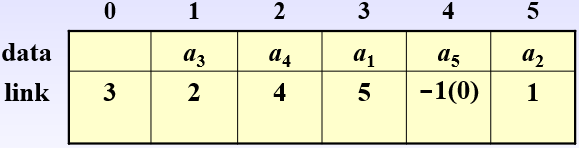
0号是表头结点,link给出首元结点地址。
循环链表收尾时link = 0,回到表头结点。如果不是循环链表,收尾结点指针link=-1。
link指针是数组下标,因此是整数。
//静态链表的存储结构定义如下:
const int MaxSize = 100; //100只是示例数据
template <class DataType>
struct SNode
{
DataType data; // DataType表示不确定的数据类型
int next; //指针域(也称游标)
} SList[MaxSize];
静态链表的应用——多项式 (Polynomial)
n阶多项式 Pn(x) 有 n+1 项。
系数 a0, a1, a2, …, an
指数 0, 1, 2, …, n。按升幂排列
多项式的存储表示:
//1.用一维静态数组表示,下标就是指数,值是系数
private:
int degree;
float coef [maxDegree+1];
Pn(x)可以表示为:
pl.degree = n
pl.coef[i] = ai //0=<i<=n
//2.用一维动态数组存储多项式的系数,下标即指数
private:
int degree;
float * coef;
Polynomial::Polynomial (int sz) {//在构造函数里初始化并分配空间。
degree = sz;
coef = new float [degree + 1];
}
//以上两种存储表示适用于指数连续排列的多项式。对于指数跳跃很大的稀疏多项式来说则太浪费空间了。
//3.设一元多项式多大可能阶为maxDegree,当前的多项式的最高阶为n。数组元素存放非零项的系数和指数,下标不再是指数
//4.用链表表示多项式,每个项term为如下结构:
Term |coef|exp|link|
优点是: 多项式的项数可以动态地增长,不存在存储溢出问题,也不浪费空间。 插入、删除方便。
多项式(polynomial)类的链表定义:
struct Term { //多项式结点定义
float coef; //系数
int exp; //指数
Term *link; //链接指针
Term (float c, int e, Term *next = NULL)
{ coef = c; exp = e; link = next;}
Term *InsertAfter ( float c, int e);
friend ostream& operator << (ostream&,
const Term& );
};
Term *Term::InsertAfter ( float c, int e ) {
//在调用此函数的对象后插入一个新项
link = new Term (c, e, link);
//创建一个新结点,自动链接
//插入到this结点后面
return link;
};
class Polynomial { //多项式类的定义
public:
Polynomal() { first = new Term(0, -1); } //构造函数
Polynomal ( Polynomal& R); //复制构造函数
int maxOrder(); //计算最大阶数
private:
Term *first;
friend ostream& operator << (ostream&,
const Polynomal& );
friend istream& operator >> ( istream&,
Polynomal& );
friend Polynomial operator + ( Polynomial& A, Polynomial& B );
friend Polynomial operator * ( Polynomial& A, Polynomial& B);
};
多项式的相加:
Polynomial operator +
(Polynomial & A, Polynomial & B) {
Term *pa, *pb, *pc, *p;
float temp;
Polynomal C;
pc=C.getHead( );
pa = A.getHead( )->link;
pb = B.getHead( )->link; //检测指针pa和pb都指
//向自己所指多项式链表第一个结点
while ( pa!=NULL && pb!=Null ){①
if(pa->exp==pb->exp){②
temp=pa->coef+pb->coef;
if (fabs(temp)>0.001)
pc=pc->InsertAfter(temp,pa->exp);
pa=pa->link; pb=pb->link; ②}
else if(pa->exp < pb->exp) {③
pc=pc->InsertAfter(pa->coef, pa->exp);
pa=pa->link ;
} ③
else {④
pc=pc->InsertAfter(pb->coef, pb->exp) ;
pb=pb->link;
} ④
} ①
//以下代码是把余下的A或B部分链到C的后面。
if(pa!=NULL) p=pa;
else p=pb;
while(p!=NULL)
{
pc=pc->InsertAfter(p->coef, p->exp);
p=p->link;
}
return C;
}
限于篇幅,有些知识点没有列出来,感觉以上这些是比较重要一点的东西。emmm,写博客也不需要面面俱到吧(努力为偷懒找借口)qwq。


