信息增益与KL散度
(一)前言
- 早就耳闻$KL$散度$(Kullback-Leibler$ $divergence)$大名,一方面近日回归分析课上提到了一些,但还是似懂非懂,另一方面又在重温随机森林时不可避免地进一步了解了信息增益的相关性质,而信息增益与$KL$散度之间的联系之紧密是不言而喻的,故想整合收集到的资料来学习一下这方面的知识
(二)定义与性质
- 熵:$H(X)\overset{def}{=}E_X[\ln \frac{1}{p(x)}]$
- 联合熵:$H(X,Y)\overset{def}{=}E_{X,Y}[\ln \frac{1}{p(x,y)}]$
- 条件熵:$H(Y\vert X)\overset{def}{=}E_X[E_{Y\vert X}[\ln \frac{1}{p(y\vert x)}]]$
- 性质:
- $H(X,Y)= -\iint p(x,y) \ln p(x,y) dx dy\\=-\iint p(x,y)\ln p(x) dx dy-\iint p(x,y) \ln p(y \vert x) dx dy\\=H(X)-\int p(x) \int p(y\vert x)\ln p(y \vert x) dy dx\\=H(X)+H(Y\vert X)$
- $H(X,Y)=H(Y)+H(X\vert Y)$
- 性质:
- $KL$散度:$D_{KL}(P\Vert Q)\overset{def}{=}-\int P(x)\ln \frac{Q(x)}{P(x)} dx$
- 信息增益:$I(X,Y)\overset{def}{=}D_{KL}(p(x,y)\Vert p(x)p(y))$
- 性质1:$I=H(Y)-H(Y\vert X)\\=H(X)-H(X\vert Y)\\=H(X)+H(Y)-H(X,Y)\\=H(X,Y)-H(Y\vert X)-H(X\vert Y)$
- 只需要证明第一个等号
- $I(X,Y)=\iint p(x,y) \ln \frac{p(x,y)}{p(x)p(y)}dxdy\\=\iint p(x,y) \ln \frac{p(x,y)}{p(x)}dxdy-\iint p(x,y) \ln p(y)dxdy\\=\int p(x)(\int p(y\vert x) \ln p(y \vert x) dy)dx-\int p(y) \ln p(y)dy\\=H(Y)-H(Y\vert X)$
- 具体理解如下图:
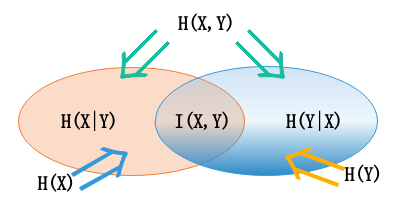
-
- 性质2:$I \geq 0$(此处证明更强的结论:$D_{KL}(P\Vert Q)$非负)
- 引理:设$\phi$为凸,且非负函数$f$满足$\int_{\Omega}f(t)dt=1$,则$\int_{\Omega} \phi(g(t))f(t) dt \geq \phi(\int_{\Omega}g(t)f(t) dt)$
- 证明:$D_{KL}(p\Vert q)=\int p(t)(-\ln \frac{q(t)}{p(t)}) dt \geq -\ln (\int \frac{q(t)}{p(t)} p(t) dt )=-\ln(1)=0$
- 性质3:$I$表示类别$X$(或$Y$)和类别$X\vert Y$(或$Y \vert X$)关于特征$Y$(或$X$)的平均散度
- 理由:$I(X,Y)=\int p(y) \int p(x\vert y)\ln \frac{p(x\vert y)}{p(x)}dxdy= E_Y[D_{KL}(p(x\vert y) \Vert p(x))]$



