论文记载:A Survey on Traffic Signal Control Methods
ABSTRACT
交通信号控制是一个重要且具有挑战性的现实问题,其目标是通过协调车辆在道路交叉口的移动来最小化车辆的行驶时间。目前使用的交通信号控制系统仍然严重依赖过于简单的信息和基于规则的方法,尽管我们现在有更丰富的数据、更强的计算能力和先进的方法来推动智能交通的发展。随着人们对使用机器学习方法(如强化学习)的智能交通越来越感兴趣,本调查涵盖了广泛认可的交通方法和交通信号控制强化的最新文献综合列表。我们希望这项调查能促进这一重要课题的跨学科研究。
1 INTRODUCTION
交通拥堵是一个日益严重的问题,它继续困扰着城市地区,给出行的公众和整个社会带来负面影响。随着越来越多的人涌向城市,这些负面结果只会越来越多。2014年,交通拥堵导致美国人损失了超过1600亿美元的生产力,浪费了超过31亿加仑的燃料[经济学人2014]。交通拥堵也归因于2011年超过560亿磅的有害CO2排放[Schrank等人,2015年]。在欧盟,交通拥堵的成本相当于整个国内生产总值的1%。缓解拥堵将带来显著的经济、环境和社会效益。信号交叉口是城市环境中最常见的瓶颈类型之一,因此交通信号控制在城市交通管理中起着至关重要的作用。
1.1 Current Situation
在今天的许多现代城市,广泛使用的自适应交通信号控制系统,如SCATS [Lowrie 1992]和SCOOT [Hunt等人1982,1981]严重依赖人工设计的交通信号计划。这种手动设置的交通信号计划被设计成根据环路检测到的交通量来动态选择传感器。然而,许多交叉口没有安装环路传感器,或者环路传感器维护不善。此外,环路传感器只有在车辆经过时才会被激活;因此,他们只能通过它们提供有关车辆的部分信息。因此,信号不能感知和反应实时交通模式。在某些交通状况下,工程师需要手动更改信号控制系统中的交通信号时序。图1显示了中国一个城市的十字路口的交通信号定时,无论全天的实际交通变化如何,交通信号定时很少变化。

1.2 Opportunities
首先,今天我们可以从各种来源收集到更丰富的信息。传统的交通信号控制依赖于环路传感器的数据,环路传感器只能感知车辆通过。然而,新的数据源很快变得可用,可以作为交通信号控制的输入。例如,用于安全目的的临街监控摄像头还可以提供附近道路交通状况的更详细描述,特别是车道上有多少辆车在等待,有多少辆车在轮流,它们位于哪里,以及它们行驶的速度有多快。此外,可以从各种来源收集大规模轨迹数据,例如导航应用(例如,Google Maps)、拼车平台(例如,Uber)以及与附近基础设施共享信息的配备GPS的车辆(例如,互联网车辆)。这些数据让我们对车辆如何到达十字路口有了更多的了解。我们已经达到了一个充分的移动信息阶段,可以更清楚地描述城市的交通动态,这是我们改善交通控制系统的一个重要资源。
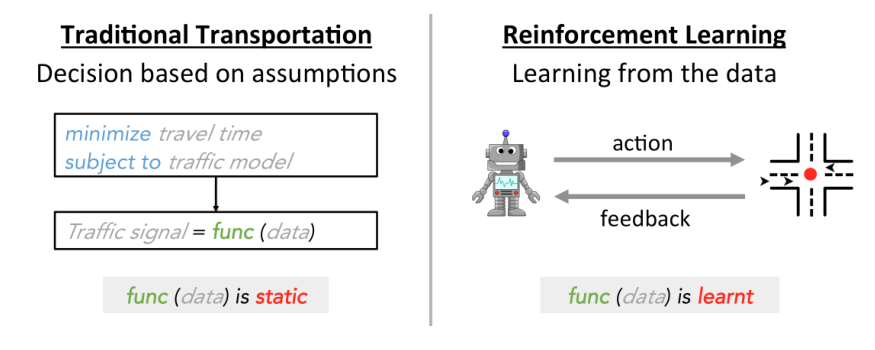
第二,今天我们拥有更强大的计算能力和先进的计算模型。交通研究人员采用的典型方法是在关于交通模型的某些假设下,将交通信号控制作为一个优化问题,例如,车辆以统一且恒定的速度行驶,[Roess et al.2004]为了使优化问题易于处理,必须做出各种(有时是强有力的)假设。这里的关键问题是,这些假设偏离了现实世界,而且往往偏离得很大。众所周知,现实世界的交通状况以一种复杂的方式发展,受到许多因素的影响,如驾驶员的偏好、与弱势道路使用者(如行人、骑自行车的人等)的相互作用。),天气和路况。这些因素很难用一个交通模型来完全描述。
另一方面,机器学习技术可以直接从观察到的数据中学习,而不会对模型做出不切实际的假设。然而,典型的监督学习在这里并不适用,因为现有的交通信号控制系统遵循预定义的信号计划,所以我们没有足够的训练数据来区分好的和坏的交通信号计划策略。相反,我们必须首先采取行动改变信号计划,然后从结果中学习。这种试错法也是强化学习(RL)的核心思想。本质上,RL系统基于当前环境生成并执行不同的策略(例如,用于交通信号控制)。然后,它将根据环境的反馈来学习和调整策略。这揭示了运输方法和我们的RL方法之间最显著的差异,如图2所示:在传统的运输研究中,模型func(数据)是静态的;在强化学习中,模型是在真实环境中通过试错法动态学习的。
1.3 Motivation of This Survey
随着人工智能技术的激增和城市数据的日益可用,政府和行业现在正积极寻求改善交通系统的解决方案。比如在中国,阿里巴巴和滴滴出行正在致力于利用移动数据和先进计算技术提升城市交通[CNN 2019;Wire 2018]。这项调查可以为业界提供一个有用的参考时,他们革命性的现行交通信号控制系统,试验基于RL的方法。具体来说,我们讨论了最近的基于学习的方法的学习方法及其优缺点,并对现有工作的实验设置进行了基准测试。
与此同时,随着强化学习技术最近的成功,我们看到学术界对使用强化学习来改善交通信号控制越来越感兴趣[曼尼恩等人,2016]。然而,大多数现有的机器学习方法倾向于忽略经典的运输方法,并且缺乏与现有运输方法的良好比较。这项调查综合考虑了机器学习和运输工程,并希望促进这一跨学科的研究方向。
1.4 Scope of This Survey
在本调查中,我们将涵盖交通信号控制中的许多经典或广泛接受的运输方法。我们建议对综合运输方法感兴趣的读者参考[李等2014;Papageorgiou等人,2003年;Roess等人,2004年]。强化学习方法在交通信号控制中的应用相对较新。深度强化学习的最新进展也引发了逆向学习在交通信号控制问题中的新应用。虽然[Yau等人2017]和[曼尼恩等人2016]主要对深度强化学习普及之前的早期研究进行了全面调查,但在本次调查中,我们将全面涵盖基于反向链路的交通信号控制方法,包括基于反向链路的交通信号控制方法的最新进展。
2 PRELIMINARY
2.1 Term Definition
道路结构和交通运行术语:
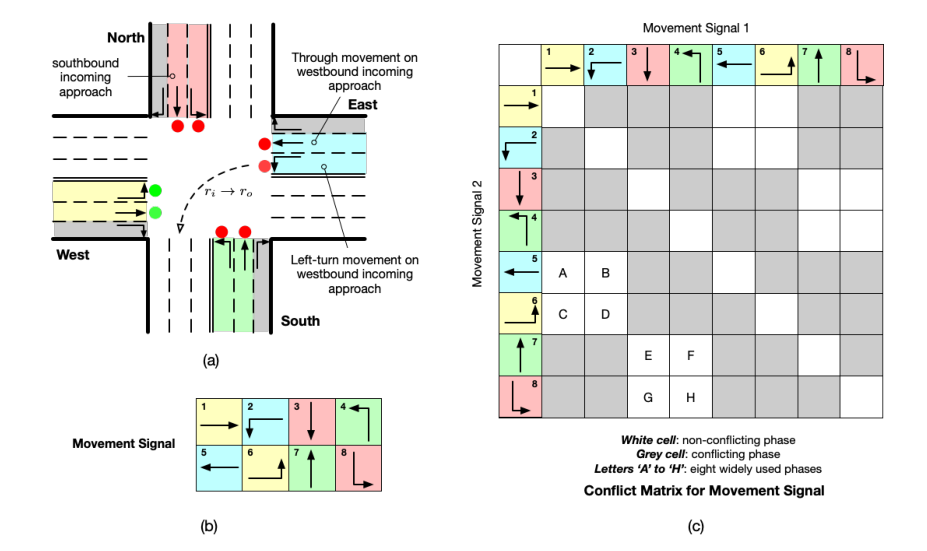
Approach(路口):在交叉路口相遇的道路被称为道路。在任何一般的交叉路口,都有两种路口: 进路和出路。一个进路是汽车可以进入十字路口的地方;出路是汽车可以离开十字路口的地方。图3(a)显示了一个典型的交叉路口,有四个进路和四个出路。在此图中,南行进路被表示为车辆沿南行方向行驶的北侧进路。
Lane(车道):一个路口由一组车道组成。类似于路口定义,有两种车道:进线车道和出线车道(在一些参考文献中也称为进/进线车道和收/出线车道[El-Tantawy和Abdulhai 2012斯蒂凡诺维奇[2010])。
Traffic movement(交通移动):交通移动是指车辆从一个进路移动到一个出路,定义为 \((r_i→ r_o)\) ,其中 \(r_i\) 和 \(r_o\) 分别表示进路和出路。交通移动通常分为左转、直行和右转。
交通信号术语:
Movement signal(移动信号):在交通移动上定义了移动信号,绿色信号表示允许相应的移动,红色信号表示禁止移动。对于图3(a)所示的四条支路的交叉口,无论信号如何,右转移动都可以通过,并且有八个移动信号在使用,如图3(b)所示。
Phase(相位):相位是移动信号的组合。图3(c)显示了图3(a)和图3(b)示例中两个移动信号组合的冲突矩阵。灰色单元格表示相应的两个移动相互冲突,即它们不能同时设置为“绿色”(例如,信号#1和#2)。白色单元格表示不冲突的移动信号。所有非冲突信号将产生八个有效的成对信号相位(图3(c)中的字母“A”至“H”)和八个单信号相位(冲突矩阵中的对角线单元)。这里我们只对成对信号相位进行字母编码,因为在单独的交叉口,使用成对信号相位总是更有效。当考虑多个交叉口时,单信号相位可能是必要的,因为潜在的回溢。
Phase sequence(相位序列):相位序列是定义一组相位及其变化顺序。
Signal plan(信号计划):单个交叉口的信号计划是一系列相位及其相应的起始时间。这里我们将信号计划表示为\((p_1,t_1)(p_2,t_2)...(p_i,t_i)...,\)其中 \(p_i\) 和 \(t_i\) 分别表示一个相位及其开始时间。
Cycle-based signal plan(基于周期的信号计划):基于周期的信号计划是一种信号计划,其中相位序列以循环顺序操作,可以表示为$(p_1,t1_1)(p_2,t1_2)...(p_N,t^1_N) $$(p_1,t2_1)(p_2,t2_2)...(p_N,t2_N)...$,其中$p_1,p_2,...p_N$是重复的相位序列,$tj_i$ 是第 \(j\) 个周期中相位 \(p_i\) 的开始时间。具体来说,\(C^j = t^{j+1}_1-t^j_1\)是第 \(j\) 个相位周期的周期长度,而\(\{\frac{t^j_2-t^j_1}{C^j},...,\frac{t^j_N-t^j_N}{C^j}\}\)是第 \(j\) 个相位周期的每一个相位所占比例。现有的交通信号控制方法通常全天重复类似的相位序列。
2.2 Objective
交通信号控制的目标是促进车辆在交叉口的安全和有效移动。安全是通过及时分离冲突的移动来实现的,这里不再详细考虑。已经提出了各种措施,从不同角度量化交叉路口的效率:
Travel time. :在交通信号控制中,车辆的行驶时间被定义为一辆车进入交叉路口和离开交叉路口之间的时间差。最常见的目标之一是最小化车辆在网络中的平均行驶时间。
Queue length.:路网排队长度是路网中排队车辆的数量。
Number of stops.:车辆的停车次数是车辆经过的总次数。
Throughput.:吞吐量是指在一段时间内道路网络中完成行程的车辆数量。
2.3 Special Considerations
在实践中,应额外注意以下方面:
(1)设置黄色和全红色时间。黄色信号通常被设置为从绿色信号到红色信号的转换。在黄色之后,有一个全红色时段,在此期间,十字路口的所有信号都被设置为红色。黄色和全红色的时间可以持续3到6秒,允许车辆安全停车或通过十字路口,然后交通冲突的车辆才会得到绿色信号。
(2)设置最短绿灯时间。通常,需要最短的绿灯时间来确保在特定阶段行驶的行人能够安全通过交叉口。
(3)左转相位。通常,当左转相位高于某个阈值时,会添加左转相位。
3 METHODS IN TRANSPORTATION ENGINEERING
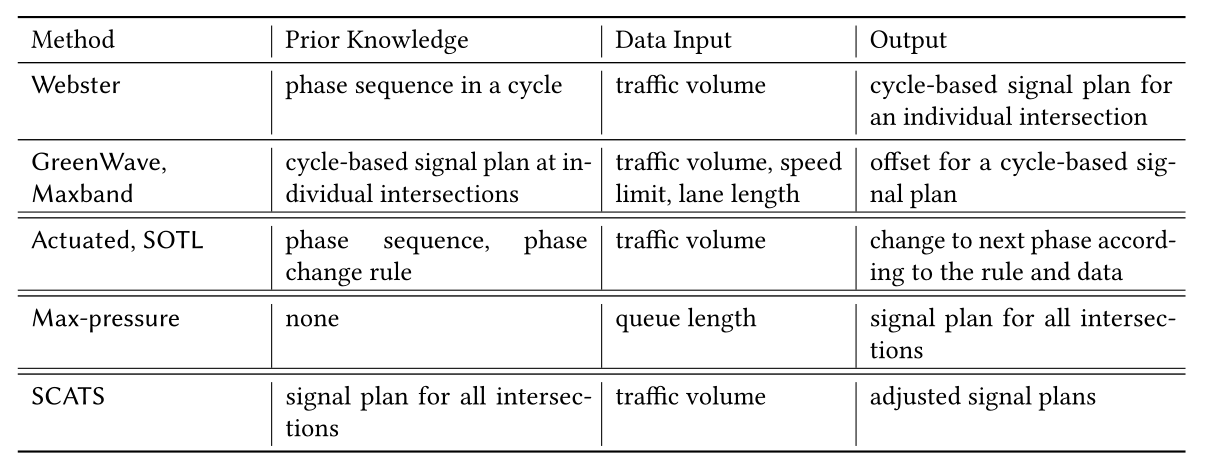
在本节中,我们将介绍运输领域中的几种经典方法,这些方法应作为基于RL的方法的比较基准。表1显示了涵盖方法的概述。关于交通方法的更全面的调查,我们请感兴趣的读者参考[马丁内斯等人,2011年;Roess等人,2004年]。
3.1 Webster (single intersection单交叉路口)
对于单个(孤立的)交叉口,交通工程中的交通信号计划通常由预先确定的周期长度、基于固定周期的相位序列和相位分割组成。韦伯斯特方法[Koonce等2008]是计算单个交叉口周期长度和相位分割的一种广泛使用的方法。假设在某个时间段(即过去5分钟或10分钟)内交通流量是均匀的,它有一个封闭形式的解,如公式所示。(1)和(2)为单个交叉路口生成最佳周期长度和相位分割,使所有车辆通过交叉路口的行驶时间最小化。
期望周期长度 \(C_{des}\)的计算基于Webster's Equation:
其中 \(N\) 是相数;\(t_L\) 是每个相位的总损失时间,可视为与全红色时间和车辆加速和减速相关的参数;参数 \(h\) 是饱和时间间隔(秒/车辆),这是连续车辆通过一个交叉路口的最小时间间隔;PHF(peak hour factor)是高峰时间因子的简称,这是一个衡量高峰时段交通需求波动的参数;并且参数v/c是期望的车辆与路口容量比,其表示在信号灯环境中十字路口有多繁忙。这些参数通常在不同的交通条件下有所不同,通常是根据经验观察和机构标准选择的。该方程表示 \(V_c\) 是一个函数,其中 \(V_c =\sum _{i}^{N}V^i_c\) 是所有关键车道交通量的总和,其指示在信号灯环境中十字路口有多繁忙,而 \(V^i_c\) 是第 \(i\) 相位关键车道交通量,其中关键车道是一个相位中交通流量与饱和流量之比最高的接近车道,通常由队列长度指示。
一旦决定了周期长度,绿色分割(即周期长度上的绿色时间)随后被计算为与每个阶段所服务的关键车道体积的比率成比例,如等式所示。(2):
其中,\(t_i\) 和 \(t_j\) 分别代表相位 \(i\) 和相位 \(j\) 持续时间。
公式(1)和(2)通常使用汇总数据来制定固定时间计划。然而,为了实时应用,也可以修改这些方程。例如,在交通均匀的情况下,可以证明韦伯斯特方法可以使所有车辆通过交叉口的行驶时间最小化或交叉口通行能力最大化。通过在短时间内收集数据,并假设在一个周期内交通需求没有波动,也没有冗余,即同时将 \(PHF\) 和 \(v/c\) 设置为 \(1\),等式。公式(2)可以重新组织为:
等式(3)的左边是用于交叉口交通运行的时间比例乘以车辆的饱和流量,即交叉口的通行能力。当容量等于流量需求时,周期长度 \(C_{des}\) 是严格满足流量需求的最小值。对于给定的交通需求,如果信号周期长度小于应用的 \(C_{des}\),队列长度将继续增加,并且交叉口变得过度饱和。如果应用的信号周期长度大于 \(C_{des}\),交叉口每辆车的平均延迟将随着周期长度线性增长。
3.2 GreenWave(绿流,某条道路上一路绿灯)
虽然韦伯斯特方法为单个交叉口生成信号计划,但相邻交通信号的信号时序之间的偏移(即相邻交叉口相位周期之间的起始时间)也应进行优化,因为信号通常非常接近。如果做不到这一点,可能会导致在一个信号上做出决定,从而恶化另一个信号上的交通运行。
GreenWave [Roess等人,2004]是运输领域实施协调的最经典的方法,其目的是优化偏移以减少沿某一方向行驶的车辆的停靠次数。给定单个交叉口的信号规划(即周期长度和相位分割),绿流要求所有交叉口共享相同的周期长度,这是单个交叉口给定周期长度的最大值。交叉点之间的偏移通过以下等式计算:
其中,\(L_{i,j}\)表示交叉口 \(i\) 和 \(j\) 之间的道路长度,\(v\) 表示车辆在道路上的预期行驶速度。
这种方法可以沿着指定的交通方向形成绿流,沿该方向行驶的车辆可以受益于绿色信号的渐进级联,而无需在任何交叉口停车。然而,绿流只针对单向流量进行优化。
3.3 Maxband
另一个典型的方法,Maxband [Little等人,1981],也将单个交叉口的信号计划作为输入,并优化相邻交通信号的偏移。与绿流不同,它旨在通过根据系统内各个交叉口的信号规划找到最大 bandwidth 来减少沿两个相反方向行驶的车辆的停靠次数。一个方向的 bandwidth 是绿流在一个周期长度内持续的时间的一部分。更大的 bandwidth 意味着一个方向上更多的流量可以不间断地通过信号。
和GreenWave一样,Maxband [Little等1981]要求所有交叉路口共享相同的周期长度,等于所有交叉路口周期长度的最大值。然后,Maxband制定一个混合整数线性规划模型,以生成一个对称的、统一宽度的带宽,受以下物理约束:
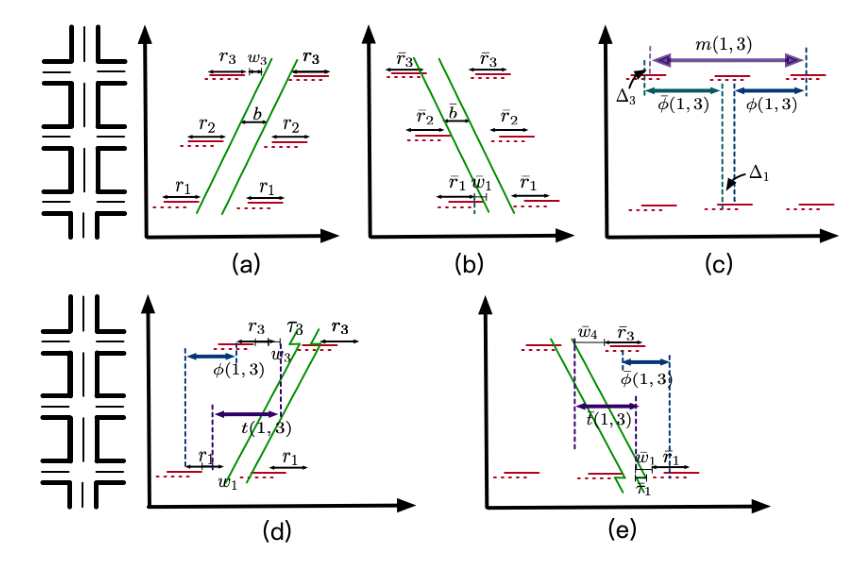
略
为了考虑各种新的方面,在原始方法的基础上引入了Maxband的许多重要扩展[Little等人,1981]。[Gartner等人1991]扩展到包括相反方向的不对称带宽、可变左转相位序列,以及关于周期时间长度和链接特定进度速度的决策。[Stamatiadis和Gartner 1996]提出了新的多波段、多权重方法,它还结合了所有以前的决策能力。
3.4 Actuated Control
启动控制测量来自当前相位和其他冲突相位的绿色信号的“请求”,然后基于一些规则来决定是保持还是改变当前相位。当前阶段和其他冲突相位的“请求”定义如下:
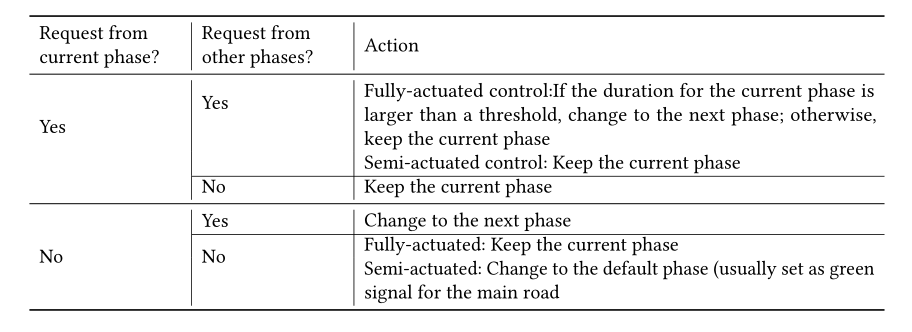
当当前相位的持续时间没有达到最小时间段,或者当前相位的进入车道上有车辆并且在交叉口附近的距离内时,产生当前相位的延长绿色信号时间的请求。简而言之,我们称之为“接近绿色信号”。
当冲突相位中等待车辆的数量大于阈值时,产生对绿色信号的竞争相位的请求。
根据规则的不同,有两种驱动控制:全驱动控制和半驱动控制。表2列出了决定保持或改变当前相位的规则。
3.5 Self-organizing Traffic Light Control

自组织交通灯控制(SOTL)基本上与具有额外需求响应规则的全驱动控制相同[Cools等人,2013;Gershenson 2004]。SOTL和全驱动控制的主要区别在于对当前相位请求的定义(尽管它们都要求最小的绿色相位持续时间):在全驱动控制中,只要有车辆接近绿色信号,就会产生当前相位的请求,而在SOTL,除非接近绿色信号的车辆数量大于阈值(不一定是1),否则不会产生请求。具体来说,SOTL控制的规则如表3所示。
3.6 Max-pressure
最大压力控制[Varaiya 2013]旨在通过最小化交叉口相位的“压力”来平衡相邻交叉口之间的队列长度,从而降低过度饱和的风险。压力的概念如图5所示。形式上,运动信号的压力可以定义为(交通运动的)进入车道上的车辆数量减去相应的离开车道上的车辆数量;相位的压力被定义为进路和出路的总队列长度之间的差异。通过将单个交叉口的相位压力设置为最小,证明了最大压力可以使整个路网的通行能力最大化。对证明感兴趣的读者,请参考[Varaiya 2013]。
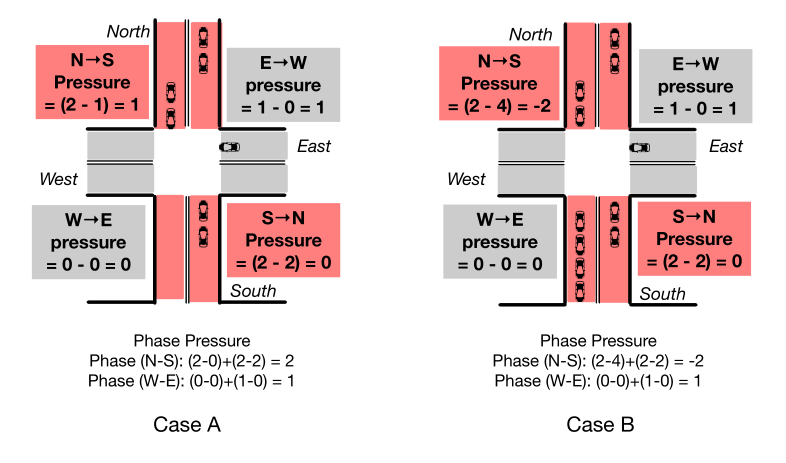
图5 Case A中 $N \rightarrow S $ 图片中应该是错了,应为\(Pressure=(2-0)=0\)
[Varaiya 2013]中提出的最大压力控制在算法1中正式总结。从第3行到第7行,该方法选择压力最大的相位,将其激活为下一相位,并在给定的时间段 \(t_{min}\) 内保持所选相位。

3.7 SCATS
悉尼协调自适应交通系统采用预定义的信号计划(即周期长度、相位分割和偏移)作为输入,并根据预定义的性能测量从这些交通信号中反复选择。它的测量,如饱和度,详细如下:
其中,\(g\) 是可用的绿色信号时间(以秒为单位),\(gE\) 是车辆通过交叉口的有效绿色时间,等于可用的绿色信号时间减去浪费的绿色时间;并且通过检测来计算浪费的绿色时间 \(-h’\) 是检测到的总时间间隙, \(n\) 是检测到的车辆数量,\(h\) 是车辆之间的单位饱和间隔(秒), 它代表连续车辆经过一个点之间的最小时间间隔,通常由专家知识设定。
相位分割(即所有相位的相位时间比)、周期长度和偏移是使用类似的机制从几个预定义的计划中选择的。以相位分割的选择机制为例。如算法2所示,该算法首先使用等式(10)为当前信号计划计算 \(DS\)。在每个周期结束时(第2行到第4行)。然后,从第6行到第10行,该算法使用以下等式推断当前周期中未应用的其他信号计划的DS:
其中,\(DS_p\) 和 \(g_p\) 为当前信号计划中相位p的饱和度和绿色信号时间,而дj为信号计划j中相位p的饱和度。然后,算法选择具有最佳DS的信号计划。

4 REINFORCEMENT LEARNING BASED TRAFFIC SIGNAL CONTROL
最近,人们提出了不同的人工智能技术来控制交通信号,如模糊逻辑算法[Gokulan和Srinivasan 2010],群体智能[Teodorovi 2008],强化学习[ElTantawy和Abdulhai 2012Kuyer等人,2008年;曼尼恩等人,2016年;Wiering 2000]。在这些技术中,RL近年来更具趋势。
4.1 Preliminaries
4.1.1 Basic concepts.
为了使用RL解决交通信号控制问题,我们首先在问题1中介绍RL的公式,然后介绍交通信号控制如何适合RL设置。我们还将在交通信号控制的背景下介绍多智能体RL(MARL)的制定。
Problem 1 (RL Framework).
通常情况下,单智能体RL问题被建模为马尔可夫决策过程(MDP) \(< S,A,P,R,γ>\),其中\(S,A,P,R,γ\)分别是状态表示集,动作集,概率状态转移函数,奖励函数和折扣因子。给定两个集合 \(X\) 和 \(Y\) ,我们用 \(X × Y\) 来表示 \(X\) 和 \(Y\) 的笛卡尔积,即\(X × Y = \{(x,y)|x ∈ X,y ∈ Y\}\)。定义如下:
-
\(S\) : 在第 \(t\) 步,智能体观察状态 \(s^t∈ S\)。
-
\(A,P\) : 在第 \(t\) 步,智能体在 \(a^t ∈ A\) 集合中选取动作,这根据状态转移函数在环境中进行状态转换。
\[P(st+1|st,at) : S × A → S \tag{12} \] -
\(R\) : 在第 \(t\) 步,智能体通过奖励函数获得奖励。
\[R(s^t,a^t):S×A\rightarrow \mathbb R \tag {13} \] -
\(γ\) : 智能体的目标是找到一种策略,使回报最大化,预期回报是奖励的折扣总和:
\[G^t:=\sum_{i=0}^{\infty} \gamma^ir^{t+i} \tag {14} \]其中折扣因子 \(γ ∈ [0,1]\) 控制着当前回报相对于未来回报的重要性(控制着即刻回报与未来回报谁的收益高,也就是智能体更加注重即刻收益,还是未来收益)。在这里,我们只考虑持续的智能体-环境交集,它不以终端状态结束,而是无限制地持续下去。
Definition 4.1 (Optimal policy and optimal value functions).
解决强化学习任务,粗略的说就是找到一个最大化期望收益的最优策略 \(π^*\)。虽然智能体只获得关于其即时的、一步动作表现的回报,但是找到最优策略 \(π^*\) 的一种方法是遵循最优的动作价值函数或最优状态价值函数。策略 \(π\) 的动作价值函数(Q函数),\(Q^ π: S × A → \mathbb R\),是状态-动作对的期望回报 \(Q^π(s,a) = \mathbb E_π[G^t|s^t= s,a^t= a]\).
最优的 Q-function 定义为\(Q^*(s,a) = max_πQ^π(s,a)\)。它满足Bellman optimality equation:
策略 \(\pi\) 的状态值函数,\(V^π: S → \mathbb R\),是一个状态的预期回报 \(V^π(s) = \mathbb E_π[G^t|s^t= s]\)。最优状态值函数定义为 \(V^*(s)= max_πV^π(s)\)。它满足Bellman optimality equation:
Example 4.2 (Isolated Traffic Signal Control Problem).
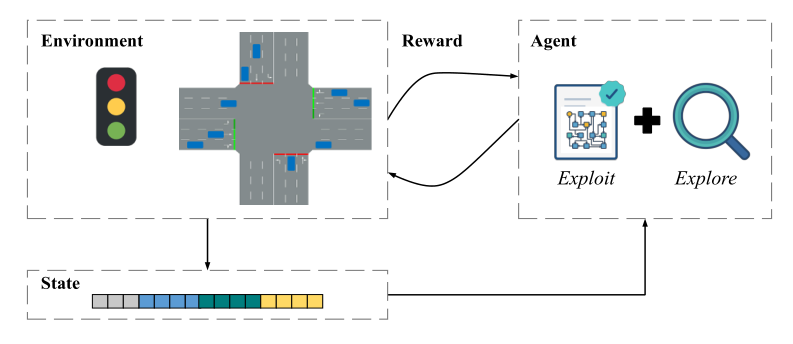
图6说明了交通灯控制问题中RL框架的基本思想。 环境就是道路上的交通状况,智能体 G 控制交通信号。在每个时刻 \(t\) ,将生成环境描述(例如,信号相位、车辆等待时间、车辆队列长度和车辆位置)作为状态 \(s_t\)。智能体将预测下一步要采取的动作,以最大化由等式(14)定义的预期回报。其中动作可以将单个交叉路口中信号相位改变到某个特定信号相位。动作 \(a^t\) 将在环境中执行,并产生一个奖励 \(r^t\),其中奖励可以根据交叉口的交通状况来定义。通常,在决策过程中,智能体采取的策略结合了学习策略的开发(利用已知策略找最优)和对新策略的探索(在已知策略上再去找新的策略)。
Problem 2 (Multiagent RL Framework).
MDP对多智能体情况的概括是随机博弈(SG)。随机博弈定义为一个元组 \(\Gamma= < \bf S, P, A, R, O ,N,γ>\),其中\(\bf S, P,A, R, O,N,γ\)分别代表状态集(states),转移概率函数(transition probability functions),动作(joint actions),奖励函数(reward functions),单独的观测值(private observations,),智能体数量(number of agents ),折扣因子(discount factor respectively)。定义如下:
-
$\bf N $: \(N\) 个智能体被定义为 \(i ∈ I = \{1, . . .N\}\).
-
\(\bf S, O\): 在每个时刻 \(t\), 代理 \(i\) 根据观测函数 \(\bf S× I \rightarrow O\) 描绘真实环境状态 \(s^t∈ S\) 相关的观测值 \(o^t_i \in O\) .
-
$ \bf P,A$ :智能体 \(i\) 的动作 \(A_i\) 被定义为一组相位。在时刻 \(t\),每个智能体采取一个动作 \(a^t_i \in A_i\),形成一系列动作(轨迹)\(a^t=a_1,...,a_N\),在环境中根据状态转移函数,这样就引起了状态的转变。
\[P(s^{t+1}|s^t,a^t) : S × A_1× · · · × A_N→ Ω( S) \tag {17} \]其中 \(Ω( S)\) 表示状态分布空间。
-
\(\bf R\):在随机博弈环境中,一个智能体获得的报酬也受到其他智能体行为的影响。因此,在时刻 \(t\),每个智能体 \(i\) 通过一个奖励函数获得奖励 \(r^t_i\)
\[R_i(s^t, a^t) : S × A_1× · · · × A_N→ \mathbb R \tag{18} \] -
\(γ\) :直觉上,一系列行动对环境有长期影响。每个智能体 \(i\) 选择的动作 action 遵循某个策略 \(π_i\) ,目标是回报最大化 \(G^t:=\sum_{j=0}^{\infty} γ^jr^{t+j}_i\) ,其中折扣因子 \(γ ∈ [0,1]\) 控制即刻收益相对于未来收益的重要性。
Example 4.3 (Multi-intersection Traffic Signal Control Problem).
对于具有多个交叉路口的网络,智能体被定义为环境中第 \(N\) 个交叉口的信号控制器。用RL控制的交通信号智能体的目标是学习每个智能体的最优策略以及优化整个环境的交通状况。在每一个时刻 \(t\) ,每个智能体 \(i\) 观察环境的一部分作为观察值 \(o^t_i\) 。智能体预测下一步要采取的动作 \(a^t\)。在现实世界中, \(A_i\)大多是提前定义好的,即交通信号只能在几个相位之间变化。动作会在环境中被执行,并产生奖励,其中奖励可以在环境中的单个交叉点或一组交叉点上定义。
4.1.2 Basic components of RL for traffic signal control.
在RL框架下,有四个主要组成部分来阐述问题:
- **Reward design. **:当智能体学习最大化数字奖励时,奖励的选择决定了学习的方向。
- **State design. **:状态描述了路口的情况,并将其转化为价值。因此,状态的设计应该充分描述环境。
- Selection of action scheme. :不同的行动方案对交通信号控制策略的性能也有影响。比如,如果智能体的动作被定义为“从某个相位改变到某个相位”, 交通信号将具有比将动作定义为“保持当前相位或在这个周期中改变到下一个相位”更灵活的相位序列。
- Coordination strategy. :如何实现协调是使信号控制问题复杂化的挑战之一。在城市环境中,信号通常非常接近,车辆离开一个信号灯会影响车辆到达下一个下游交叉口的模式。因此,必须联合优化相邻交通信号的信号时序。
4.2 RL Formulation
RL的一个关键问题是如何制定RL中变量的设置,即奖励、状态和动作定义。在最近的研究中[van der Pol 2016;魏等2018;Wiering 2000],交通信号控制的典型奖励定义是队列长度、等待时间和延迟等几个分量的加权线性组合。状态特征包括诸如队列长度、汽车数量、等待时间和当前交通信号相位等组成部分。近期作品中【范德波尔2016;魏等人,2018年],车辆在道路上的位置的图像也被考虑在状态中,并被反馈到深度神经网络以学习控制策略。关于奖励、状态和行为的更多讨论,我们请感兴趣的读者参考[El-Tantawy和Abdulhai 2011曼尼恩等人,2016年;Yau等人,2017年]。
4.2.1 State Definitions.
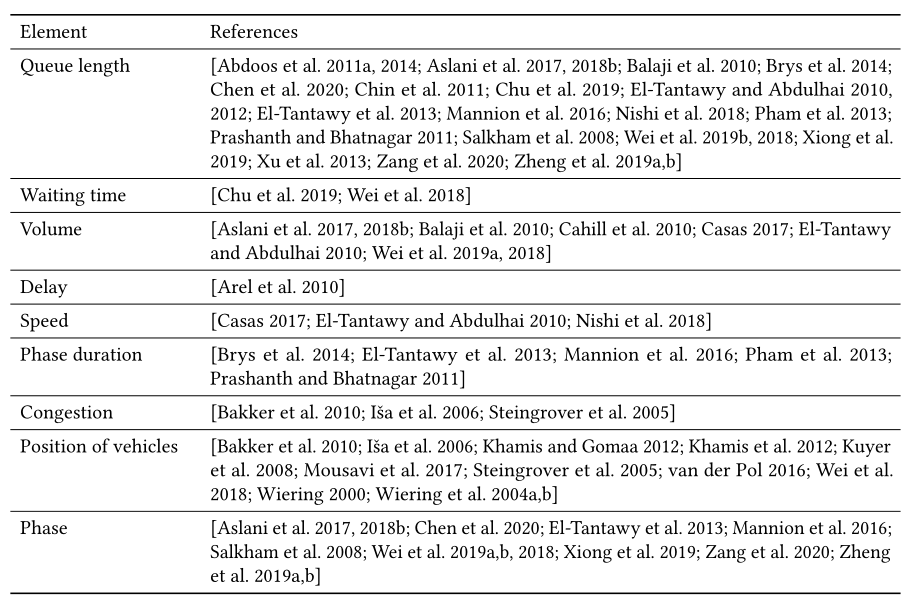
在每个时刻,智能体接收一些环境的定量描述作为状态表示。如表4所示,已经提出了各种元素来描述交通信号控制问题中的环境状态:
- **Queue length. ** :车道的排队长度是车道上等待车辆的总数。车辆的“等待”状态有不同的定义。在[Wei等2018]中,将速度小于0.1 m/s的车辆视为等待;[Bakker等人,2005年;Kuyer等人,2008年],就位置而言没有运动的车辆被认为是等待。
- Waiting time. :车辆的等待时间被定义为车辆处于“等待”状态的时间段(参见上面的队列长度了解“等待”的定义)。等待期开始时间的定义可能不同:在[van der Pol 2016;Wei等人,2018年],他们考虑从车辆移动的最后时间戳开始的等待时间,而[Brys等人,2014年;Pham等人,2013年;Wiering 2000]考虑从车辆进入路网开始的等待时间。
- **Volume. ** :车道的体积被定义为车道上的车辆数量,等于车道上排队车辆和行驶车辆的总和。
- **Delay. ** :车辆延误定义为车辆在环境中行驶的时间减去预期行驶时间(等于距离除以速度限制)。
- **Speed. ** :车辆速度用于测量车辆行驶的速度,这在很大程度上受预定义速度限制的影响。大多数文献使用速度分数,该分数是通过车速除以速度限制来计算的。
- Phase duration. :当前相位的相位持续时间定义为当前相位已经持续了多久了。
- Congestion. :一些研究考虑了输出方法的拥塞,以便在拥塞和不拥塞的情况下进行有效的学习。车道的拥堵可以定义为一个指标(0表示无拥堵,1表示拥堵),也可以定义为拥堵水平,即车辆数量除以车道上允许的最大车辆数。
- Positions of vehicles. :车辆的位置通常被集成为一个图像表示,该图像表示被定义为车辆位置的矩阵,其中“1”表示某个位置上有车辆,而“0”表示该位置上没有车辆[穆萨维等人,2017年;van der Pol 2016魏等2018]。
- Phase. :相位信息通常通过预定义信号相位组中当前相位的索引集成到状态中[El-Tantawy等人,2013;van der Pol 2016魏等2018]。
这些元素在状态表示中也有一些变体。这些元素可以在车辆层面上定义为车辆位置的图像表示[van der Pol 2016;魏等人,2018年]),通过对相应车道上的所有车辆求和或求平均值,在车道水平上进行计算[魏等人,2018年]。
最近,有一种趋势是在基于 RL 的交通信号控制算法中使用更复杂的状态,希望获得对交通状况的更全面的描述。具体来说,最近的研究建议使用图像[穆萨维等人,2017年;van der Pol 2016魏等2018]来表示状态,这导致了具有数千或更多维度的状态表示。然而,以如此高的状态维数进行学习通常需要大量的训练样本,这意味着训练RL智能体需要很长时间。更重要的是,更长的学习时间表不一定会带来显著的性能提升,因为智能体可能更难从状态表示中提取有用的信息。
4.2.2 Reward Functions.
奖励定义了强化学习问题的目标。等效地,我们可以将 RL 看作是一种朝着目标优化的方法,并且该目标被指定为 RL 环境中的奖励函数。在每个决策点,智能体对环境采取动作,环境向智能体发送一个称为奖励的数字值。智能体的目标是长期获得最大的总回报。
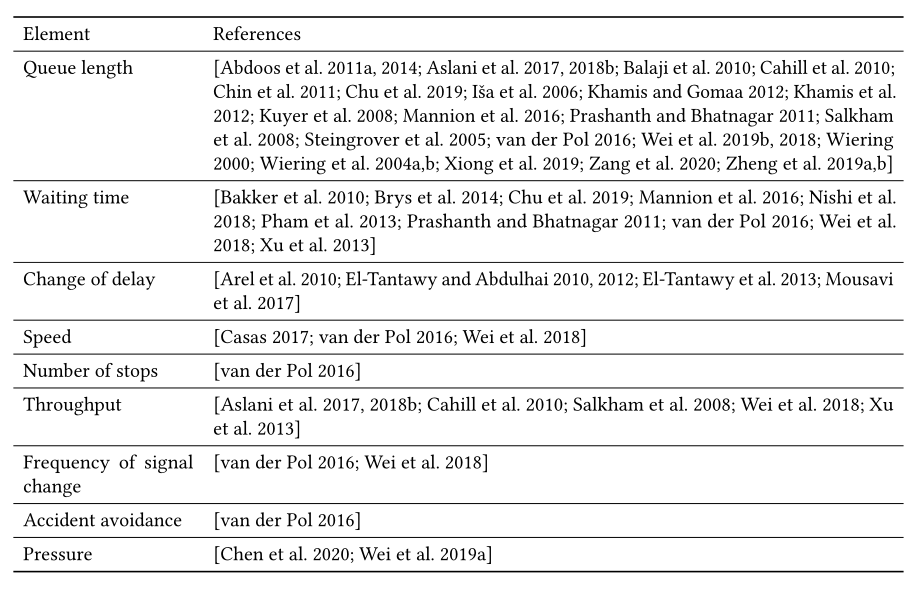
在交通信号控制问题中,虽然最终目标是最小化所有车辆的行驶时间,但行驶时间很难在RL中作为有效的奖励,原因有几个。首先,车辆的行驶时间不仅受交通信号的影响,还受其他因素的影响,如车辆的自由流动速度。第二,当交通信号控制器事先不知道车辆的目的地时(现实世界中经常是这种情况),优化网络中所有车辆的行驶时间变得特别困难。在这种情况下,当网络中的多个交叉口已经采取了多个动作时,车辆的行驶时间只能在它完成其行程之后进行测量。因此,奖励函数通常被定义为表5中因素的加权和,这些因素可以在执行动作后有效地测量:
- **Queue length. ** :排队长度定义为所有接近车道的排队长度 \(L\) 之和,其中 \(L\) 计算为给定车道上等待车辆的总数。类似于第4.2.1节中队列长度的定义,车辆的“等待”状态有不同的定义。最小化队列长度相当于最小化总交通时间。
- Waiting time. :车辆的等待时间被定义为车辆已经等待的时间。类似于4.2.1节中等待时间的定义,对于如何计算车辆的等待时间有不同的定义。典型的奖励函数考虑车辆经历的等待时间的负值。
- **Change of delay. ** :总累积延迟的变化(节省)是两个连续决策点的总累积延迟之差。总累积延迟时间 \(t\) 是系统中当前所有车辆截至时间 \(t\) 的累积延迟总和。
- **Speed. ** :典型的奖励是道路网络中所有车辆的平均速度。道路网络中车辆的平均速度越高,表示车辆到达目的地的速度越快。
- Number of stops. :奖励可以使用网络中所有车辆的平均停靠次数。理论上,停靠次数越少,交通越顺畅。
- Throughput. :吞吐量被定义为在最后一次动作后的某个时间间隔内通过交叉口或离开网络的车辆总数。最大化吞吐量也有助于最小化所有车辆的总行驶时间,尤其是在道路网络拥堵的情况下。
- Frequency of signal change. :信号变化的频率被定义为信号在特定时间段内变化的次数。直觉上,学习的策略不应导致闪烁,即频繁改变交通信号,因为车辆通过交叉口的有效绿灯时间可能会减少。
- **Accident avoidance. ** :还有一些研究对避免事故有特殊的考虑。比如紧急停车应该不多。此外,应该防止堵塞或潜在的碰撞。
- **Pressure of the intersection. ** :在 [Wei et al. 2019a] 中 ,交叉口的压力被定义为每次交通运动的绝对压力之和。直观地说,较高的压力表明进入通道和离开通道之间的不平衡程度较高。
这些因素也有一些变体来衡量行动后的即时回报。奖励可以被定义为在特定决策点的因子的值,或者被定义为在特定时期内相应的总累积值之间的差值。由于这些因素大多是一系列行动的结果,而一个行动的效果很难得到反映,因此是否将这些因素作为原始值或作为它们的差异仍有待讨论。
虽然将奖励定义为几个因素的加权线性组合是现有研究中的常见做法,但在交通信号控制环境中,这些特殊设计存在两个令人担忧的问题。首先,不能保证最大化所提出的奖励等同于优化交通时间,因为它们在交通理论中没有直接联系。其次,调整每个奖励函数组件的权重相当棘手,权重设置的微小差异可能会导致截然不同的结果。虽然表5中提到的因素都与交通时间相关,但它们的不同加权组合产生非常不同的结果。不幸的是,目前还没有选择这些权重的原则性方法。
4.2.3 Action Definitions.
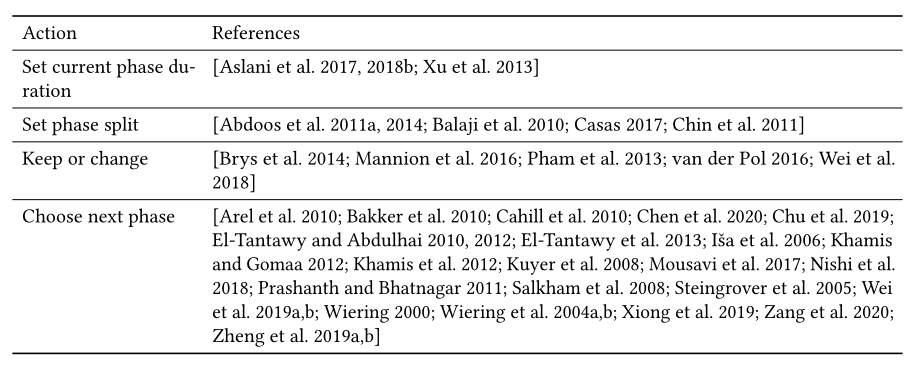
现在主要有四种类型的操作,如表6所示:
- 设置当前相位持续时间。在这里,智能体通过从预定义的候选时间段中进行选择来学习设置当前阶段的持续时间。
- 设置基于周期的相位比。这里,动作被定义为信号将为下一个周期设置的相位分割比例。通常给出总周期长度,预定义候选相位分割比例。
- 在基于周期的相序中保持或改变当前相位。在这里,一个动作被表示为一个二进制数,这表示智能体决定保持当前阶段或改变到下一个阶段。
- 选择下一相位。决定在可变相序中改变到哪个相位,其中相序不是预先确定的。这里,动作是接下来应该采取的相位索引。因此,这种信号定时更加灵活,智能体正在学习选择要改变的相位,而不需要假设信号会周期性地改变。
4.3 Learning Approaches
从不同的角度来看,RL方法有不同的算法框架。根据是否学习状态转移函数,RL方法可以分为基于模型(model-based)的方法和无模型(model-free)的方法。
根据是学习值函数(value function)还是策略参数(policy parameter),RL 方法可以分别分为基于值(value-based)的方法或策略梯度(policy-gradient)方法(这两种方法的组合是actor-critic方法)。根据函数、策略和模型是通过每个状态(或state-action对)的表来学习,还是通过参数化的函数表示来学习,RL方法又可以分为表格方法或近似方法。

4.3.1 Model-based vs. model-free methods.
根据RL的建模,[Arulkumaran等2017;卡尔布林等人[1996]将当前的RL方法分为两类:基于模型的方法(model-based)和无模型(model-free)方法。对于一个状态和动作空间都很大的问题,通常很难进行百万次实验来覆盖所有可能的情况。基于模型的方法试图对状态之间的转移概率进行显式建模(即,学习等式(12)或(17)),这可以用于更有效地对环境进行采样(智能体可以根据该转移概率获取数据样本)。具体来说,给定这个模型,我们将知道每个动作将把代理带到哪个状态。相比之下,无模型方法直接估计状态-动作对的回报,并基于此选择动作。因此,即使转移概率难以建模,也可以使用无模型方法。
在交通信号控制的背景下,为了开发基于模型的模型,需要知道或模拟环境的转移概率,如所有车辆的位置、速度和加速度,以及所有交通信号的操作。但是,既然人的驾驶行为不同,很难预测。目前,大多数基于RL的交通信号控制方法都是无模型(model-free)方法,如表7所示。
4.3.2 Value-based, policy-based vs. actor-critic methods.
根据评估潜在奖励和选择动作的不同方式,强化学习方法可分为以下三类,如表8所示:
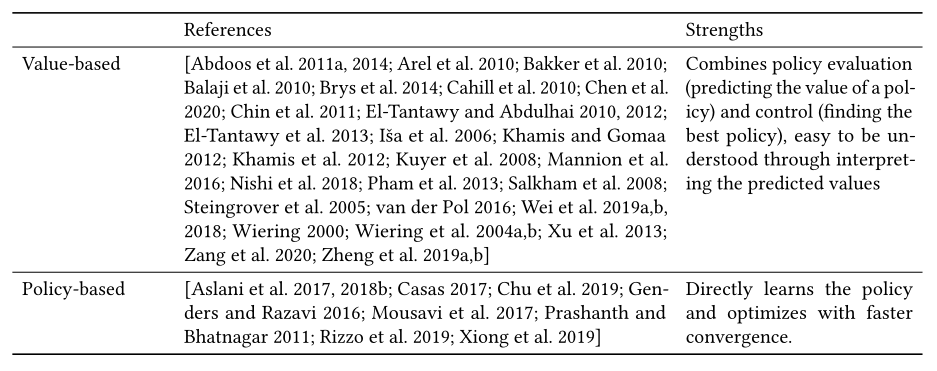
基于值(value-based)的方法近似于状态-价值函数( state-value function )或状态-动作 价值函数(state-action value function )(即每个状态或状态-动作对的回报),策略是从学习的价值函数隐式获得的(有了价值函数,然后根据价值函数推断出来的策略函数)。基于价值的方法,包括Q-learning [Abdoos et al. 2011b; Chin et al. 2011]和DQN [van der Pol 2016; Wei et al. 2018],直接对状态值或状态动作值进行建模(例如,在当前交通状况下,如果进行一个动作,平均速度增加/减少多少将生效)。这样,状态和奖励就可以直接馈入模型,无需额外处理。然而,这些方法通常与ϵ-greedy动作选择方法相结合,因此当ϵ最终衰减到一个较小的数字时(即,在某些状态下进行哪个动作是确定性的),将导致几乎确定性的策略。这可能会导致代理陷入一些看不见或表现不佳的情况,而没有改善。此外,这些方法只能处理离散的动作,因为每个动作都需要单独的建模过程。
基于策略的方法直接沿着方向更新策略(例如,在特定状态下进行动作的概率)参数,以最大化预定义的目标(例如,平均预期奖励)。基于策略的方法,尝试学习某个状态下不同动作的概率分布。基于策略的方法的优势在于它不要求操作是离散的。此外,它可以学习随机策略,并不断探索潜在的更有回报的行动。Actor-Critic是基于策略的方法中广泛使用的方法之一。它在学习行动概率分布的策略时包含了基于价值的思想,Actor控制我们的智能体的行为(基于策略),而Critic衡量所进行的动作有多好(基于价值)。交通信号控制中的Actor-Critic方法 [Aslani et al. 2018a, 2017; Mousavi et al. 2017; Prashanth and Bhatnagar 2011]利用了价值函数逼近和策略优化的优势,在交通信号控制问题上表现出优异的性能。
4.3.3 Tabular methods and approximation methods.
对于小规模离散强化学习问题,其中state-action对可以被枚举,通常的做法是使用表来记录价值函数、策略或模型。然而,对于一个大规模或连续的问题(状态或动作是连续的),枚举所有的state-action对是不现实的。在这种情况下,我们需要使用状态和动作的近似函数来估计价值函数、策略或模型。
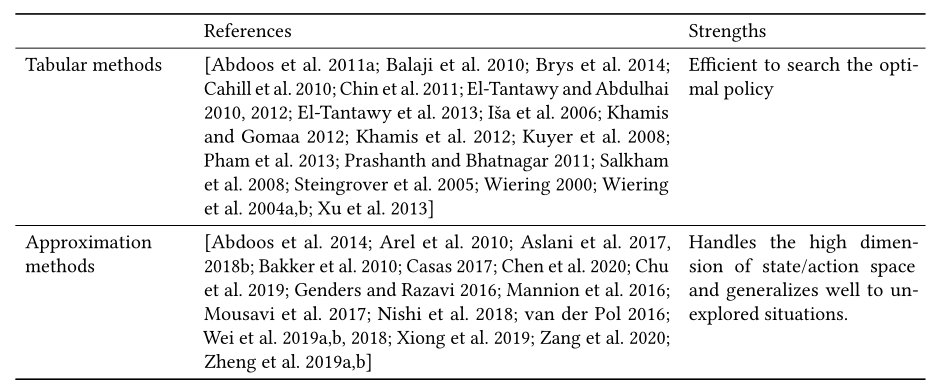
在信号控制的问题场景中,早期的方法使用简单的状态特征,如拥挤水平(可转换为离散状态值),并采用表格Q学习[Abdulhai et al. 2003; El-Tantawy and Abdulhai 2010]学习价值函数。因此,对于交通信号控制中的复杂场景,这些方法不能扩展到大的状态空间。此外,表格方法将具有相似特征的样本视为两种完全不同的状态,这将降低在训练中利用样本的效率。为了解决这些问题,最近的研究提出使用连续状态表示的近似[Abdoos et al. 2014; Arel et al. 2010; Arulkumaran et al. 2017; Bazzan and Klügl 2014; Brys et al. 2014; El-Tantawy and Abdulhai 2012; El-Tantawy et al. 2013; Khamis and Gomaa 2012; Mannion et al. 2016; van der Pol 2016; Wei et al. 2018]。函数逼近可以通过多种机器学习技术来实现,如tile coding [Albus 1971]或深度神经网络。这些方法可以更有效地利用具有相似状态值的样本,并处理具有连续范围的更多信息特征,例如车辆的位置。表9总结了基于RL的交通信号控制方法在表格或近似方面的分类。
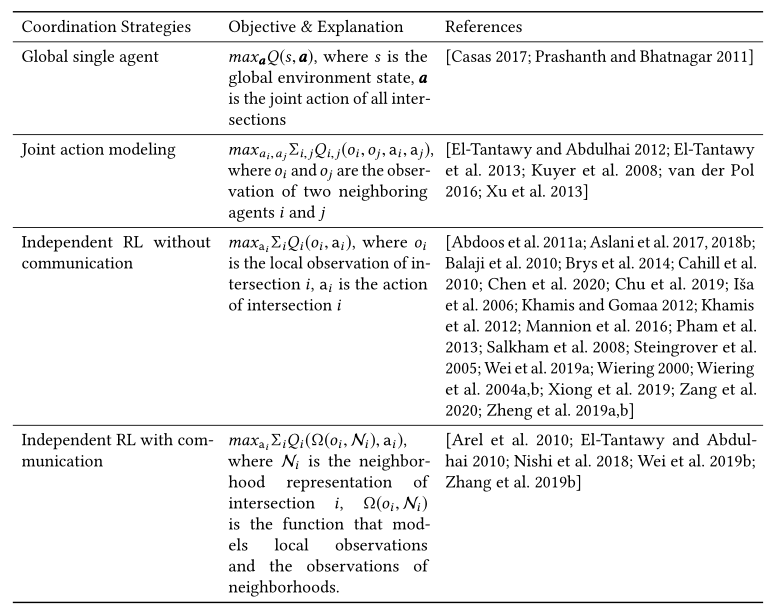
4.4 Coordination Strategies
协调多交叉口场景有利于信号控制。由于RL的最新进展提高了隔离交通信号控制的性能 [van der Pol 2016; Wei et al. 2018],已经努力设计与MARL代理商合作的策略。Liturature[Claus and Boutilier 1998]将MARL分为两类:联合行动学习者和独立学习者。如表10所示,我们将这种分类扩展到交通信号控制问题。
- Global single agent. :一个简单的解决方案是使用一个中央智能体来控制所有的交叉口。它直接以状态为输入,同时学习设置所有路口的联合动作。然而,这种方法可能导致维数灾难,它包括状态-动作空间在状态和动作维数上的指数增长。
- Joint action modeling. : [Kuyer et al. 2008]和[van der Pol 2016] 考虑使用协调图的学习智能体之间的显式协调机制,使用max-plus算法扩展[Wiering 2000]。它们将全局Q函数分解为局部子问题的线性组合。\(\hat Q (o_1,...o_N,a)=\sum_{i,j}Q_{i,j}(o_i,o_j,a_i,a_j)\)其中 \(i\) 和 \(j\) 对应于相邻智能体的索引。
- Independent RL. :还有一系列研究使用单个RL智能体来控制多交叉口网络中的交通信号[Abdoos et al. 2011a; Balaji et al. 2010; Brys et al. 2014; Cahill et al. 2010; El-Tantawy and Abdulhai 2010; Mannion et al. 2016; Pham et al. 2013; Salkham et al. 2008]。在这些方法中,每个交叉点由一个RL智能体控制,该智能体感知环境的一部分,并相应地适应(或反应)环境,最终形成几个同步子结构。
- Without communication. :这些方法不使用显式通信来解决冲突。取而代之的是,对智能体 \(i\) 的观察是基于交叉口 \(i\) 的局部交通状况来定义的。在一些简单的场景中,如主干网,这种方法在形成几个小绿流(一路绿灯)时表现良好。然而,当环境变得复杂时,来自邻近智能体的非平稳影响将被带入环境,并且如果智能体之间没有通信或协调机制,学习过程通常不能收敛到平稳策略 [Nowe et al. 2012]。在高度动态的环境中,在环境再次发生变化之前,智能体可能没有时间感知和适应变化。
- With communication. :虽然在多代理系统中使用单个RL来控制每个代理可以在简单的环境下形成协调,但是代理之间的通信可以使代理作为一个组来工作,而不是在环境是动态的并且每个代理的能力和对世界的可见性有限的复杂任务中的个体集合[Sukhbaatar et al. 2016]。这对于现实世界中的交通信号控制尤其重要,在现实世界中,交叉口非常接近,并且交通是高度动态的。一些研究还将邻居的交通状况直接添加到 \(o_i\) 中,[Nishi et al. 2018; Wei et al. 2019b]提出使用图卷积网络[Schlichtkrull et al. 2018]其中协作智能体学习在他们之间进行通信。该方法不仅学习了相邻智能体的隐藏状态与目标智能体之间的相互作用,还学习了交叉口之间的多次接力的影响。
4.5 Experimental Settings
在本节中,我们将介绍一些影响交通信号控制策略性能的实验设置:模拟环境、道路网络设置和交通流设置。
-
Simulation environment. :部署和测试交通信号控制策略涉及高成本和高劳动强度。因此,在实际实施之前,模拟是一种有用的替代方法。交通信号控制的模拟通常涉及大型和异构场景,这些场景应该考虑车辆环境中的一些特定移动模型,包括车辆跟随、车道变换和路线选择。由于移动性模型会显著影响模拟结果,模拟模型必须尽可能接近现实。
-
Road network. :在当前文献中探索了不同种类的道路网络,包括合成的和真实世界的道路网络。虽然大多数研究在合成网格网络上进行实验,但与城市规模相比,网络规模仍然相对较小。
-
**Traffic flow. ** :仿真中的流量也会影响控制策略的性能。通常,流量越动态、越大,RL方法就越难学习到最优策略。
4.5.1 Simulation environment.
各种公共可用的交通模拟器目前正由研究团体使用。在本节中,我们简要介绍了当前交通信号控制文献中使用的一些开源工具。具体来说,由于基于RL的方法需要详细的状态表示,如车辆级别的信息,大多数文献依赖于微观模拟,在微观模拟中,各个车辆的运动通过微观属性来表示,例如每个车辆的位置和速度。其他专有模拟器,如 Paramicsor 或 Aimsun ,这里就不介绍了。关于开源模拟器的详细比较,请参考 [Martinez et al. 2011]。
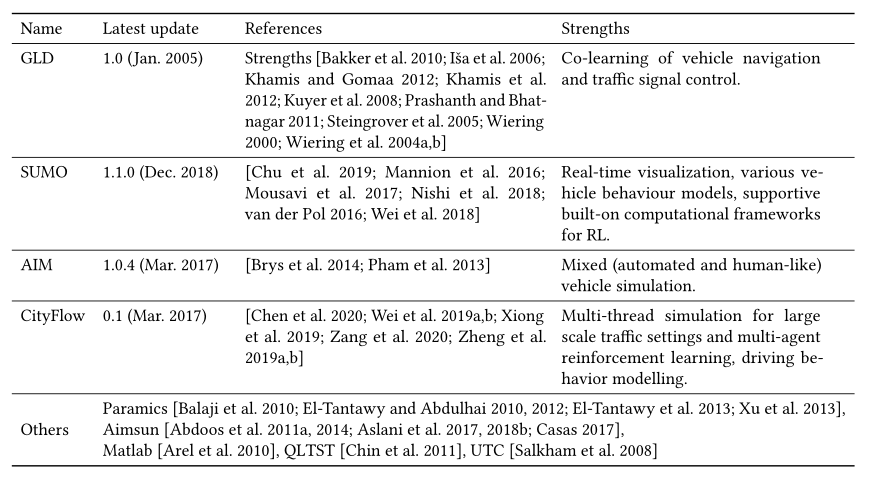
- The Green Light District (GLD)3 :GLD是一个开源的交通流模拟器,可以用来评估人工智能交通灯控制器算法和汽车协同学习导航算法的性能。车辆在边缘节点(即不与交叉口相连的道路的一端)进入网络,每个边缘节点在每个时间步长(生成率)都有一定的概率产生车辆。每个生成的车辆被分配给其他边缘节点之一作为目的地。可以调整每个边缘节点的目的地分布。根据速度、长度和乘客数量,可以有几种类型的车辆。
- The Autonomous Intersection Management (AIM) :AIM是一个微观交通模拟器,它主要支持由许多交叉口连接的南北和东西多车道道路的曼哈顿拓扑结构。由奥斯汀得克萨斯大学学习智能体研究小组开发的AIM支持车辆导航、加速和减速,以及微妙的细节,包括可变的车辆尺寸。
- Simulation of Urban MObility (SUMO) :SUMO是一个开源的交通模拟程序,主要由位于德国航天中心的交通系统研究所开发。在其他功能中,它允许存在不同类型的车辆、具有多条车道的道路、交通灯、查看网络和模拟实体的图形界面,以及称为TraCI的API在运行时与其他应用程序的互操作性。此外,该工具可以通过允许没有图形界面的版本来加速。此外,它将能够从OpenStreetMap导入现实世界的道路网络,车辆可以从网络中的任何位置进入系统。SUMO还支持其他高级计算框架,用于深度RL和交通微观模拟的控制实验。
- CityFlow. :CityFlow [Zhang et al. 2019a] 是一个适用于大规模城市交通场景的多智能体强化学习环境。它支持道路网络和交通流的真实世界定义,并能够对全市交通设置进行多线程模拟。它还提供了用于强化学习的应用编程接口,适用于交通信号控制和驾驶行为建模等任务。
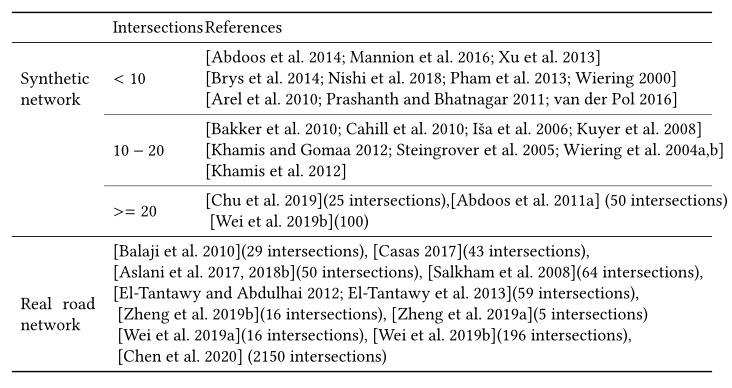
4.5.2 Road network.
粗略地说,道路网络是一个有向图,其节点和边分别代表交叉点和道路。具体而言,现实世界的道路网络在道路属性(如每个车道的位置、形状和速度限制)、交叉口、交通运动、交通信号逻辑(运动信号相位)方面可能比合成网络更复杂。表12总结了文献中的道路网络。虽然现有的研究对不同类型的道路网络进行了实验,但测试网络中的交叉口数量大多小于20个。
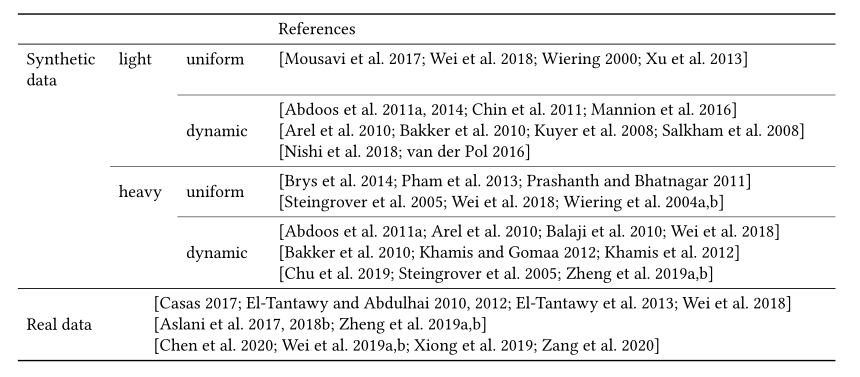
4.5.3 Traffic flow.
在交通流数据集中,每辆车被描述为 \((o,t,d)\) ,其中 \(o\) 是起点位置,\(t\) 是时间,\(d\) 是终点位置。位置 \(o\) 和 \(d\) 都是道路网上的位置。表13总结了当前研究中使用的交通流。在合成交通流数据中,\(o、t\)或 \(d\) 可以合成,以在不同等级的交通中产生均匀或动态变化的交通流。
4.6 Challenges in RL for Traffic Signal Control
当前基于RL的方法面临以下挑战:
4 . 6 . 1 RL配方的设计。
RL的一个关键问题是如何制定RL中元素的设置,即奖励和状态定义。在现有研究中[van der Pol 2016; Wei et al. 2018; Wiering 2000],交通信号控制的典型奖励定义是队列长度、等待时间和延迟等几个分量的加权线性组合。状态特征包括诸如队列长度、汽车数量、等待时间和当前交通信号相位等组成部分。近期作品中 [van der Pol 2016; Wei et al. 2018],车辆在道路上的位置的图像也被考虑在状态中。
然而,所有现有的工作都采用一种特别的方法来定义奖励和状态。这种特别的方法会导致几个问题,阻碍了RL在现实世界中的应用。首先,在制定奖励函数和状态特征时的工程细节会显著影响结果。例如,如果奖励被定义为几个项目的加权线性组合,每个项目的权重很难设置,权重设置的微小差异可能会导致显著不同的结果。第二,状态表示可以在高维空间中,特别是当使用交通图像作为状态表示的一部分时 [van der Pol 2016; Wei et al. 2018]。有了这样的高维状态表示,神经网络将需要更多的训练数据样本来学习,甚至可能不会收敛。第三,现有的RL方法和交通方法之间没有联系。没有交通理论的支持,在真实的物理世界中应用这些纯粹的数据驱动的基于RL的方法是非常危险的。
Learning efficiency. :虽然从试错中学习是强化学习的核心思想,但对于复杂的问题,强化学习的学习成本可能是不可接受的。现有的游戏强化学习方法(如围棋或雅达利游戏)通常需要大量强化学习模型的更新迭代才能在模拟环境中产生令人印象深刻的结果。这些试错的尝试会导致交通信号控制问题中真正的交通堵塞。因此,如何高效地学习(如从有限的数据样本中学习、高效探索、传递所学知识)是强化学习在交通信号控制中应用的关键问题。
Credit assignment. :奖励分配问题是 RL 中研究的热点问题之一,它考虑了一个行动的成功(或失败)的奖励分配[Sutton 1984]。在交通信号控制问题中,交通状况是交通信号控制者已经采取的几个行动的结果,这带来了两个问题:(1)一个行动经过几个步骤的行动后仍然可能有效;(2)每个时间戳的奖励是来自几个代理的后续动作的组合的结果。在雅达利(Atari)或围棋(Go)游戏中,人们有时会将一集的最终得分分配给与该集相关联的所有动作。与此不同,交通信号控制问题中的动作可能会有一个影响时间间隔,该时间间隔可能会动态变化,需要进一步研究。
Safety issue. :让强化学习智能体在物理环境中具有可接受的安全性是未来研究的另一个重要领域。虽然强化学习方法是从反复试验中学习的,但在现实世界中,强化学习的学习成本可能是至关重要的,甚至是致命的,因为交通信号的故障可能导致事故。因此,如何将风险管理引入到学习过程中,有助于防止学习过程中和学习过程后的不良行为。
5 CONCLUSION
在这篇文章中,我们介绍了交通信号控制的概述。我们首先介绍交通信号控制问题中的一些术语和目标。然后我们介绍一些经典的交通方法。接下来,我们从Rl智能体(状态、奖励、动作和协调方式)的制定及其实验设置的角度回顾了基于Rl的交通信号控制方法的现状。之后,我们简要讨论了基于RL的交通信号控制方法未来研究方向面临的挑战。希望本研究能从传统交通方法和强化学习方法两个方面提供一个全面的视角,将交通信号控制研究带入一个新的前沿。
A APPENDIX A
A.1 Summary of RL methods
表14总结了基于RL的交通信号控制方法。
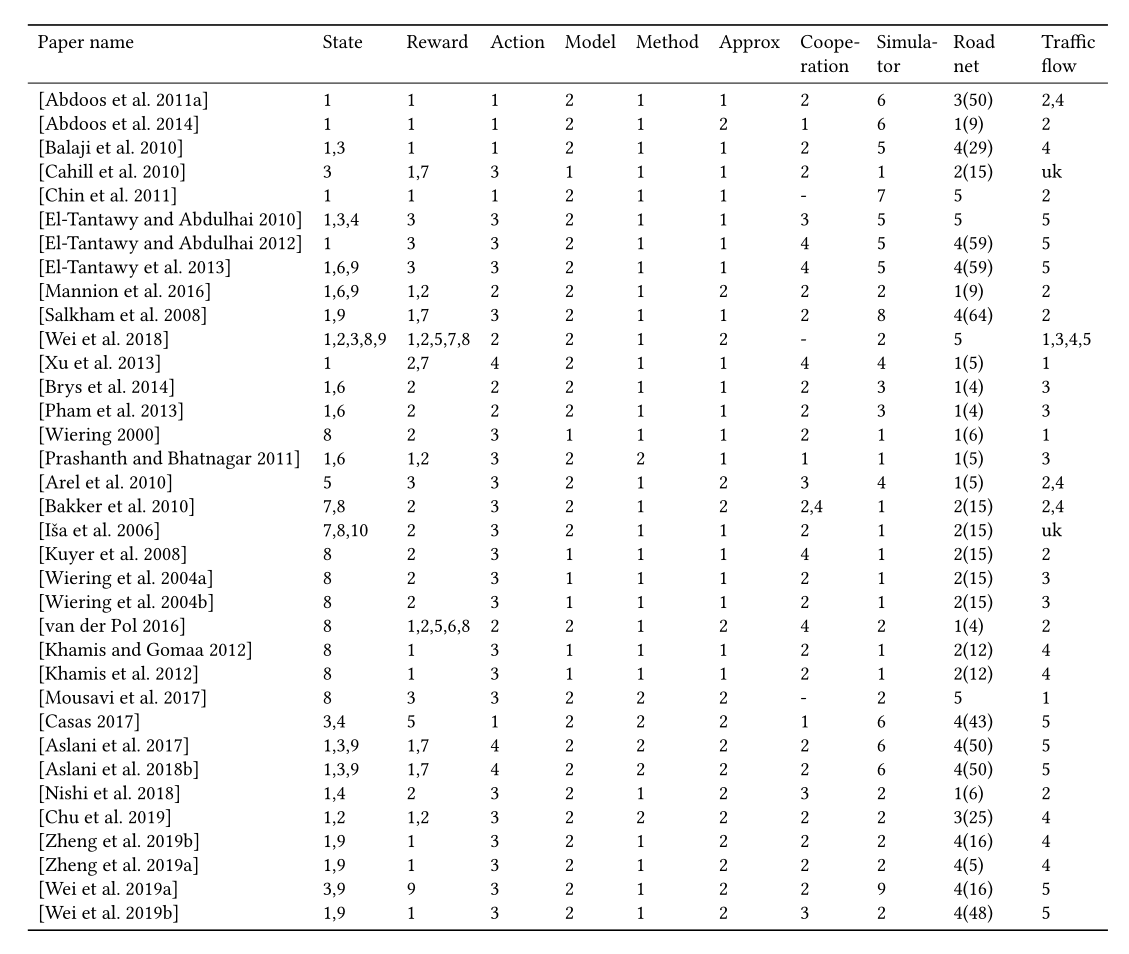
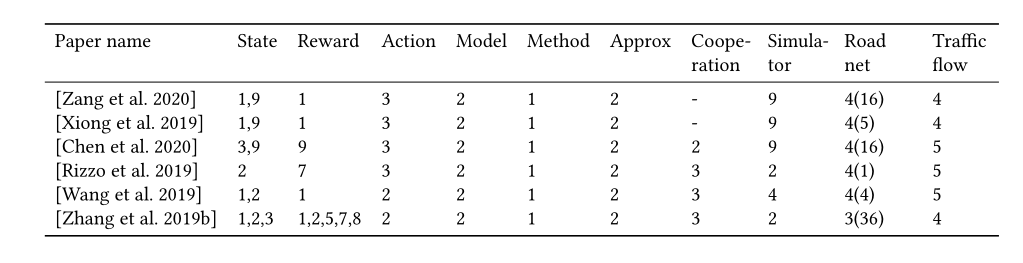
State: 1. Queue; 2. Waiting time; 3. Volume; 4. Speed; 5. Delay; 6. Elapsed time; 7. Congestion; 8. Position of vehicles; 9. Phase; 10. Accident; 11. Pressure
Reward: 1. Queue; 2. Waiting time; 3. Delay; 4. Accident; 5. Speed; 6. Number of stops; 7. Throughput 8. Frequency of signal change; 9. Pressure
Action: 1. Phase split; 2. phase switch; 3. phase itself; 4 phase duration.
Model: 1. Model-based; 2. Model-free.
Method: 1. Value-based; 2. Policy-based
Approx: 1. Tab; 2. Approx.
Cooperation: 1. Single; 2. IRL wo/ communication; 3. IRL w/ communication; 4. Joint action.
Simulation: 1. GLD; 2. SUMO; 3. AIM; 4. Matlab; 5. Paramics; 6. Aimsun; 7. QLTST; 8. UTC 9. CityFlow
Road net: 1. Synthetic <10; 2. Synthetic 11-20; 3. Synthetic >=21; 4. Real 5. Single intersection
Traffic flow: 1. Synthetic light uniform; 2. Synthetic light dynamic; 3. Synthetic heavy uniform; 4. Synthetic heavy dynamic; 5. Real-world data
REFERENCES
具体看文件
文献下载地址:https://files.cnblogs.com/files/52dxer/2020-A_Survey_on_Traffic_Signal_Control_Methods.rar


 浙公网安备 33010602011771号
浙公网安备 33010602011771号