强化学习的知识储备【更新完成】
都为笔者自己理解,加上笔者刚接触这个领域不久,因此可能存在理解偏差,希望可以和大家多多讨论,写这个知识储备的目的就是记录一下自己常用的知识,便于回顾以及查找。毕竟自己记录的知识,回顾起来自己写的什么意思最容易理解。
本文中的图片都源于百度AI studio课程: 强化学习7日打卡营-世界冠军带你从零实践
Behavior Policy(行为策略 )和Target Policy(目标策略)
Behavior Policy: 行为策略是用来与环境互动产生数据的策略 , 即在训练过程中做决策 。例如智能体不断的与环境交互,更新Q表格中的Q值。
Target Policy: 在行为策略产生的数据中不断学习、优化,即学习训练完毕后拿去应用的策略。 也就是智能体根据Q表格中的数据进行学习,判断在每个状态下发起什么动作。
exploitation(利用) 和 exploration (探索)
exploitation:利用就是根据已有的经验去取得最大回报。比如,附近有十家餐馆,你已经去过里边的七家了,你知道这七家中红烧排骨最好吃,所以你会根据已有经验去吃红烧排骨,也不会去尝试另外的三家餐馆。这样是局部最优解。
exploration:探索是指做你以前从来没有做过的事情,以期望获得更高的回报。 这时候你就要去尝试剩下的三家餐馆,看看有没有更好吃的菜,去寻找全局最优解。
贪婪策略和e-greedy贪婪策略
贪婪策略:是一个确定性的策略,每一次都选择回报价值最大的那个策略。
e-greedy贪婪策略:是一个不确定性的策略,平衡了利用和探索,其中选取动作值函数最大的部分为利用,仍有概率去寻找全局最优解为探索部分。令e=0.1,也就是有1-0.1=0.9的概率是利用,有0.1的概率是探索。
也就是选择当前最大回报的概率是0.9,去寻找全局最优解进行探索的概率是0.1.
On-Policy(Sarsa)&Off-Policy(Q-learning)
On-Policy:典型的算法就是Sarsa,获取数据的动作和最终策略的动作是一致的。只有一个策略π,使用策略π去与环境产生经验,使用策略π去学习,因为需要兼顾利用与探索,因此策略π并不稳定。
# Sarsa 算法
initialize Q(s,a) randomly
for each episode:
initialize state s;
choose action a from s using ε-greedy strategy;
while s is not terminal:
observe reward r and next state s';
choose a' from s' using ε-greedy strategy;
Q(s,a) = Q(s,a) + α[r + γ*Q(s',a') - Q(s,a)];
s = s', a = a';
Off-Policy : 典型的算法就是Q-learning,获取数据的动作和最终策略的动作不一定一致,是因为有一个随机的概率去选择探索全局最优解。有两个策略,一个目标策略π,一个行为策略μ,目标策略π用来学习最优策略,行为策略μ更具有探索性,与环境交互产生经验。
# Q-learning 算法
initialize Q(s,a) randomly
for each episode:
initialize state s;
while s is not terminal:
choose action a from s using ε-greedy strategy;
observe reward r and next state s';
Q(s,a) = Q(s,a) + α[r + γ*maxQ(s',a') - Q(s,a)];
s = s';
总结:两个算法的主要区别就是在倒数第二行Q值更新那里,还有Sarsa算法直接将a‘的值赋给a,也就是Sarsa是直接选择下个动作去执行。Q-learning在计算下一状态的预期收益时利用了max操作,也就是直接选择下一状态的最优动作,获取最大回报。但是实际过程中因为有e-greedy策略,有小概率选择探索,不会去选择当前最优的动作,所以学习时的policy(行为策略)和生成样本的policy(目标策略)不一定相同,为off-policy算法。Sarsa则是直接选择下一次动作去执行,它只有一种策略,用同种策略去做选取,去做优化。就算下一步是选择探索,并且掉进了悬崖(迷宫问题,掉进悬崖就给一个负的reward),它也会去执行,会把悬崖附近的Q值更新为负的,因此在迷宫问题中,它会离悬崖远远的。因为学习时的policy和预测时的policy一致,因此为on-policy
软更新和硬更新
软更新应该是指每次更新参数的时候利用一个衰减的比例
硬更新则是指每隔一定步数完全Copy参数
DQN=神经网络+Q-learning,两大创新点:经验回放,固定Q目标
先说一下Q-learning算法,在Q-learning中我们有一个Q(s,a)函数,用来通过输入状态s,和动作a,来得到奖励回报reward
我们在特定状态下,采取奖励回报最高的动作,那么我们可以构建一个最大化回报的策略:
对于我们的训练规则,当前的总奖励Qπ(这个是预测的总奖励)就等于当前动作的回报r加上衰减因子gamma乘上未来的总奖励。假设我们的策略的Q函数都遵循贝尔曼方:
等式两边的差异,称为时间差异:
我们就来降低这个时间差异,让预测的奖励尽可能的接近
经验回放:优点1:打乱样本关联性,对于神经网络输入的样本都是独立的,各个样本之间没有什么关联性。因为强化学习是一个i训练决策的过程,所以前后的状态是相互影响,相互关联的,所以打断样本之间的关联性,才会更好的使用神经网络,DQN就是利用了Q-learning的off-policy 的特点,它设置一个经验池,先存取一批的经验数据,然后随机从经验池里选取一个batch数据,来更新网络。还可以提高数据利用率,因为经验池中的数据可能会多次被抽取,因为智能体与环境交互拿到的数据量是比较少的,通过经验池这样存起来,多用几次,就不会浪费。(就像现实环境中,有些事情会多次学习一样)
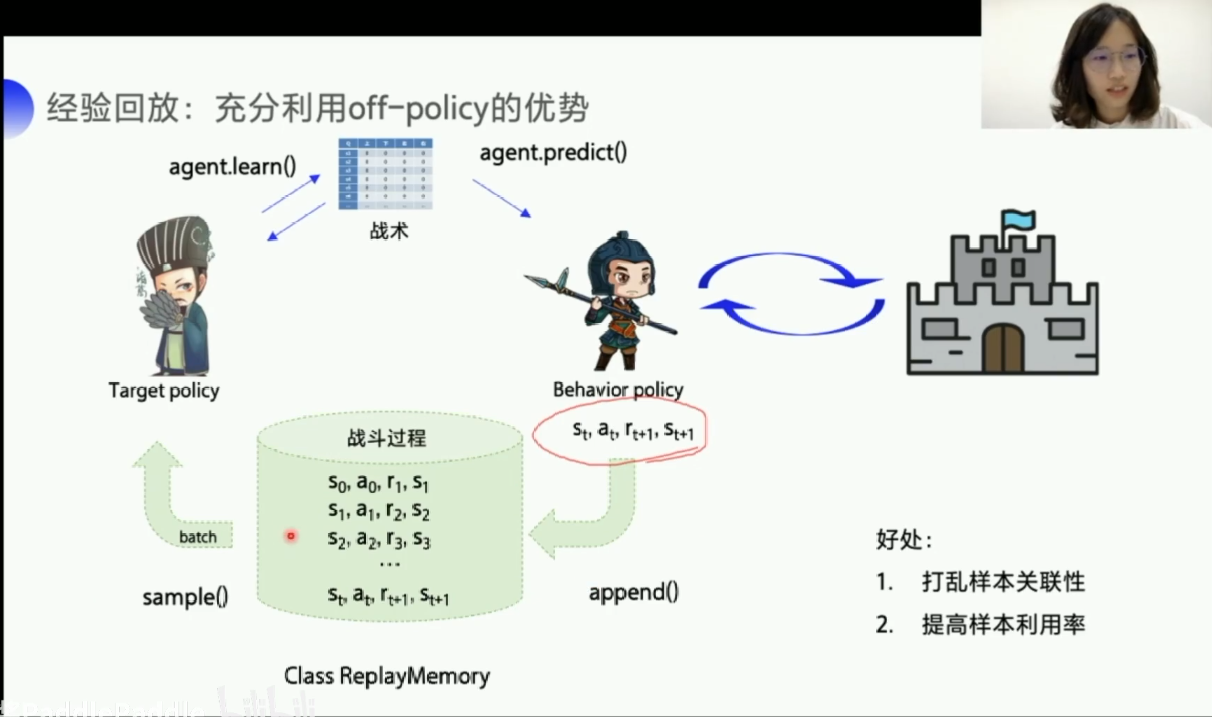
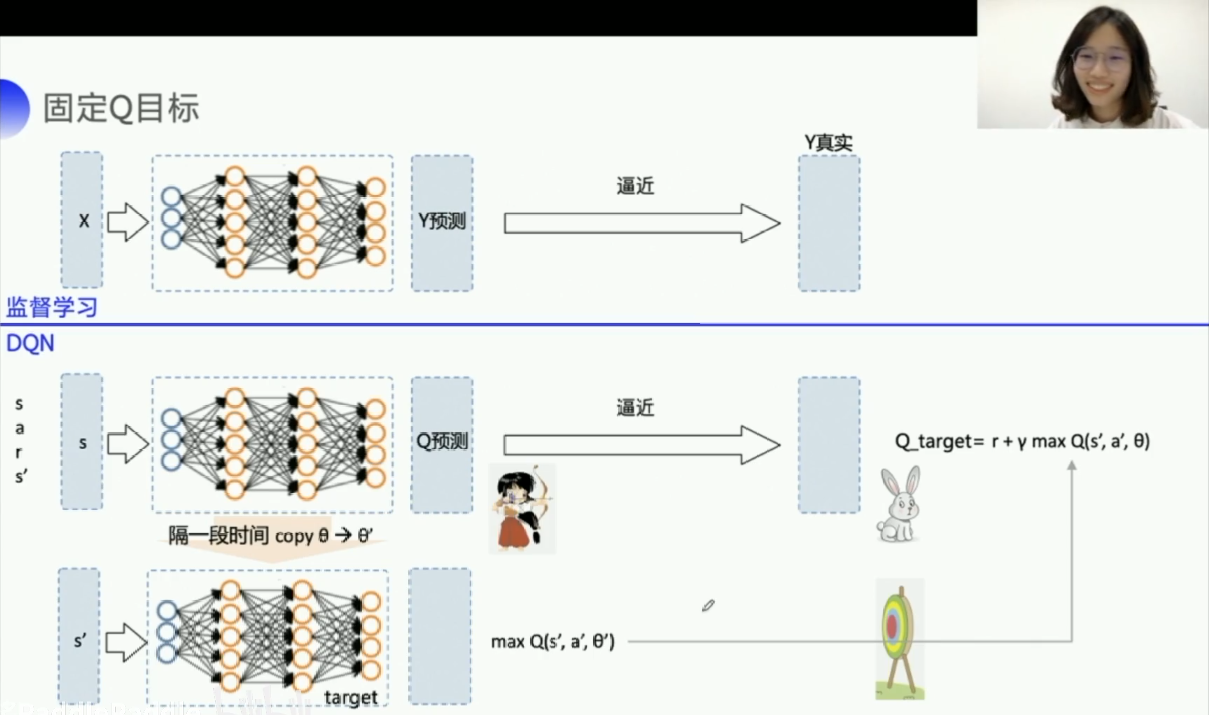
固定Q目标 :解决了算法更新不平稳的问题,在监督学习中,预测的真实值是固定不变的,因此逼近的时候,也比较稳定,但是在DQN中,Q_target是由下一步的(s',a')不断更新的,想要让Q_predict值逼近Q_target值,但是Q_target又一直变换,因为造成了不稳定的结果。DQN就提出了使用一个临时的Q_temp来固定一下Q_target的值,然后隔段时间再将Q_temp更新为Q_target的值,这样每隔一段时间更新Q_temp值为Q_target的值,就达到了稳定的效果。
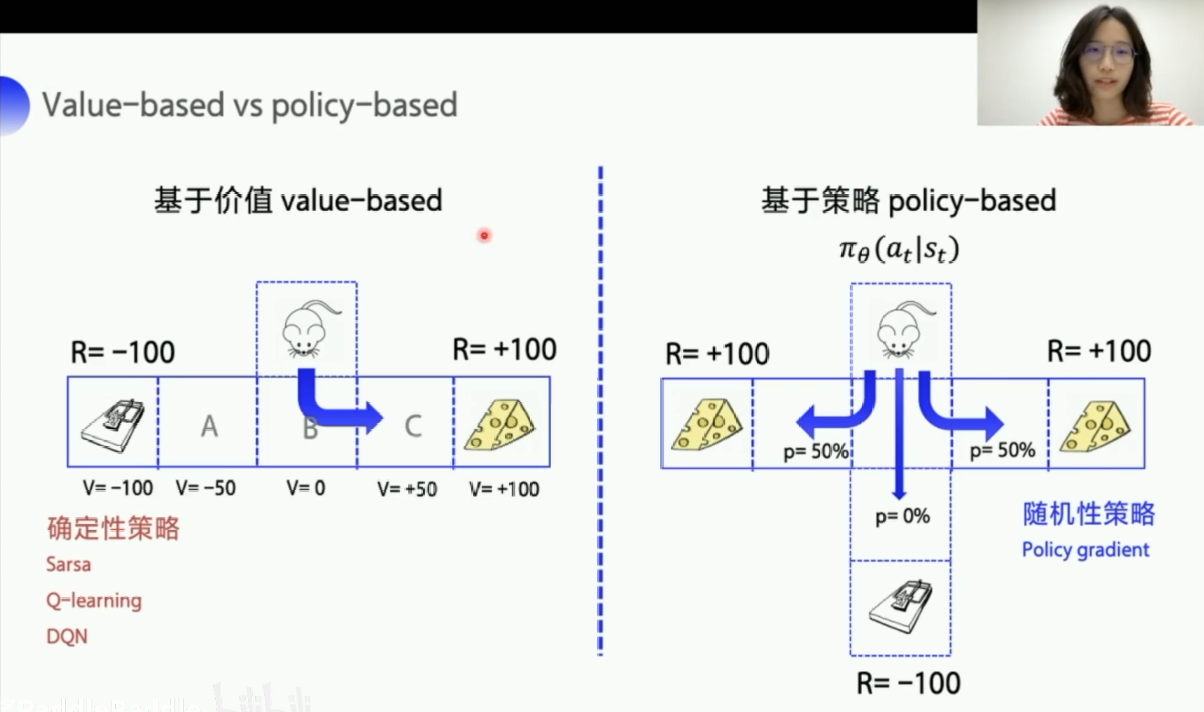
Value-based 和 policy-based
Value-based:先学习动作价值函数,训练的目的是为了将Q值迭代更新到最优,然后再根据每一步的价值选择最优的动作。1. 先优化Q值,然后选择Q值最大的那个action。2. 是一个确定性的策略,到达最优之后,参数就固定下来了,那么输入一样的状态的话,得到的action是一样的。
policy-based :直接学习动作概率,动作的选择不再依赖于价值函数,而是根据一个策略走到底,看最后的总收益来判断这个策略是好还是坏。1. 直接一步到位,神经网络直接输出action。2. 得到的是动作的概率,是一个随机的策略,假设一共三种动作,可能a1的概率 p(a1|s) = 0.3,a2的概率 p(a2|s) = 0.6,a3的概率p(a3|s) = 0.1。那么根据概率随机的采样一个动作输出,一般会在最后选择action之前加入一个softmax激活函数,softmax函数讲解在这里:点击跳转
value-based模型步骤:
首先我们基于状态s1,用 e-greedy法选择到动作a1,然后执行动作a1 ,得到奖励R1 ,并进入状态s2 ;然后基于状态s2 ,使用贪婪法选择 a2,也就是说,选择使 Q(s2,a)最大的 a作为 a2来更新价值函数。用数学公式表示就是:
经过上边的公式,不断的更新Q表格(Q表格:一共有len(state)行,len(action)列,对应的是每个状态下选择某个动作,所获得的Q值)。在训练时,会有e-greedy概率,去选择探索,但在最终测试时,所有的动作都选择利用,这样才能利用已知经验获得最佳效果,利用和探索在上边讲解了,一定要好好理解啊,用到的非常多。
policy-based模型步骤:
从第一个状态,选择动作,到下一个状态,在选择动作,再到下一个状态,如此循环,不断的交互,等交互终止了之后,我们就称我们完成了一个episode,这样一场游戏结束,我们把这一整个episode里边所有的s和a串起来的集合就叫一个episode的轨迹,Trajectory:
有了这条轨迹,那么我们就可以计算这条轨迹发生的概率,也就是把里边的每一个概率都连乘起来:
还可以计算这条轨迹的总回报:每一个step的回报累加起来。
π(a|s)的期望回报:所有episode的平均回报,但是很多环境中轨迹有无数条,不可能穷举每一个episode,所以我们求N个episode,然后求平均,当N足够大的时候,我们就可以用后边的近似的去拟合Rθ,这个过程我们称之为采样,采样N个episode来计算我们的期望回报。
这个期望回报就是我们能够用来优化策略函数的目标。
Value-based 和 policy-based的优化策略函数比较:
Value-based:一般采用时序差分的优化方式优化目标:优化两者之间的差值,越小越好。
policy-based:一般采用蒙特卡洛策略梯度的优化方式优化目标:优化期望回报,希望越大越好,梯度上升。
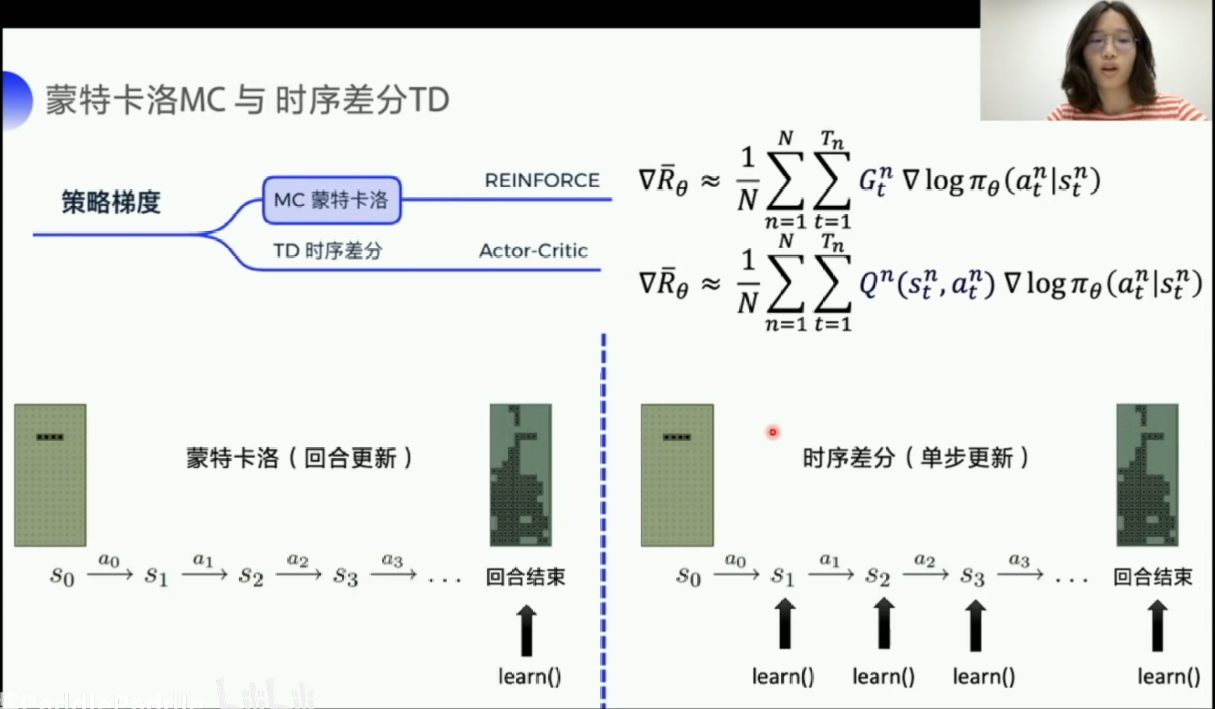
蒙特卡洛(MC) 和 时序差分 (TD)
蒙特卡洛:是回合更新,当进行完整个回合后,才会进行一次更新,所以更新速度比较慢。
时序差分 :单步更新,没走一步,都进行一次更新,所以更新频率比较高。
利用交叉熵优化Policy Gradient:梯度上升
- 交叉熵就是一个可以用来计算两个分布之间的差值的方法。
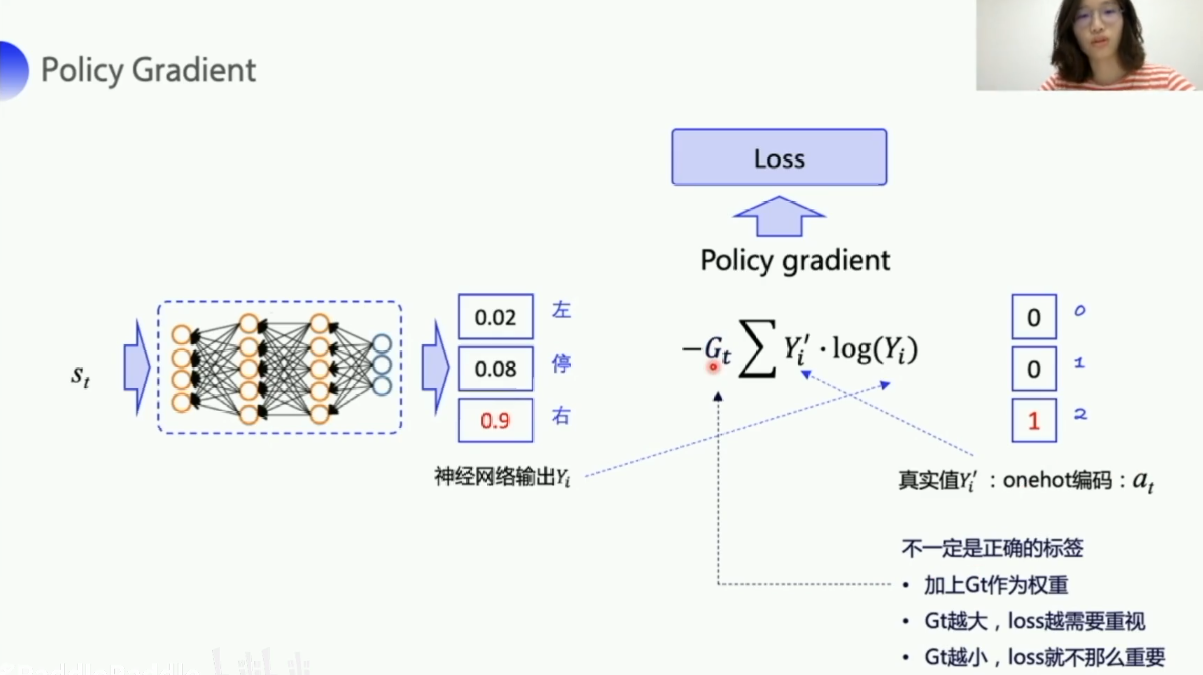
如图,在状态st下,有三个动作,a1概率为0.02,a2概率为0.08,a3概率为0.9,可以看出来a3的概率最大,也是Gt最大的,得到的回报最高,因此我们就越需要优化a3,右边one-hot编码中的at只是执行的action,是真实的action,但不一定是正确的action,不能作为一个正确的标签来知道我们的神经网络朝着正确的方向去更新。所以我们在这里需要乘以一个奖励回报,这个奖励回报相当于对右边这个真实的action 的一个评价,Gt越大,未来的总收益越大,就说明当前选择的这个action就越好。那我这个loss就越需要重视,如果Gt很小,那么就说明有点这个真实的action并没有那么好,那我的loss 的权重就小一点,优化的力度就小一点。我们是想我们的期望回报越高越好,也就是梯度上升的方式,因为框架中优化器都是以梯度下降的方式优化的,所以我们在公式前边加上一个负号。
REINFORCE模型:
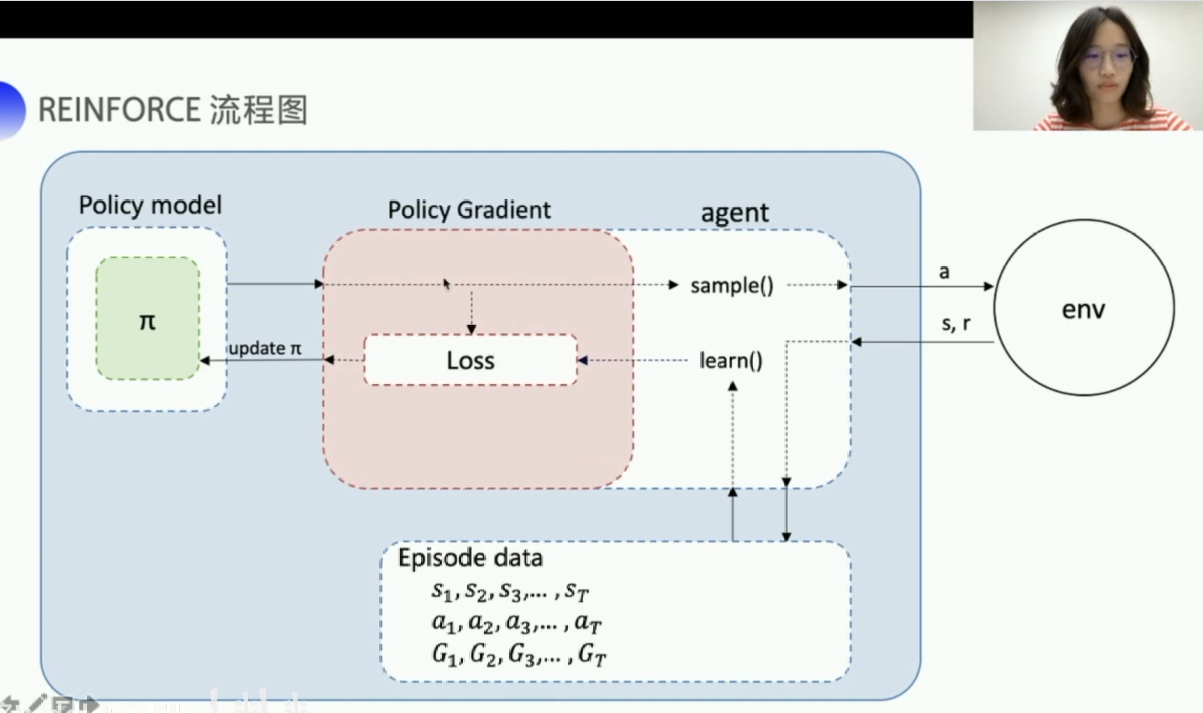
REINFORCE模型的流程图:
-
更新的过程如下:
智能体先选择action去和环境交互,然后环境反馈给智能体s,r,这样就得到了(s,a,r)这样的字典。
然后将每一个reward转化成后缀和形式,计算后缀和Gt的代码实现如下:
# 计算后缀和 def suffix_sum(reward_list,gamma=1.0): """ range(4,-1,-1): (4,3,2,1,0) """ for i in range(len(reward_list)-2,-1,-1): """ r[4]+=γr[5] r[3]+=γr[4] r[2]+=γr[3] r[1]+=γr[2] r[0]+=γr[1] """ reward_list[i]+=gamma*reward_list[i+1] return np.array(reward_list)计算完后缀和后就有了一个这样的数据,每一个状态下的动作,对应的后边的总回报,也就是流程图中的Episode data。
\[reward\_list=\{(s_1,a_1,G_1),(s_2,a_2,G_2),(s_3,a_3,G_3)...\} \]到了这一步后,我们现在就可以先从神经网络中拿到某个状态下每个action的概率,然后上边reward_list就是我们实际的action(实际的action但不一定是正确的action),把这个action转换成one-hot向量,然后根据下式去learn(),来计算两个分布之间的Loss
\[Loss=-G_t \ \ \ \ *\underbrace{[0,1,0,0,0,0]}_{\rm 实际的action,但不一定是正确的action}* \ \ \ \ \ \ \ \ \underbrace{log[0.2,0.5,0.05,0.1,0.05,0.1]}_{\rm经过神经网络最后的softmax后的\pi(a|s,\theta)} \]得到这个Loss后,就可以用来去更新模型中的策略π。
离散动作和连续动作
离散动作:就是action的数量是可数的,例如迷宫问题里的action就只有上下左右。
离散动作的随机性策略πθ(at|st),通过输入状态s,在神经网络的最后边加入一层softmax层,得到选择每个action的概率。
连续动作:action的数量是不可数的,例如无人驾驶中,汽车方向盘转动的角度等等。
连续动作的确定性策略μθ(st),就是输入同样的状态s,输出同样的action,通过输入状态s,在神经网络最后边加入一层tanh层,将输出的action缩放到 [-1,1],然后再进行一个scale(缩放)过程,把action缩放到指定的范围内,例如小车的一个速度问题,在状态s下,经过tanh层后得到一个action=0.9,假设小车的速度是 [-5,5],然后经过一个scale方法,将action=0.9*5=4.5,假设action是小车的速度,就让小车的速度设置为4.5。
DDPG( Deep Deterministic Policy Gradient ):DQN的升级版,用来接触连续动作
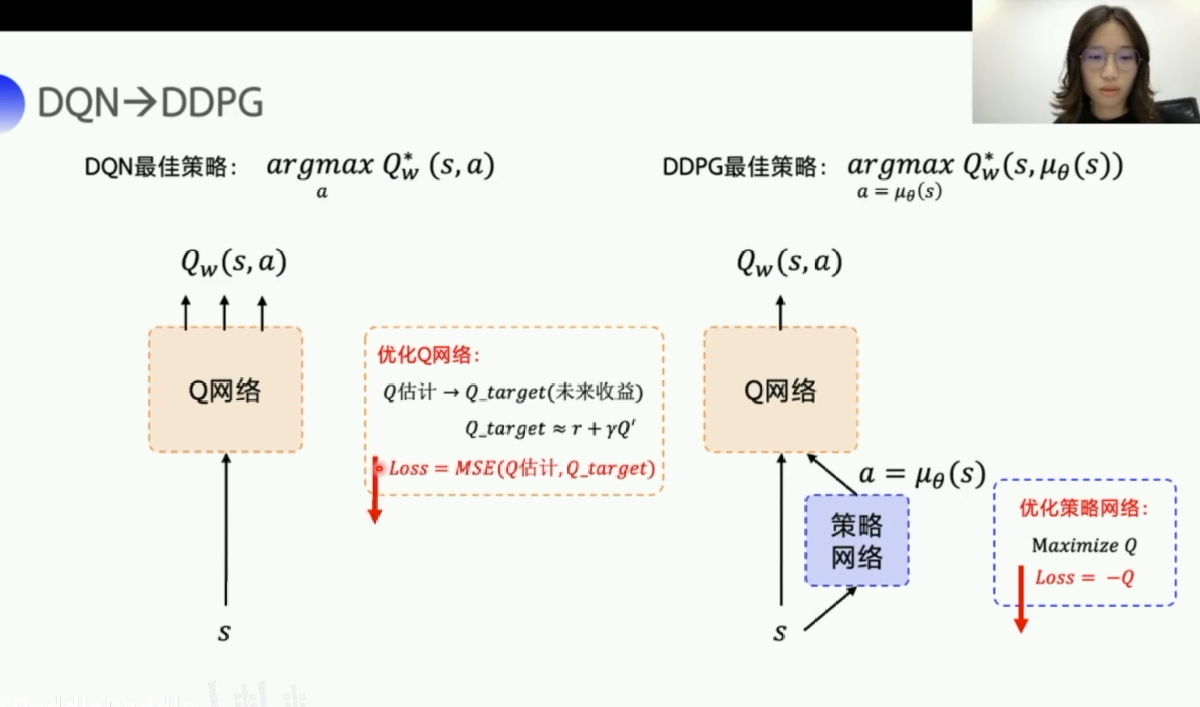
DQN:是在Q-learning的基础上,加入了一个Q网络,Q网络主要的作用就是,通过输入状态s,然后来求得Q预测,也就是Q_w(s,a)。
Q网络输出的Q预测,我们用环境反馈的reward和下一步的Q预测来去拟合未来的收益,未来的收益也就是Q_target,然后让Q网络的输出Q估计去靠近Q_target。最后通过计算Q估计和Q_target之间的均方差Loss,来优化Q网络:
DDPG:因为要处理连续的动作,所以DDPG是在DQN的基础上,再加入了一个策略网络,策略网络就是通过输入状态s然后来求得动作a=μθ(s) ,再把a交给Q网络,然后Q网络有了 (s,a),就来计算Q预测,也就是Q_w(s,a)。DDPG的这种结构称为actor-critic结构,策略网络就是扮演的actor的角色,用来对外输出动作,然后Q网络就是扮演的critic,用来给actor所输出的动作打分,而环境的反馈reward,来用评估critic的打分策略,简单来说就是环境反馈reward优化Q网络,Q网络优化策略网络。刚开始的时候Q网络和策略网络都是随机的,然后因为有环境的反馈reward,所以critic的打分会越来越准确,然后也会带着actor的表现越来越好。
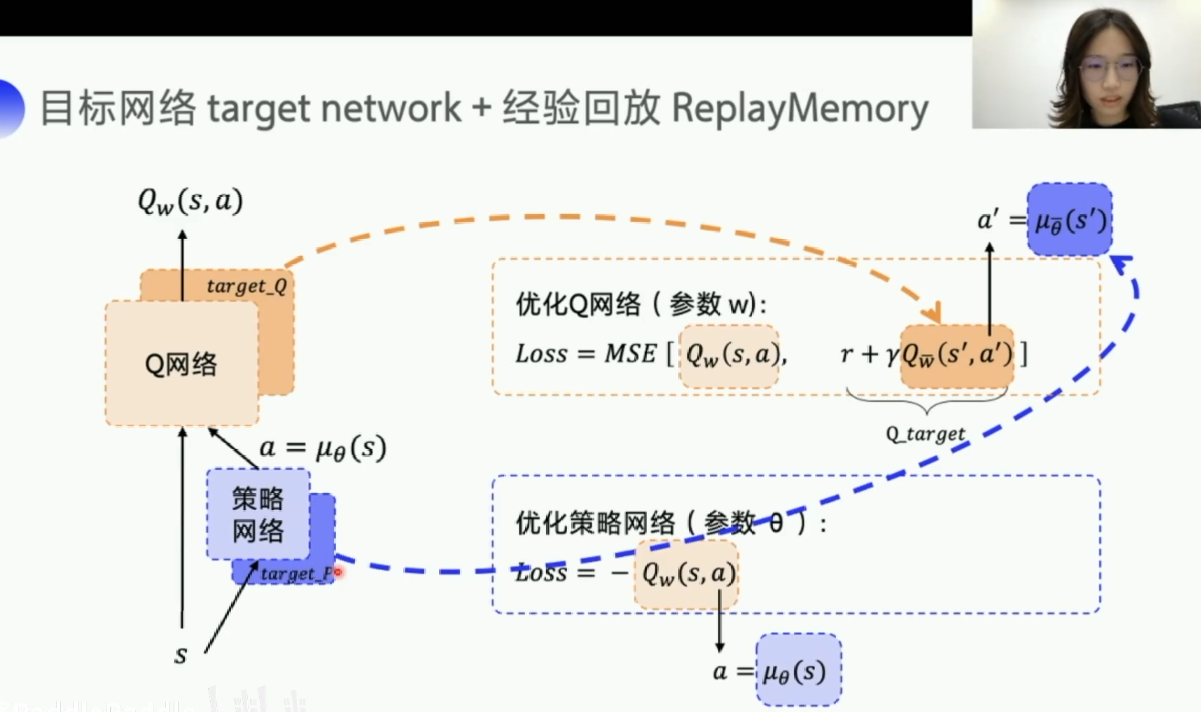
在DDPG中我们有两个网络需要优化,一个是策略网络,一个是Q网络,这两个网络我们分别用两个参数来表示要优化的内容,优化策略网络(参数θ),优化Q网络(参数w),具体看下图。
-
优化策略网络中,策略网络的目标就是选择一个最优的action,然后让Q_w(s,a)越大越好,通过策略网络求出a=μθ(s),然后用Loss=-Q_w(s,a)来计算损失,也就是然后放到优化器里,让优化器自动用梯度下降的方法来进行优化,优化器优化Loss越低,也就是Q_w(s,a)越大,与目标是一样的。
-
优化Q网络中,Q网络的目标是让Q预测逼近Q_target。
\[\begin{align}& Q预测 =Q_w(s,a)\\& Q_{target}=r+\gamma Q_{\bar w}(s',a')\\Loss & =MSE[Q预测,Q_{target}]\\& =MSE[Q_w(s,a),r+\gamma Q_{\bar w}(s',a')]\end{align} \]
DDPG代码模型的总体架构:
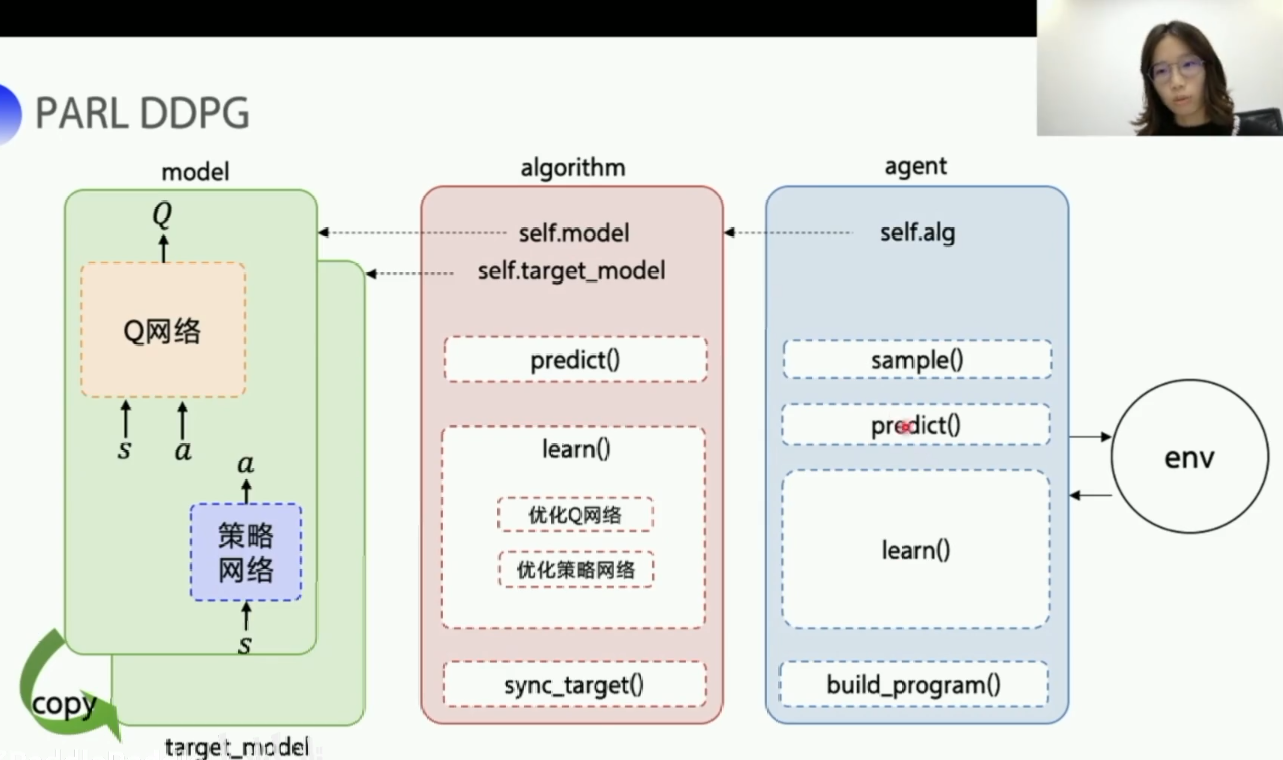
DDPG中的固定Q目标和经验回放ReplayMemory
固定Q目标:在DQN中,因为每一个状态下,每个动作的Q_target是变化的,这样你如果用Q预测去靠近一个变化的Q_target,那就不容易收敛,因此我们就用一个临时的Q_temp来固定一下Q_target,然后每隔一段时间,再去更新Q_temp的值为Q_target,在DDPG中,我们同样也是需要固定Q_target,因为Q_target是由a'来求得的,而a'是我们用策略网络求得的,a'在每一个状态转变的过程中也是变化的,所以我们还需要固定一下a', 我们分别在target网络中的参数上加一个横杠,来区分开来。target_Q和target_P我们统称为target网络。
经验回放:参考DQN,和DQN中的内容一样。
最后是后续学习的资料推荐,包括理论,动手实践,进阶论文,前沿研究方向,强化学习道阻且长,最后再强调一遍,本文中的图片都源于百度AI studio课程: 强化学习7日打卡营-世界冠军带你从零实践 ,讲课很棒,让我对强化学习的入门有了一个清楚的认识,PPT做的也很好,结合PPT的讲解,能让人更加理解,不理解的地方,多看两边,然后动手把她说的话打一遍,再看看,就能理解了。


