吴恩达机器学习课后作业ex1
题目大体意思就是输入的是某地的人口,输出的是某地方的收益。
题目及数据集下载:
https://wwa.lanzous.com/b054sprza 密码:ba3w
大体模型如下图:现在X前边加一列值为1的列,然后求解两个参数theta1和theta2,这样求解和y=kx+b,求k与b一样,只不过是通过下边这种方法求解,模型更有适应性,可以更适应其他相似的模型。

1.计算损失
1.1计算损失的公式:
\[loss={(X_{i1}\theta1+X_{i2}\theta2-Y_{i1})}^{2}
\]
# 计算损失
def computeLoss(x, y, theta):
error=np.power(x.dot(theta) - y, 2)
# print(error)
return np.sum(error)/(2*len(X))
2.多变量梯度下降
2.1根据上边计算损失的公式求导得计算梯度的公式:
\[\frac{\partial{loss}}{\partial{\theta1}}=\frac{1}{N}\sum_{i=1}^{n}{(X_{i1}\theta1+X_{i2}\theta2-Y_{i1})}*X_{i1}
\]
\[\frac{\partial{loss}}{\partial{\theta2}}=\frac{1}{N}\sum_{i=1}^{n}{(X_{i1}\theta1+X_{i2}\theta2-Y_{i1})}*X_{i2}
\]
代码里边各个元素的含义:
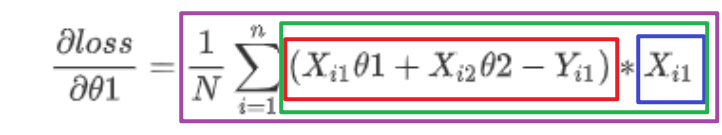
error:红框
xj:蓝框
term:绿框
temp:紫框
# 多变量梯度下降
def gradient(x,y,theta,learningrate,iters):
temp = np.zeros(theta.shape) # [2,1]
param = theta.size # 要学习参数的个数,2
for i in range(iters):
error = x @ theta - y # 数学矩阵相乘,[97,2]@[2,1]=[97,1]
for j in range(param):
xj=x[:,j].reshape(np.shape(x)[0],1) # 取X的第j列,[97,1]
term = error*xj # 对应元素相乘,[97,1]*[97,1]=[97,1]
temp[j,0]=theta[j,0]-learningrate*np.sum(term)/len(x) # 计算所有的损失和
theta = temp
return theta
最后的总代码:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
lr=0.01 # 训练速率
Iters = 5000 # 训练次数
# 计算损失
def computeLoss(x, y, theta):
loss=np.power(x.dot(theta) - y, 2)
return np.sum(loss)/(2*len(X))
# 多变量梯度下降
def gradient(x,y,theta,learningrate,iters):
temp = np.zeros(theta.shape) # [2,1]
param = theta.size # 要学习参数的个数,2
for i in range(iters):
error = x @ theta - y # 数学矩阵相乘,[97,2]@[2,1]=[97,1]
for j in range(param):
xj=x[:,j].reshape(np.shape(x)[0],1) # 取X的第j列,[97,1]
term = error*xj # 对应元素相乘,[97,1]*[97,1]=[97,1]
temp[j,0]=theta[j,0]-learningrate*np.sum(term)/len(x) # 计算所有的损失和
theta = temp
return theta
if __name__ == '__main__':
# 1.1先拿到数据
path='ex1data1.txt'
data=pd.read_csv(path,header=None,names=['Population','Profit'])
# 1.2看一下数据大体什么样子
print(data.head())
print(data.describe())
# 1.3进行数据处理,在数据第0列前边加一列
data.insert(0,'Ones',1)
print(data.head())
# 1.4将X和Y分开,
cols=data.shape[1]
X=data.iloc[:,0:cols-1]
Y=data.iloc[:,cols-1:]
print(X.head())
print(Y.head())
# 1.5将数据转换成numpy格式
X=np.array(X)
Y=np.array(Y)
# 创建要训练的参数,并设置成两行一列向量
theta=np.array([1,1]).reshape([2,1])
# 1.6再看一下数据的各个形状
print(X.shape,Y.shape,theta.shape)
print(theta)
# 2.计算损失
print(computeLoss(X,Y,theta))
# 3.优化损失
theta=gradient(X,Y,theta,lr,Iters)
print(theta)
print(computeLoss(X,Y,theta))
# 求得最后的损失为4.476971407448775
# 求得theta1和theta2为[-3.8951929 , 1.19297458]
# 4.用plt绘制一下最后的图形
# 绘制直线
x = np.arange(5, 22.5)
y = theta[0]+x*theta[1]
plt.plot(x, y)
# 绘制散点
plt.scatter(X[:,1], Y)
plt.show()

