Pytorch-tensor的感知机,链式法则
1.单层感知机
单层感知机的主要步骤:
- 1.对数据进行一个权重的累加求和,求得
∑ - 2.将
∑经过一个激活函数Sigmoid,得出值O - 3.再将
O,经过一个损失函数mse_loss,得出值loss - 4.根据
loss,以及前边所求得的值,求得loss对各个w的偏导数 - 5.更新
w值
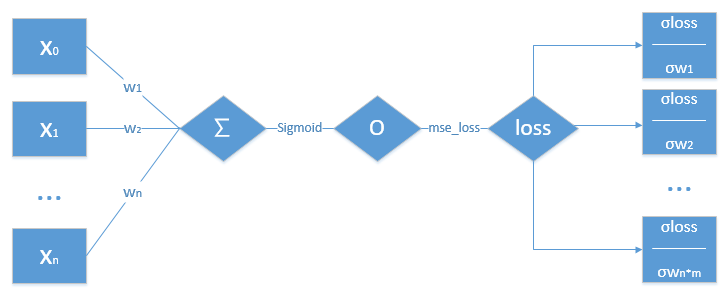
# 单层感知机梯度的推导
# 要进行优化的是w,对w进行梯度下降
a=torch.randn(1,10)
# a是一个【1,10】的向量
w=torch.randn(1,10,requires_grad=True)
# w是一个可导的【1,10】的向量
# 1.2.经过一个sigmoid激活函数
o=torch.sigmoid(a@w.t())
print(o.shape)
# 3.经过一个mse_loss损失函数
# loss是一个标量
loss=F.mse_loss(torch.ones(1,1),o)
print(loss.shape)
# 4.求loss对w0,w1....w9的偏导数
loss.backward()
print(w.grad)
# 5.后边就可以对w进行梯度更新
输出结果
torch.Size([1, 1])
torch.Size([])
tensor([[ 3.6432e-05, -7.3545e-05, -4.3179e-05, 3.3986e-04, -9.5312e-05,
-1.7416e-04, -1.7869e-05, -2.3893e-04, -1.5513e-04, -2.1554e-05]])
多层感知机的主要步骤:
-
1.对数据进行一个权重的累加求和,求得
∑1,∑2,,,∑m -
2.将
∑1,∑2,,,∑m经过一个激活函数Sigmoid,得出值O1,O2,,,Om -
3.再将
O1,O2,,,Om,经过一个损失函数mse_loss,得出值loss -
4.根据
loss,以及前边所求得的值,求得loss对各个w的偏导数 -
5.更新
w值
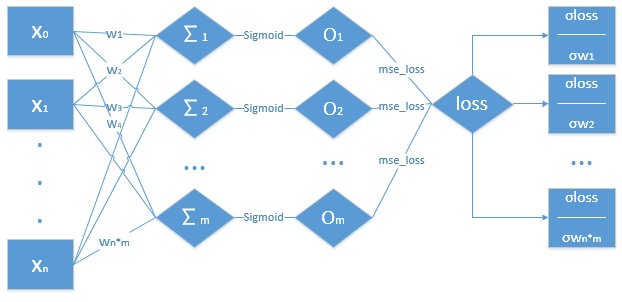
# 多层感知机梯度的推导
# 要进行优化的是w,对w进行梯度下降
a=torch.randn(1,10)
# a是一个【1,10】的向量
w=torch.randn(2,10,requires_grad=True)
# w是一个可导的【2,10】的向量
# 1.2.经过一个sigmoid激活函数
o=torch.sigmoid(a@w.t())
print(o.shape)
# 3.经过一个mse_loss损失函数
# loss是一个标量
loss=F.mse_loss(torch.ones(1,2),o)
print(loss)
# 4.求loss对w0,w1....w9的偏导数
loss.backward()
print(w.grad)
# 5.后边就可以对w进行梯度更新
输出结果
torch.Size([1, 2])
tensor(0.2823, grad_fn=<MeanBackward0>)
tensor([[-0.0654, 0.0242, 0.0045, -0.1007, 0.0259, -0.0522, -0.0327, 0.0805,-0.0180,-0.0186],
[-0.1300, 0.0481, 0.0090, -0.2002, 0.0514, -0.1037, -0.0650, 0.1599,-0.0358,-0.0371]])
链式法则:
y=f(u),u=f(x),y对x的导数,可以通过u来中间传递,也就是说
dy/dx=(dy/du)*(du/dx)
x=torch.rand(1)
w1=torch.rand(1,requires_grad=True)
b1=torch.rand(1)
w2=torch.rand(1,requires_grad=True)
b2=torch.rand(1)
y1=x*w1+b1
y2=y1*w2+b2
dy1_dw1=torch.autograd.grad(y1,[w1],retain_graph=True)[0]
dy2_dy1=torch.autograd.grad(y2,[y1],retain_graph=True)[0]
dy2_dw1=torch.autograd.grad(y2,[w1],retain_graph=True)[0]
print(dy1_dw1*dy2_dy1)
print(dy2_dw1)
输出结果
tensor([0.1867])
tensor([0.1867])

