Pytorch-tensor的激活函数
1.激活函数
激活函数的作用是能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。因为很多问题都不是线性的,你只有给它加入一些非线性因素,就能够让问题更好的解决。
函数1:RELU():
优点:
- 1.相比起Sigmoid和tanh,在SGD中能够快速收敛。
- 2.有效缓解了梯度弥散的问题。

a=torch.linspace(-1,1,10)
print(a)
# relu()小于0的都归为0,大于0的成线性
print(torch.relu(a))
输出结果
tensor([-1.0000, -0.7778, -0.5556, -0.333
3, -0.1111, 0.1111, 0.3333, 0.5556,
0.7778, 1.0000])
tensor([0.0000, 0.0000, 0.0000, 0.0000, 0
.0000, 0.1111, 0.3333, 0.5556, 0.7778,
1.0000])
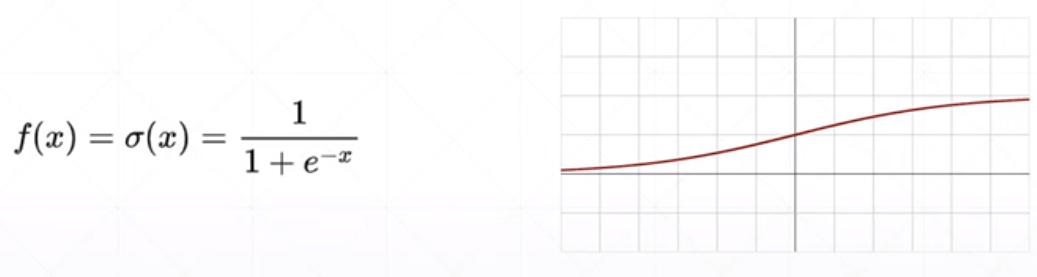
函数2:Sigmoid():
优点:
- 1.Sigmoid函数的输出映射在之间,单调连续,输出范围有限,优化稳定,可以用作输出层。
- 2.求导比较容易。
缺点:
- 1.在两个极端,容易出现梯度弥散。
- 2.其输出并不是以0为中心的。
a=torch.linspace(-100,100,10)
print(a)
# relu()小于0的都归为0,大于0的成线性
print(torch.sigmoid(a))
输出结果
tensor([-100.0000, -77.7778, -55.5556,
-33.3333, -11.1111, 11.1111,
33.3333, 55.5556, 77.7778,
100.0000])
tensor([0.0000e+00, 1.6655e-34, 7.4564e-2
5, 3.3382e-15, 1.4945e-05, 9.9999e-01,
1.0000e+00, 1.0000e+00, 1.0000e+0
0, 1.0000e+00])
函数3:Tanh():
优点:
- 1.比Sigmoid函数收敛速度更快。
- 2.相比Sigmoid函数,其输出以0为中心。
缺点:
- 仍然存在由于饱和性产生的梯度弥散。

a=torch.linspace(-10,10,10)
print(a)
# relu()小于0的都归为0,大于0的成线性
print(torch.tanh(a))
输出结果
tensor([-10.0000, -7.7778, -5.5556, -3
.3333, -1.1111, 1.1111, 3.3333,
5.5556, 7.7778, 10.0000])
tensor([-1.0000, -1.0000, -1.0000, -0.997
5, -0.8045, 0.8045, 0.9975, 1.0000,
1.0000, 1.0000])
函数4:Softmax():
softmax通俗理解的大体意思就是,Z1,Z2,,,Zn中,所有的值,先进行一个e^Zi变换,得到yi,然后在除以所有yi的累加和,得到每个值在整个数组中的比重。经过一次sofymax()函数之后,会放大值与值之间的比例,例如图中的Z1,Z2,经过softmax函数之前,是3:1,经过之后,就变成了0.88:0.12。
作用:将张量的每个元素缩放到(0,1)区间且和为1
下图详细讲解了softmax是怎么计算的,图源于网络。

图中例子代码实现如下:
import torch
import torch.nn.functional as F
if __name__ == '__main__':
data=torch.tensor([3.0,1.0,-3.0])
print(data)
y=F.softmax(data,dim=0)
print(y)
输出结果
tensor([ 3., 1., -3.])
tensor([0.8789, 0.1189, 0.0022])
2维tensor进行softmax例子代码实现如下:
import torch
import torch.nn.functional as F
if __name__ == '__main__':
data=torch.rand(2,3)
print(data)
y=F.softmax(data,dim=1)
# dim=0,就是在1维上进行softmax,也就是在列上进行
# dim=1,就是在2维上进行softmax,也就是在行上进行
print(y)
输出结果
tensor([[0.1899, 0.3969, 0.8333],
[0.9149, 0.8438, 0.4973]])
tensor([[0.2420, 0.2976, 0.4604],
[0.3861, 0.3596, 0.2543]])

