浪在ACM新春大作战
题目链接:
| # | Name | 补题状态 |
|---|---|---|
| A |
已补
|
|
| B |
已补
|
|
| C |
已补
|
|
| D | ||
| E |
A:Memory and Crow
There are n integers b1, b2, ..., bn written in a row. For all i from 1 to n, values ai are defined by the crows performing the following procedure:
- The crow sets ai initially 0.
- The crow then adds bi to ai, subtracts bi + 1, adds the bi + 2 number, and so on until the n'th number. Thus, ai = bi - bi + 1 + bi + 2 - bi + 3....
Memory gives you the values a1, a2, ..., an, and he now wants you to find the initial numbers b1, b2, ..., bn written in the row? Can you do it?
Input
The first line of the input contains a single integer n (2 ≤ n ≤ 100 000) — the number of integers written in the row.
The next line contains n, the i'th of which is ai ( - 109 ≤ ai ≤ 109) — the value of the i'th number.
Output
Print n integers corresponding to the sequence b1, b2, ..., bn. It's guaranteed that the answer is unique and fits in 32-bit integer type.
Examples
5
6 -4 8 -2 3
2 4 6 1 3
5
3 -2 -1 5 6
1 -3 4 11 6
Note
In the first sample test, the crows report the numbers 6, - 4, 8, - 2, and 3 when he starts at indices 1, 2, 3, 4 and 5 respectively. It is easy to check that the sequence 2 4 6 1 3 satisfies the reports. For example, 6 = 2 - 4 + 6 - 1 + 3, and - 4 = 4 - 6 + 1 - 3.
In the second sample test, the sequence 1, - 3, 4, 11, 6 satisfies the reports. For example, 5 = 11 - 6 and 6 = 6.
题意描述:
大致意思就是,输入n输入n个整数,求挨着的两个整数和,然后最后一个整数单独输出。//因博主没过四级:题意是看样例看出来的,具体不确定
#include<iostream>
#include<algorithm>
#include<string>
#include<math.h>
using namespace std;
#define ll long long
int main() {
ll n, a[100010];
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
if (i > 0)cout << a[i] + a[i - 1] << " ";
}
cout << a[n - 1] << "\n";
return 0;
}
B. Memory and Trident
Memory is performing a walk on the two-dimensional plane, starting at the origin. He is given a string s with his directions for motion:
- An 'L' indicates he should move one unit left.
- An 'R' indicates he should move one unit right.
- A 'U' indicates he should move one unit up.
- A 'D' indicates he should move one unit down.
But now Memory wants to end at the origin. To do this, he has a special trident. This trident can replace any character in s with any of 'L', 'R', 'U', or 'D'. However, because he doesn't want to wear out the trident, he wants to make the minimum number of edits possible. Please tell Memory what is the minimum number of changes he needs to make to produce a string that, when walked, will end at the origin, or if there is no such string.
Input
The first and only line contains the string s (1 ≤ |s| ≤ 100 000) — the instructions Memory is given.
Output
If there is a string satisfying the conditions, output a single integer — the minimum number of edits required. In case it's not possible to change the sequence in such a way that it will bring Memory to to the origin, output -1.
Examples
RRU
-1
UDUR
1
RUUR
2
Note
In the first sample test, Memory is told to walk right, then right, then up. It is easy to see that it is impossible to edit these instructions to form a valid walk.
In the second sample test, Memory is told to walk up, then down, then up, then right. One possible solution is to change s to "LDUR". This string uses 1 edit, which is the minimum possible. It also ends at the origin.
题目大意:
输入一串字符串,包含:U(上),D(下),L(左),R(右),你在原点,按照字符串走,然后你可以随意修改里边任意一个字符改成你想要的,求最少修改多少次可以走回到原点,会不到的话输出-1。
1 》如果字符串长度是奇数的话肯定走不回原点。
2 》一个D就能抵消一个U,一个L就能抵消一个R,求抵消后的 sum= abs(sl - sr) + abs(su - sd),向右走一个,只需要修改第二个向左走就行,上下同理,所以结果为sum/2
#include<iostream>
#include<algorithm>
#include<string>
#include<math.h>
using namespace std;
int main() {
string a;
int sl = 0, sr = 0, su = 0, sd = 0, sum = 0;
//sl:'L'个数 sr:'R'个数 su:'U'个数 sd:'D'个数
cin >> a;
if (a.size() & 1)cout << "-1\n";
else {
for (int i = 0; i < a.size(); i++) {
if (a[i] == 'L')sl++;
else if (a[i] == 'R')sr++;
else if (a[i] == 'U')su++;
else sd++;
}
sum = abs(sl - sr) + abs(su - sd);
cout << sum / 2 << "\n";
}
return 0;
}
C. Memory and De-Evolution
Memory is now interested in the de-evolution of objects, specifically triangles. He starts with an equilateral triangle of side length x, and he wishes to perform operations to obtain an equilateral triangle of side length y.
In a single second, he can modify the length of a single side of the current triangle such that it remains a non-degenerate triangle (triangle of positive area). At any moment of time, the length of each side should be integer.
What is the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y?
Input
The first and only line contains two integers x and y (3 ≤ y < x ≤ 100 000) — the starting and ending equilateral triangle side lengths respectively.
Output
Print a single integer — the minimum number of seconds required for Memory to obtain the equilateral triangle of side length y if he starts with the equilateral triangle of side length x.
Examples
6 3
4
8 5
3
22 4
6
Note
In the first sample test, Memory starts with an equilateral triangle of side length 6 and wants one of side length 3. Denote a triangle with sides a, b, and c as (a, b, c). Then, Memory can do 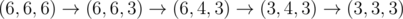 .
.
In the second sample test, Memory can do 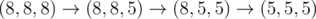 .
.
In the third sample test, Memory can do: 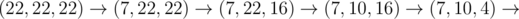
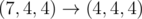 .
.
题目大意:
将一个长度为x的等边三角形变化成长度为y的等边三角形,一次只能改一条边,并且改完后仍然满足三条边构成三角形。(x>=y)
长变短,和短变长修改次数一样,所以逆向模拟,每次最多能把 最短的一条边 改成 两条长边-1,三条边都大于x,即满足条件。逆向推的好处是能够满足三角形的约束下改变最大。
例:3=>6 (3.3.5),(3.5.7),(5.7.11),(7.11.17)
#include<iostream>
#include<algorithm>
#include<string>
#include<math.h>
using namespace std;
#define ll long long
int main() {
int x, y,cnt=0;//cnt:修改次数
cin >> x >> y;
int a[3], b;
a[0]=a[1]=a[2]= y;
b= x;
while (a[0] < x || a[1] < x || a[2] < x) {//有一条边小于x,就不满足条件
sort(a, a + 3);
a[0] = a[1] + a[2] - 1;
cnt++;
}
cout << cnt << "\n";
return 0;
}

