正态分布与平方损失

正态分布和线性回归之间的关系很密切。 正态分布也称为高斯分布， 最早由德国数学家高斯（Gauss）应用于天文学研究。 简单的说若随机变量\(x\)具有均值\(\mu\)和方差\(\sigma^2\)（标准差\(\sigma\)），其正态分布概率密度函数如下：

\[p(x)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\dfrac{1}{2\sigma^2}\left(x-\mu\right)^2\right) \]

正态分布可视化如下：

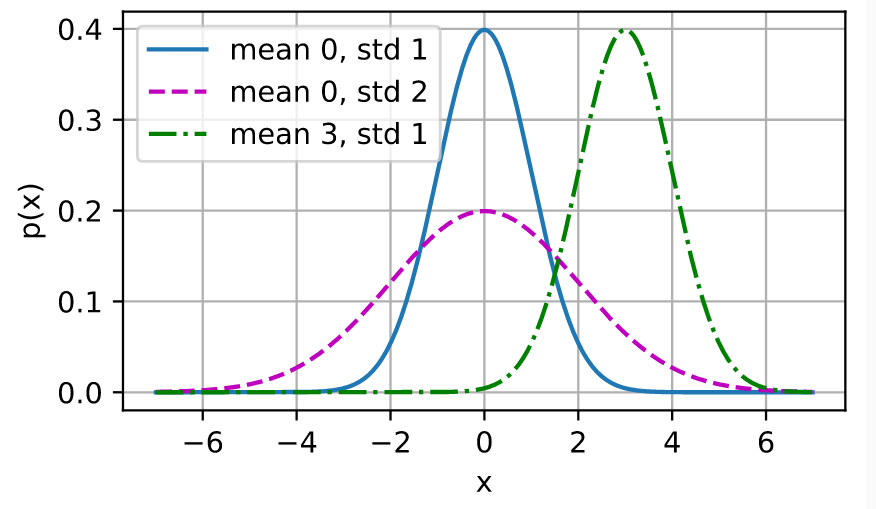
就像我们所看到的，改变均值会产生沿\(x\)轴的偏移，增加方差将会分散分布、降低其峰值。

均方误差损失函数（简称均方损失）可以用于线性回归的一个原因是： 我们假设了观测中包含噪声，其中噪声服从正态分布。 噪声正态分布如下式:

\[y = \mathbf{w}^\top \mathbf{x} + b + \epsilon \]

其中：\(\epsilon \sim \mathcal{N}(0, \sigma^2)\)

因此，我们现在可以写出通过给定的\(\mathbf{x}\)观测到特定\(y\)的似然：

\[P(y \mid \mathbf{x}) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp\left(-\frac{1}{2 \sigma^2} (y - \mathbf{w}^\top \mathbf{x} - b)^2\right). \]

现在，根据极大似然估计法，参数\(\mathbf{w}\)和\(b\)的最优值是使整个数据集的似然最大的值：

\[P(\mathbf y \mid \mathbf X) = \prod_{i=1}^{n} p(y^{(i)}|\mathbf{x}^{(i)}). \]

根据极大似然估计法选择的估计量称为极大似然估计量。 虽然使许多指数函数的乘积最大化看起来很困难， 但是我们可以在不改变目标的前提下，通过最大化似然对数来简化。 由于历史原因，优化通常是说最小化而不是最大化。 我们可以改为最小化负对数似\(-\log P(\mathbf y \mid \mathbf X)\)。 由此可以得到的数学公式是：

\[-\log P(\mathbf y \mid \mathbf X) = \sum_{i=1}^n \frac{1}{2} \log(2 \pi \sigma^2) + \frac{1}{2 \sigma^2} \left(y^{(i)} - \mathbf{w}^\top \mathbf{x}^{(i)} - b\right)^2. \]

现在我们只需要假设\(\sigma\)是某个固定常数就可以忽略第一项， 因为第一项不依赖于\(\mathbf{w}\)和\(b\)。 现在第二项除了常数\(\frac{1}{\sigma^2}\)外，其余部分和前面介绍的均方误差是一样的。 幸运的是，上面式子的解并不依赖于\(\sigma\)。 因此，在高斯噪声的假设下，最小化均方误差等价于对线性模型的极大似然估计。