机器学*中的交叉熵

信息量

一件事发生的概率越*，其蕴含的信息量就越少，反之，若发生的几率越小，则蕴含的信息量就越*。例如，“太阳从东方升起”：这件事发生概率极*，*家都*以为常，所以不觉得有什么不妥的地方，因此蕴含信息量很小。但“国足踢入世界杯”：这就蕴含的信息量很*了，因为这件事的发生概率很小。若某事$x$的发生概率为$P(x)$，则信息量的计算公式为：

$$I(x)=-\log (P(x))$$

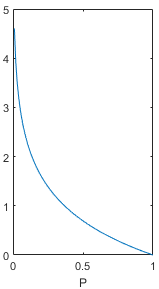
其中，log表示自然对数，底数为$e$（也有资料使用底数为2的对数）。公式中，$P(x)$值落在0到1之间，画出上面函数在$P$为$0-1$时的取值，图像如下。在概率值$P$趋向于0时，信息量趋向于正无穷，在概率值$P$趋向于1时，信息量趋向于0，这个函数能够满足信息量的基本想法。

信息熵

信息熵又称熵，熵可以表达数据的信息量*小。其本质是所有信息量的期望。期望是试验中每次可能结果的概率乘以其结果的总和。熵的公式如下：

$$H(\mathbf{X})=-\sum_{i=1}^{n} P\left(x_{i}\right) \log \left(P\left(x_{i}\right)\right) \quad\left(\mathbf{X}=x_{1}, x_{2}, x_{3} \ldots, x_{n}\right)$$

相对熵（KL散度）

如果我们对于同一个随机变量 $x$有两个单独的概率分布 $P(x)$ 和 $Q(x)$，我们可以使用 KL 散度来衡量这两个分布的差异。相对熵的基本定义是：如果用$P$来描述目标问题，而不是用$Q$来描述目标问题，得到的信息增量。

在机器学*中，$P$往往用来表示样本的真实分布，$Q$用来表示模型所预测的分布，我们训练的目的就是让 $P(x)$ 和 $Q(x)$的差异越来越小。

KL散度的计算公式如下：

$$D_{KL}(P||Q)=\sum\limits_{i=1}^nP(x_i)\log(\dfrac{P(x_i)}{Q(x_i)})$$

其中$n$为事件的所有可能性。$D_{KL}$的值越小，表示$Q$分布和$P$分布越接近.

交叉熵

我们分解相对熵的公式：

$$\begin{aligned} D_{K L}(P \| Q) & =\sum_{i=1}^n P\left(x_i\right) \log \left(P\left(x_i\right)\right)-\sum_{i=1}^n P\left(x_i\right) \log \left(Q\left(x_i\right)\right) \\ & =-H(P(x))+\left[-\sum_{i=1}^n P\left(x_i\right) \log \left(Q\left(x_i\right)\right)\right] \end{aligned}$$

$H(X)$为之前的信息熵，后面那一坨其实就是交叉熵了，所以可以看到：KL散度 = 交叉熵 - 信息熵。

所以交叉熵的公式如下：

$$H\left(P,Q\right)=-\sum\limits_{i=1}^{n}P\left(x_{i}\right)\log\left(Q\left(x_{i}\right)\right)$$

从信息熵的公式我们知道，对于同一个数据集，其信息熵是不变的，所以信息熵可以看作一个常数，因此当KL散度最小时，也即是交叉熵最小时。所以在多分类任务中，KL散度(相对熵)和交叉熵是等价的，我们也就可以用交叉熵来当作损失函数。