直方图变换
直方图和累计直方图
直方图公式如下:
其中\(n_k\)为图像中灰度级为\(r\)的像素个数。累计直方图公式如下:
直方图的归一化表示方式为:
其中\(MN\)为总像素个数。
直方图均衡化
直方图均衡化主要用于增强动态范围(像素最大值和最小值之间的的范围)偏小图像的对比度(图像中明暗区域最亮的白和最暗的黑之间不同亮度层级的测量),做法就是把图像的直方图变换为均匀分布的形式。变换效果如下:
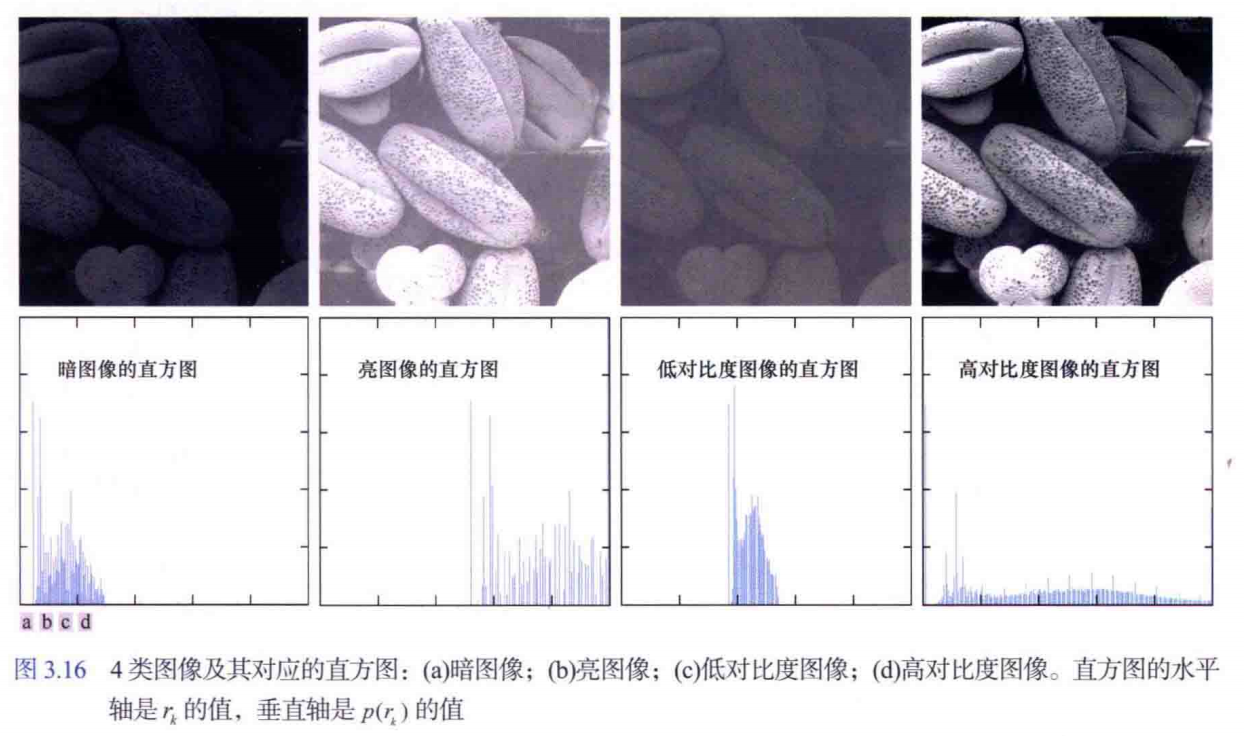
假设直方图均衡化对应的灰度变换函数为:
则此变换满足下面三个条件:
- \(T(r)\) 在区间 \(0 \leq r \leq L-1\)上是一个严格单调递增函数。(严格单调是为了可以进行反变换)
- 对于 \(0 \leq r \leq L-1\) , 有 \(0 \leq T(r) \leq L-1\)。
- \(T(r)\) 可以把\(r\)的分布转化为\(s\)的均匀分布。
下面我们就来寻找此变换函数,先考虑连续的函数。
图像的灰度可视为区间 \([0, L-1]\) 内的一个随机变量。令 \(p_{r}(r)\) 和 \(p_{s}(s)\) 表示两幅不同图像中灰度值 \(r\) 和 \(s\) 的 \(PDF\)(概率密度函数 )。 \(p\) 的下标表明 \(p_{r}\) 和 \(p_{s}\) 是不同的函数。概率论的一个基本结论是,若已知 \(p_{r}(r)\) 和 \(T(r)\) , 且 \(T(r)\) 是连续的且在感兴趣的值域上是可微的, 则变换 (映射) 后的变量 \(s\) 的 \(PDF\) 是:
我们考虑如下变换公式:
式中, 右侧的积分是随机变量 \(r\) 的累积分布函数 (\(CDF\))。由于 \(PDF\) 总为正, 且函数的积分是函数下方的面积, 因此可以证明上式所示的变换函数满足条件1。这是因为函数下方的面积在 \(r\) 增大时并不减小。当这个公式中的上限是 \(r=L-1\) 时, 积分结果为 1 。因此, \(s\) 的最大值为 \(L-1\) , 所以也满足条件2。
由前式可得:
所以:
由于最终得到的\(p_{s}(s)\)是一个均匀分布得概率密度,所以\(s=T(r)=(L-1) \int_{0}^{r} p_{r}(w) \mathrm{d} w\)函数满足条件三,即它就是我们要找的直方图均衡化对应的灰度变换函数。(在离散的情况下,得到的结果往往并不是严格的均匀分布,但问题不大)
直方图均衡化实战
假设一幅大小为 \(64 \times 64\) 像素 (\(M N=4096\) ) 的 3 比特图像 \((L=8)\) 具有下表中的灰度分布, 其中灰度级是区间 \([0, L-1]=[0,7]\) 内的整数。这幅图像的直方图如下图(a)所示。
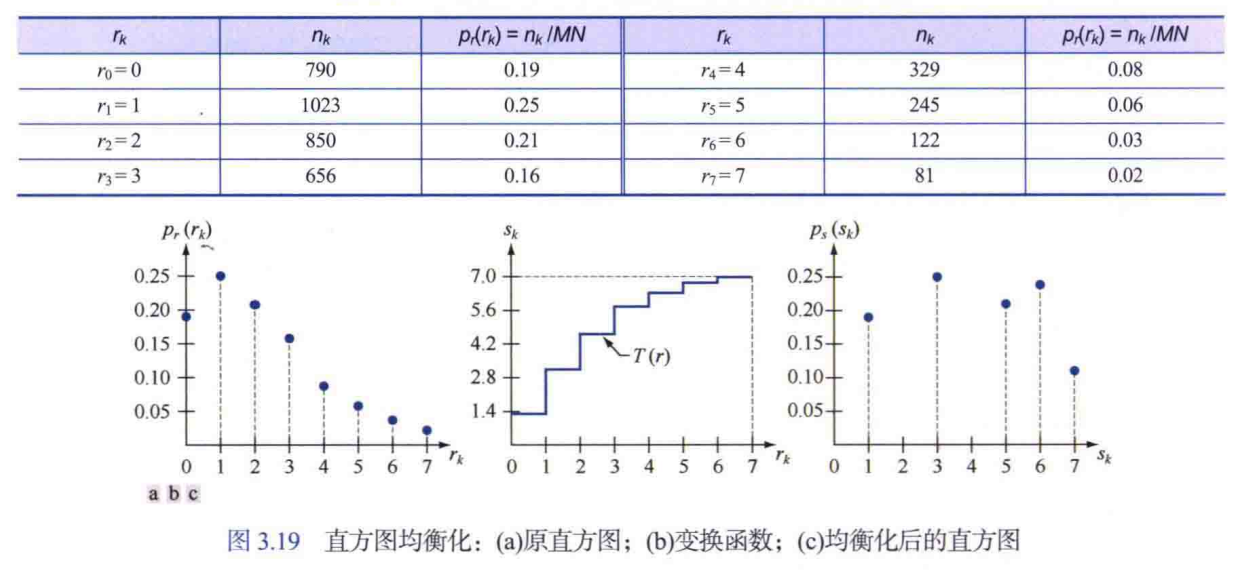
利用直方图均衡化变换函数进行变换,如:
并将得到的结果四舍五入取整,最终得到:
根据此灰度映射,便可以得到均衡化后的图像。
直方图规定化
直方图均衡化输出的图像具有均匀的直方图,但是有时候我们需要生成具有特定直方图的图像,这就是直方图规定化。在理解了直方图均衡化的基础上,直方图规定化就很简单,主要有三个步骤:
- 对原图像进行直方图均衡化,得到一个灰度变换函数\(s=T(r)\).
- 对于规定的直方图,我们同样也能得到一个使它均衡化的灰度变换函数\(s=G(z)\).
- 将2中得到的变换函数的反函数应用于1中的变换函数,即:\(z=G^{-1}(T(r))\),这就是我们需要的最终的变换函数。
(我们假设\(s\)为具有均匀分布的某图像的灰度)
一般来说,求解\(G^{-1}\)的解析表达式并不容易,但在离散的情况下很容易处理,我们可以遍历所有可能的取值计算出一张由输入到输出的映射表,然后存储起来,根据输出来查找输入值即可。
(欢迎转载,转载请注明出处。文中如有错误,还请指出。)



