图像灰度映射

常见的灰度映射

图像反转

假设图像像素值范围为\([0,L-1]\),则反转变换函数为：

\[s=L-1-r \]

实例如下：

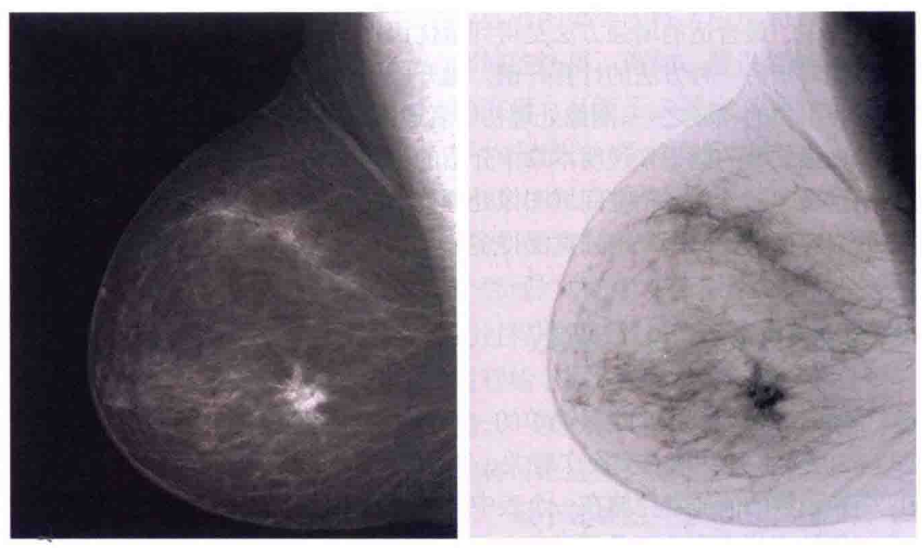
对数变换

对数变换公式为：

\[s=c \log (1+r) \]

这个变换将输入中较窄的低灰度值转换为范围较宽的灰度级，反对数（指数）变换效果相反。

指数（伽马）变换

指数变换公式为：

\[S=c r^{\gamma} \]

对应的图像：

可以看出，对于不同的伽马值，变换效果不同。伽马值小于1时，作用类似于对数变换；伽马值等于1时，是恒等变换。

实例：

分段线性变换

对比度拉伸

光照不足、成像传感器的动态范围偏小、图像获取过程中镜头孔径的设置错误等, 都可能产生低对比度图像。对比度拉伸可以扩展图像中的灰度级范围, 使其覆盖记录介质或显示设备的整个理想灰度范围。实例如下：

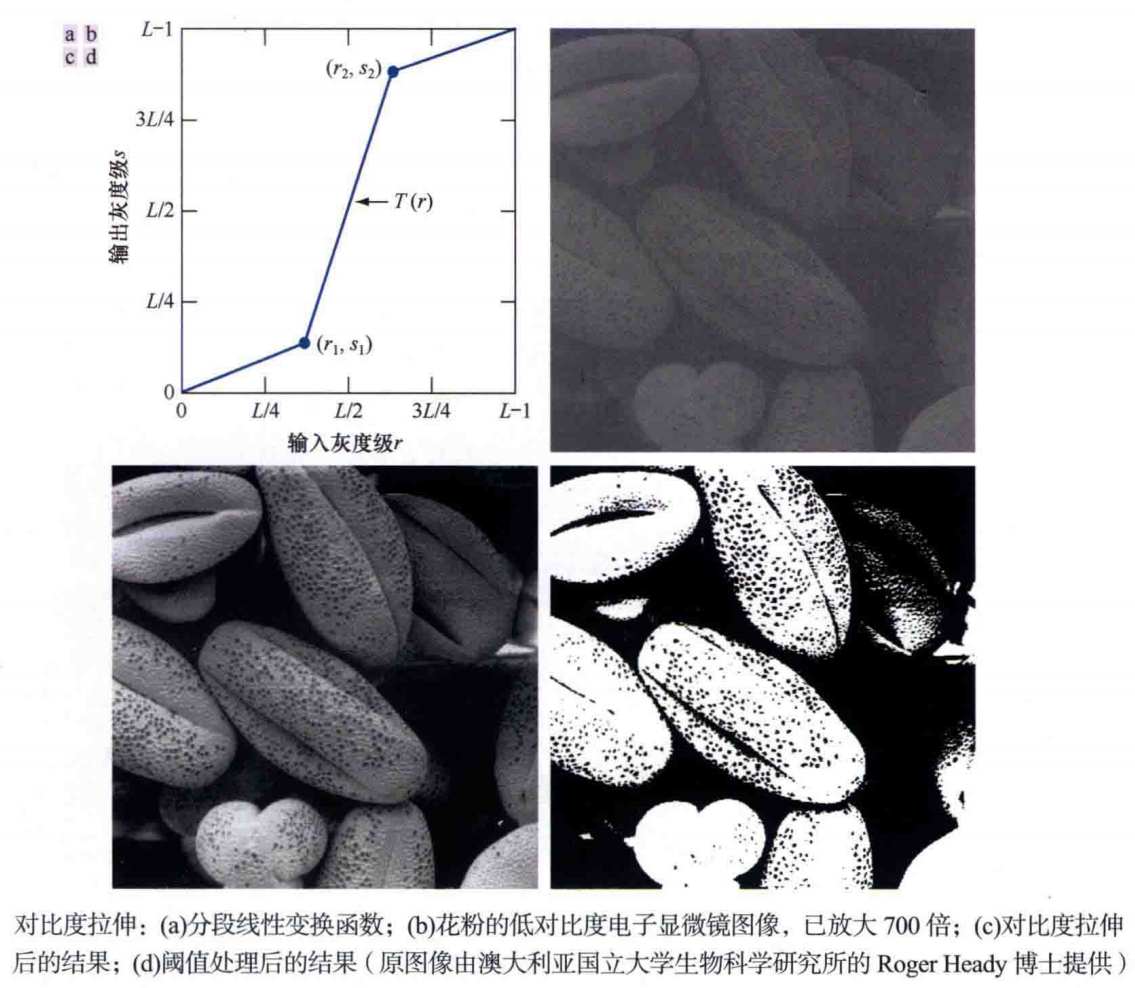
灰度级分层

有些应用的目的是突出图像中的特定灰度区间, 这样的应用包括增强卫星图像中的特征（如水体)、增强 \(\mathrm{X}\) 射线图像中的缺陷等。这种称为灰度级分层的方法可用几种方法实现, 但多数方法都是两个基本方法的变体。一种方法是将感兴趣范围内的所有灰度值显示为一个值 (如白色), 而将所有其他灰度值显示为另一个值 (如黑色)。这种变换产生一幅二值图像。另一种方法是使期望的灰度范围变亮 (或变暗), 但保持图像中的其他灰度级不变。函数图像如下：

比特面分层

将图像分解成各个比特平面对我们分析图像中每个比特的相对重要性是有用的, 这个过程有助于确定量化图像所用比特数的充分性。此外, 这种分解对图像压缩而言也是有用的, 此时所用的平面数量要少于重建图像时所用的平面数量（但会损失一些精度）。如下图：