前馈神经网络
神经元
一个神经元的结构如下:
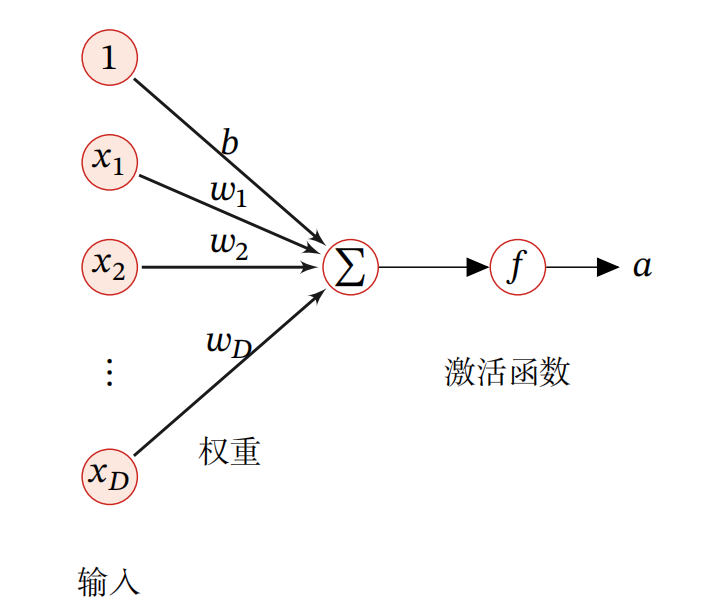
用数学公式表示为:
激活函数
激活函数在神经元中非常重要的.为了增强网络的表示能力和学习能力,激活函数需要具备以下几点性质:
(1) 连续并可导(允许少数点上不可导)的非线性函数.可导的激活函数可以直接利用数值优化的方法来学习网络参数.
(2) 激活函数及其导函数要尽可能的简单,有利于提高网络计算效率.
(3) 激活函数的导函数的值域要在一个合适的区间内,不能太大也不能太小,否则会影响训练的效率和稳定性.
下面介绍几种在神经网络中常用的激活函数.
Sigmoid型函数
Sigmoid 型函数是指一类 S 型曲线函数,为两端饱和函数.
Logistic函数
因为Logistic函数的性质,使得装备了Logistic激活函数的神经元具有以下两点性质:1)其输出直接可以看作概率分布,使得神经网络可以更好地和统计学习模型进行结合.2)其可以看作一个软性门(Soft Gate),用来控制其他神经元输出信息的数量.
Tanh函数
Tanh 函数的输出是零中心化的,而 Logistic 函数的输出恒大于 0. 非零中心化的输出会使得其后一层的神经元的输入发生偏置偏移,并进一步使得梯度下降的收敛速度变慢.
以上两个函数的图像为:
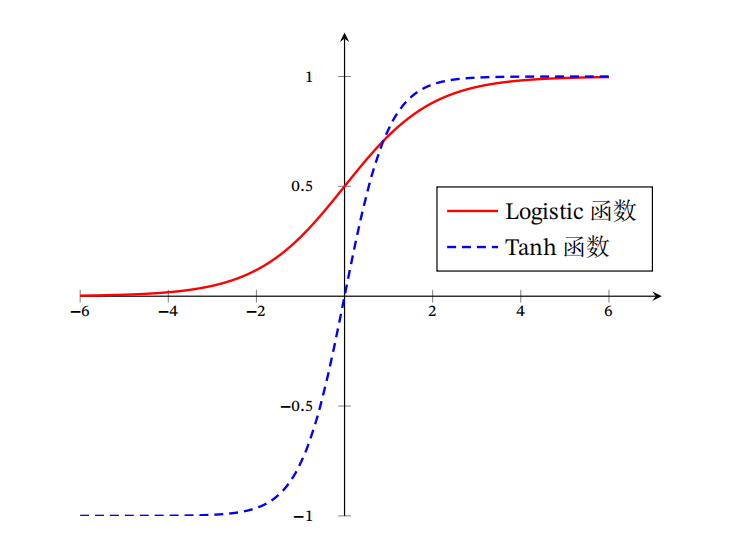
Logistic函数和Tanh函数都是Sigmoid型函数,具有饱和性,但是计算开销较大.因为这两个函数都是在中间(0附近)近似线性,两端饱和.因此,这两个函数可以通过分段函数来近似.
Hard-Logistic函数和Hard-Tanh函数
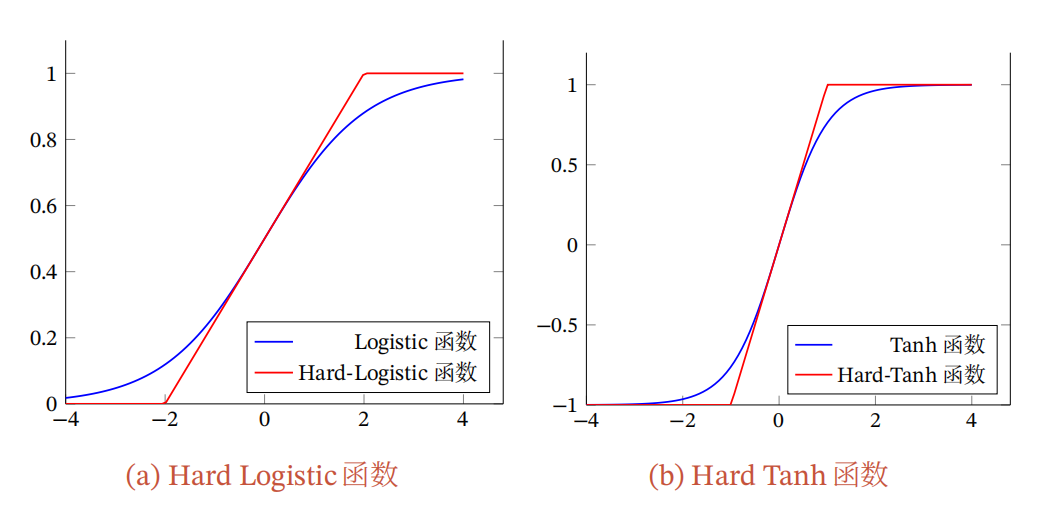
ReLU函数
ReLU
目前深度神经网络中经常使用的激活函数.采用 ReLU 的神经元只需要进行加、乘和比较的操作,计算上更加高效.
ReLU 函数的输出是非零中心化的,给后一层的神经网络引入偏置偏移,会影响梯度下降的效率.此外,ReLU 神经元在训练时比较容易“死亡”.在训练时,如果参数在一次不恰当的更新后,第一个隐藏层中的某个 ReLU 神经元在所有的训练数据上都不能被激活,那么这个神经元自身参数的梯度永远都会是0,在以后的训练过程中永远不能被激活.这种现象称为死亡 ReLU 问题,并且也有可能会发生在其他隐藏层.
带泄露的ReLU
带泄露的ReLU(Leaky ReLU)在输入 𝑥 < 0时,保持一个很小的梯度𝛾.这样当神经元非激活时也能有一个非零的梯度可以更新参数,避免永远不能被激活.带泄露的ReLU的定义如下:
其中 𝛾是一个很小的常数,比如0.01.当𝛾 < 1时,带泄露的ReLU也可以写为:
相当于是一个比较简单的maxout单元.
带参数的ReLU
带参数的 ReLU(Parametric ReLU,PReLU)引入一个可学习的参数,不同神经元可以有不同的参数.对于第 𝑖 个神经元,其 PReLU 定义为:
PReLU 可以允许不同神经元具有不同的参数,也可以一组神经元共享一个参数.
ELU函数
ELU(Exponential Linear Unit,指数线性单元)是一个近似的零中心化的非线性函数,其定义为:
其中 𝛾 ≥ 0是一个超参数,决定𝑥 ≤ 0时的饱和曲线,并调整输出均值在0附近.
Softplus函数
Softplus 函数可以看作 Rectifier 函数的平滑版本,其定义为:
Softplus函数其导数刚好是Logistic函数.Softplus函数虽然也具有单侧抑制、宽兴奋边界的特性,却没有稀疏激活性.
以上函数的图形如下:
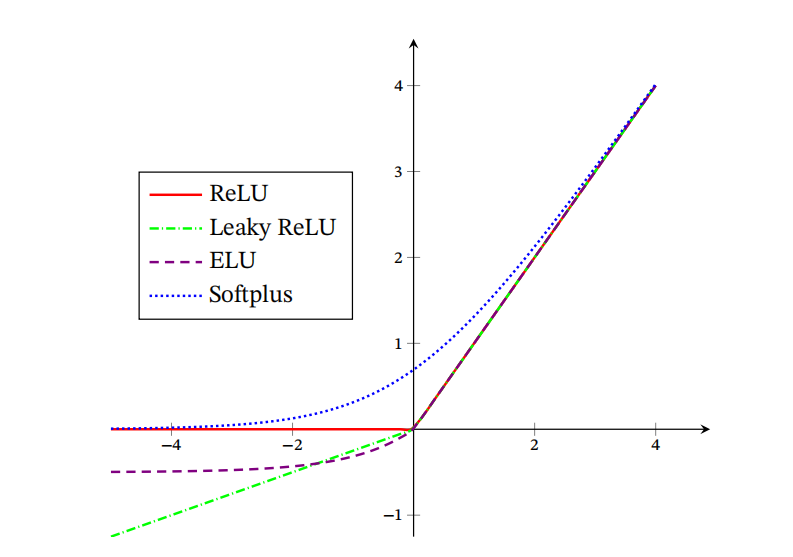
Swish函数
Swish 函数是一种自门控(Self-Gated)激活函数,定义为:
其中 𝜎(⋅) 为 Logistic 函数,可以看作一种软性的门控机制.𝛽 为可学习的参数或一个固定超参数.𝜎(⋅) ∈ (0, 1) 当𝜎(𝛽𝑥)接近于1时,门处于“开”状态,激活函数的输出近似于𝑥 本身;当𝜎(𝛽𝑥)接近于0时,门的状态为“关”,激活函数的输出近似于0.
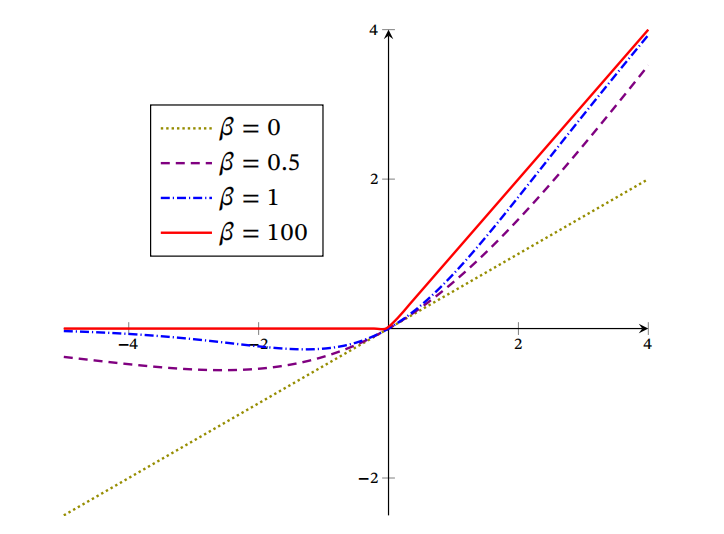
Swish函数可以看作线性函数和ReLU函数之间的非线性插值函数,其程度由参数𝛽 控制.
GELU函数
GELU(Gaussian Error Linear Unit,高斯误差线性单元)也是一种通过门控机制来调整其输出值的激活函数,和 Swish 函数比较类似.
其中𝑃(𝑋 ≤ 𝑥)是高斯分布𝒩(𝜇, 𝜎2)的累积分布函数,其中𝜇, 𝜎为超参数,一般设𝜇 = 0, 𝜎 = 1即可.由于高斯分布的累积分布函数为S型数,因此GELU函数可以用Tanh函数或Logistic函数来近似.
Maxout单元
我们假设网络某一层的输入特征向量为:\(\mathrm{x}=\left(\mathrm{x}_{1}, \mathrm{x}_{2}, \cdots, \mathrm{x}_{\mathrm{d}}\right)\),也就是我们输入是d个神经元。Maxout函数的输出如下:
前馈神经网络
在前馈神经网络中,各神经元分别属于不同的层.每一层的神经元可以接收前一层神经元的信号,并产生信号输出到下一层.第0层称为输入层,最后一层称为输出层,其他中间层称为隐藏层.整个网络中无反馈,信号从输入层向输出层单向传播,可用一个有向无环图示.
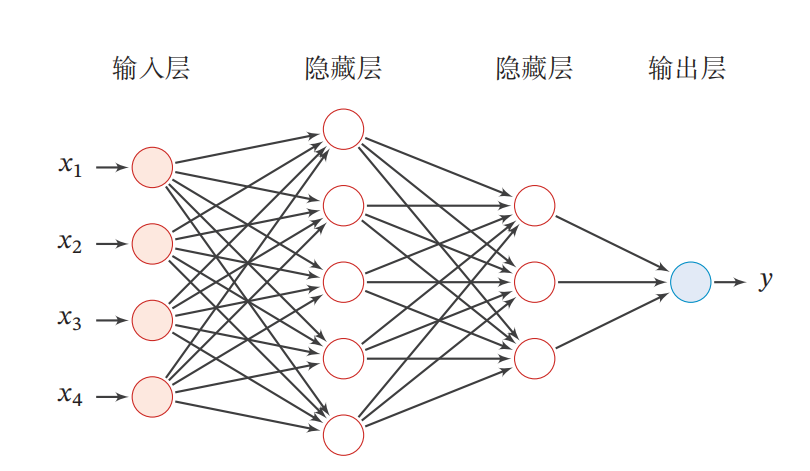
在用数学公式表达神经网络的运算过程前,我们先规定一些前馈神经网络记号:
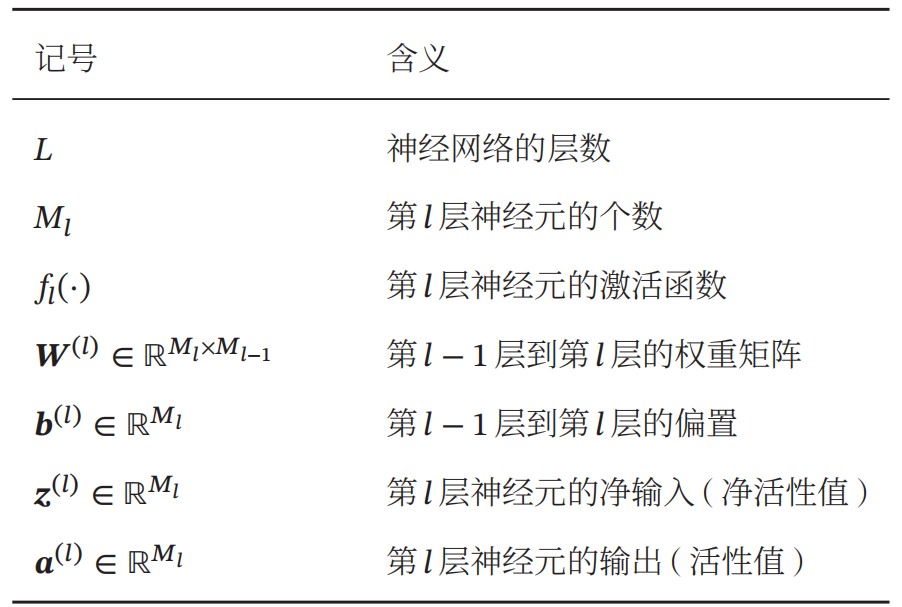
令 \(\boldsymbol{a}^{(0)}=\boldsymbol{x}\) ,前馈神经网络通过不断迭代下面公式进行信息传播:
这样,前馈神经网络可以通过逐层的信息传递,得到网络最后的输出 \(a^{(L)}\) .
(欢迎转载,转载请注明出处。文中如有错误,还请指出。)



