图像的坐标变换

图像的坐标变换

图像的平移、旋转、缩放等都属于图像的坐标的变换。图像中的每一个像素都有一个坐标，比如某像素的坐标是$v=(x,y)$,则像素的坐标变换可以写成矩阵的乘积形式：

$$v'=Av$$

其中$A$是一个$2\times 2$的变换矩阵。对与有$m$个像素的图像，他们的坐标组成了一个$2 \times m$的矩阵$V$，则关于图像的坐标变换为：

$$V'=AV$$

但是在使用中，我们并不直接使用2维的像素坐标，而是它的齐次坐标形式，下面就对齐次坐标做一个说明。

齐次坐标

齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示，是指一个用于投影几何里的坐标系统。

在齐次坐标里，需要三个值来表示投影平面上的一点。则点 $(\mathrm{X}, \mathrm{Y})$ 在齐次坐标里面变成了 $(\mathrm{x}, \mathrm{y}, \mathrm{w})$ ，并且有 $\mathrm{X}=\mathrm{x} / \mathrm{w}$, $\mathrm{Y}=\mathrm{y} / \mathrm{w}$ 。笛卡尔坐标系下 $(1,2)$ 的齐次坐标可以表示为 $(1,2,1)$ ，如果点 $(1,2)$ 移动到无限远 处，在笛卡尔坐标下它变为 $(\infty, \infty)$ ，然后它的齐次坐标表示为 $(1,2,0)$ ，因为 $\left(\frac{1}{0}, \frac{2}{0}\right)=(\infty, \infty)$ ，我们可以不用 $\infty$ 来表示一个无穷远处的点。下面为齐次坐标与笛卡尔坐标的转换关系。

$$\begin{array}{l} (x,y,w) <=>\left(\frac{x}{w}, \frac{y}{w}\right)=(X,Y) \\ (1,2,1) <=>\left(\frac{1}{1}, \frac{2}{1}\right)=(1,2) \\ (2,4,2) <=>\left(\frac{2}{2}, \frac{4}{2}\right)=(1,2) \end{array}$$

齐次坐标在电脑图形内无处不在，因为该坐标允许平移、旋转、缩放及透视投影等可表示为矩阵与向量相乘的一般向量运算。依据链式法则，任何此类运算的序列均可相乘为单一个矩阵，从而实现简单且有效之处理。与此相反，若使用笛卡儿坐标，平移及透视投影不能表示成矩阵相乘。所以接下来我们用齐次坐标来表示图形的坐标变换。

仿射变换

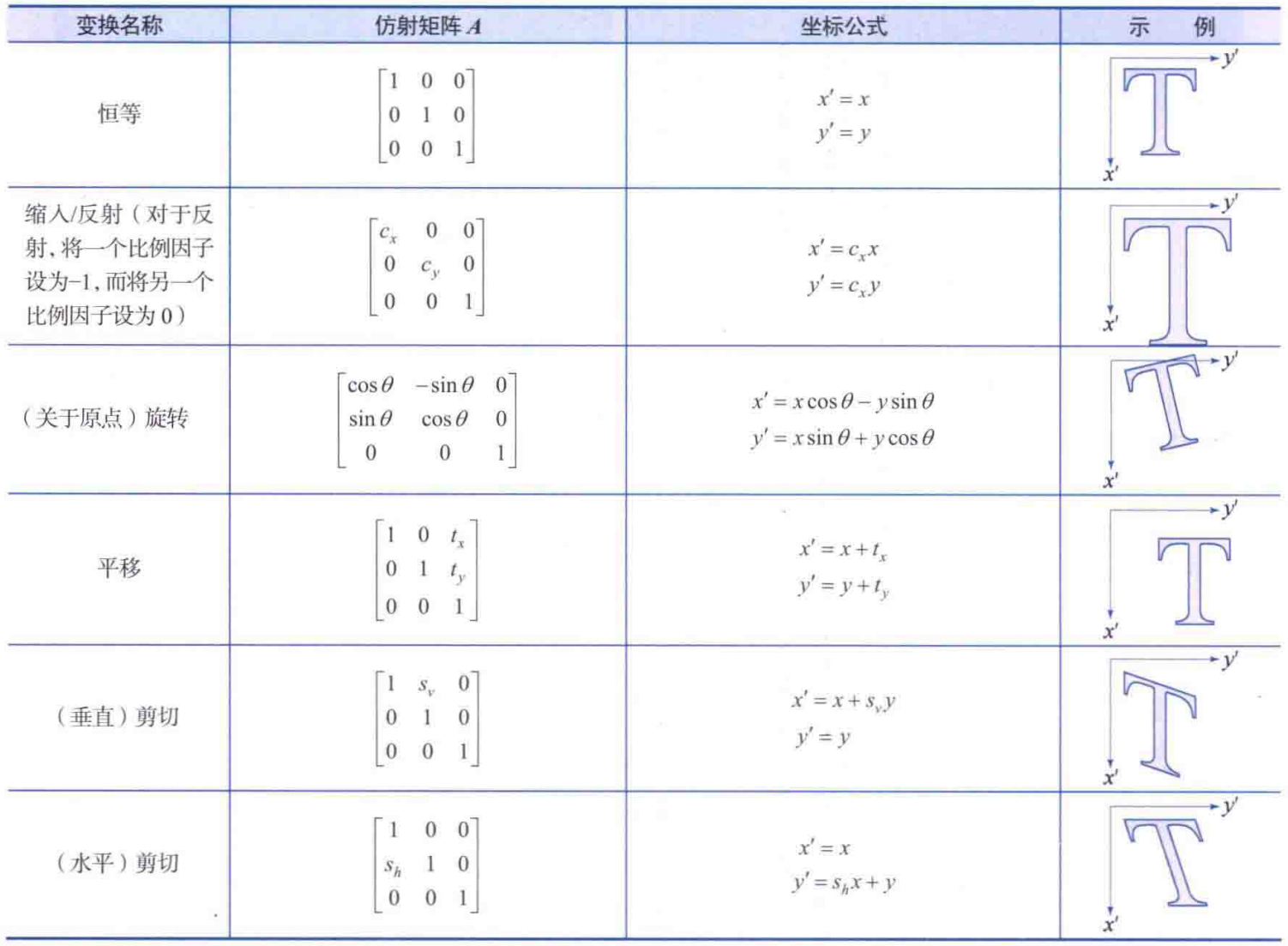
仿射变换就是线性变换加平移，线性变换有三个特点：

1. 变换前是直线，变换后依然是直线；
2. 直线比例保持不变
3. 变换前是原点，变换后依然是原点

旋转变换的分解

一个旋转变换可以看作是两个剪切变换的结合：

$$\boldsymbol{R}=\left[\begin{array}{ccc} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} 1 & 0 & 0 \\ -\tan \theta & 1 / \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos \theta & \sin \theta & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$$

示意图如下：

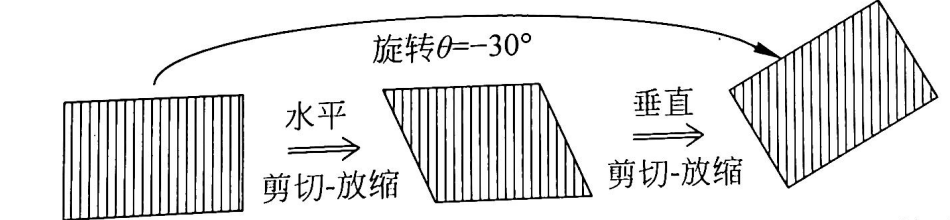
第一个变换为：

$$\begin{array}{c} x^{\prime}=x \cos \theta+y \sin \theta \\ y^{\prime}=y \end{array}$$

即图像被用偏移量 $y \sin \theta$ 水平平移, 并根据因子$x \cos \theta$ 而收缩 。

第二个变换为：

$$\begin{array}{l} x^{\prime \prime}=x^{\prime} \\ y^{\prime \prime}=y^{\prime} / \cos \theta-x^{\prime} \tan \theta \end{array}$$

它仅在垂直方向进行剪切和收缩变换。

为了避免使用收缩变换，也可以使用三个剪切变换来组合：

$$\boldsymbol{R}=\left[\begin{array}{ccc} \cos \theta & \sin \theta & 0 \\ -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right]=\left[\begin{array}{ccc} 1 & \tan (\theta / 2) & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & 0 & 0 \\ -\sin \theta & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} 1 & \tan (\theta / 2) & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]$$