NOIP模板总结
模板总结
数据结构
单调队列
int main(void)
{
n=read(),k=read();
for(int i=1;i<=n;++i)a[i]=read();
for(int i=1;i<=n;++i)
{
while(l<r&&q[l]<i-k+1)l++;
while(l<r&&a[q[r-1]]>a[i])r--;
q[r++]=i;
if(i>=k)printf("%d ",a[q[l]]);
}
putchar('\n');
l=r=0;
for(int i=1;i<=n;++i)
{
while(l<r&&q[l]<i-k+1)l++;
while(l<r&&a[q[r-1]]<a[i])r--;
q[r++]=i;
if(i>=k)printf("%d ",a[q[l]]);
}
return 0;
}
单调栈
stack<int>s;
int main(void)
{
n=read();
for(int i=1;i<=n;++i)hig[i]=read();
for(int i=1;i<=n;++i)
{
if(s.empty())s.push(hig[i]);
else if(hig[i]>=s.top())
{
while(!s.empty()&&hig[i]>=s.top())s.pop();
if(!s.empty())ans+=s.size();
s.push(hig[i]);
}
else
{
if(!s.empty())ans+=s.size();
s.push(hig[i]);
}
}
printf("%d\n",ans);
return 0;
}
树状数组
单点修改，区间查询
class BIT
{
private:
int sum[maxn];
public:
inline void modify(int x,int val) {for(int i=x;i<=n;i+=(i&-i)) sum[i]+=val;}
inline int query(int x) {int res=0;for(int i=x;i;i-=(i&-i)) res+=sum[i];return res;}
}bit;
区间修改，区间查询
class BIT
{
private:
int sum1[maxn],sum2[maxn];
public:
inline void add(int x,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
sum1[i]+=val,sum2[i]+=val*(x-1);
}
inline int sum(int x)
{
int ans=0;
for(int i=x;i>0;i-=lowbit(i))
ans+=sum1[i]*x-sum2[i];
return ans;
}
}bit;
线段树
区间修改，区间加
struct SegmentTree
{
ll sum[maxn<<2],tag[maxn<<2];
void update(int u,int l,int r,ll k) {tag[u]+=k;sum[u]+=(ll)(r-l+1)*k;}
void pushdown(int u,int l,int r,int mid)
{
if(!tag[u]) return;
update(u<<1,l,mid,tag[u]);
update(u<<1|1,mid+1,r,tag[u]);
tag[u]=0;
}
void modify(int u,int l,int r,int x,int y,ll k)
{
if(x<=l&&r<=y) return update(u,l,r,k);
int mid=(l+r)>>1;
pushdown(u,l,r,mid);
if(x<=mid) modify(u<<1,l,mid,x,y,k);
if(y>mid)modify(u<<1|1,mid+1,r,x,y,k);
sum[u]=sum[u<<1]+sum[u<<1|1];
}
ll query(int u,int l,int r,int x,int y)
{
if(x<=l&&r<=y) return sum[u];
int mid=(l+r)>>1;ll res=0;
pushdown(u,l,r,mid);
if(x<=mid) res+=query(u<<1,l,mid,x,y);
if(y>mid) res+=query(u<<1|1,mid+1,r,x,y);
return res;
}
void build(int u,int l,int r)
{
if(l==r) return sum[u]=a[l],void();
int mid=(l+r)>>1;
build(u<<1,l,mid);
build(u<<1|1,mid+1,r);
sum[u]=sum[u<<1]+sum[u<<1|1];
}
}seg;
区间修改，区间加乘
struct Node
{
ll sum,add,mul;
}tr[maxn*4];
ll a[maxn],mod;
int n,m;
void build(int u,int l,int r)
{
tr[u].mul=1;tr[u].add=0;
if(l==r) return tr[u].sum=a[l],void();
int mid=(l+r)>>1;
build(u<<1,l,mid);build(u<<1|1,mid+1,r);
tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%mod;
}
inline void update(int u,int len,ll add,ll mul)
{
tr[u].mul=tr[u].mul*mul%mod;
tr[u].add=(tr[u].add*mul+add)%mod;
tr[u].sum=(tr[u].sum*mul+add*len)%mod;
}
inline void pushdown(int u,int l,int r,int mid)
{
if(tr[u].add==0&&tr[u].mul==1) return;
update(u<<1,mid-l+1,tr[u].add,tr[u].mul);
update(u<<1|1,r-mid,tr[u].add,tr[u].mul);
tr[u].add=0;tr[u].mul=1;
}
void modify_add(int u,int l,int r,int x,int y,ll val)
{
if(x<=l&&r<=y) return update(u,r-l+1,val,1);
int mid=(l+r)>>1;
pushdown(u,l,r,mid);
if(mid>=x) modify_add(u<<1,l,mid,x,y,val);
if(y>mid) modify_add(u<<1|1,mid+1,r,x,y,val);
tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%mod;
}
void modify_mul(int u,int l,int r,int x,int y,ll val)
{
if(x<=l&&r<=y) return update(u,r-l+1,0,val);
int mid=(l+r)>>1;
pushdown(u,l,r,mid);
if(mid>=x) modify_mul(u<<1,l,mid,x,y,val);
if(y>mid) modify_mul(u<<1|1,mid+1,r,x,y,val);
tr[u].sum=(tr[u<<1].sum+tr[u<<1|1].sum)%mod;
}
ll query(int u,int l,int r,int x,int y)
{
if(x<=l&&r<=y) return tr[u].sum;
int mid=(l+r)>>1;
ll res=0;
pushdown(u,l,r,mid);
if(x<=mid) res=(res+query(u<<1,l,mid,x,y))%mod;
if(y>mid) res=(res+query(u<<1|1,mid+1,r,x,y))%mod;
return res;
}
线段树维护区间最值与区间历史最值
给出一个长度为 \(n\) 的数列 \(A\)，同时定义一个辅助数组 \(B\)，\(B\) 开始与 \(A\) 完全相同。接下来进行了 \(m\) 次操作，操作有五种类型，按以下格式给出：
1 l r k：对于所有的 \(i\in[l,r]\)，将 \(A_i\) 加上 \(k\)（\(k\) 可以为负数）。2 l r v：对于所有的 \(i\in[l,r]\)，将 \(A_i\)变成 \(\min(A_i,v)\)。3 l r：求 \(\sum_{i=l}^{r}A_i\)。4 l r：对于所有的 \(i\in[l,r]\)，求 \(A_i\) 的最大值。5 l r：对于所有的 \(i\in[l,r]\)，求 \(B_i\) 的最大值。
在每一次操作后，我们都进行一次更新，让 \(B_i\gets\max(B_i,A_i)\)。
struct Node
{
int l,r,mid,mx,hmx,nmx,cnt,add1,hadd1,add2,hadd2;
ll sum;
}tr[maxn<<2];
int a[maxn],n;
inline void pushup(int u)
{
tr[u].sum=tr[u<<1].sum+tr[u<<1|1].sum;
tr[u].hmx=max(tr[u<<1].hmx,tr[u<<1|1].hmx);
if(tr[u<<1].mx==tr[u<<1|1].mx)
{
tr[u].mx=tr[u<<1].mx;
tr[u].nmx=max(tr[u<<1].nmx,tr[u<<1|1].nmx);
tr[u].cnt=tr[u<<1].cnt+tr[u<<1|1].cnt;
}
else if(tr[u<<1].mx>tr[u<<1|1].mx)
{
tr[u].mx=tr[u<<1].mx;
tr[u].nmx=max(tr[u<<1].nmx,tr[u<<1|1].mx);
tr[u].cnt=tr[u<<1].cnt;
}
else
{
tr[u].mx=tr[u<<1|1].mx;
tr[u].nmx=max(tr[u<<1|1].nmx,tr[u<<1].mx);
tr[u].cnt=tr[u<<1|1].cnt;
}
}
inline void update(int u,int k1,int hk1,int k2,int hk2)
{
tr[u].sum+=1ll*k1*tr[u].cnt+1ll*k2*(tr[u].r-tr[u].l+1-tr[u].cnt);
tr[u].hmx=max(tr[u].hmx,tr[u].mx+hk1);
tr[u].hadd1=max(tr[u].hadd1,tr[u].add1+hk1);
tr[u].mx+=k1,tr[u].add1+=k1;
tr[u].hadd2=max(tr[u].hadd2,tr[u].add2+hk2);
if(tr[u].nmx!=-inf) tr[u].nmx+=k2;
tr[u].add2+=k2;
}
inline void pushdown(int u)
{
if(!tr[u].add1&&!tr[u].add2&&!tr[u].hadd1&&!tr[u].hadd2) return;
int tmx=max(tr[u<<1].mx,tr[u<<1|1].mx);
if(tr[u<<1].mx==tmx) update(u<<1,tr[u].add1,tr[u].hadd1,tr[u].add2,tr[u].hadd2);
else update(u<<1,tr[u].add2,tr[u].hadd2,tr[u].add2,tr[u].hadd2);
if(tr[u<<1|1].mx==tmx) update(u<<1|1,tr[u].add1,tr[u].hadd1,tr[u].add2,tr[u].hadd2);
else update(u<<1|1,tr[u].add2,tr[u].hadd2,tr[u].add2,tr[u].hadd2);
tr[u].add1=tr[u].hadd1=tr[u].add2=tr[u].hadd2=0;
}
void build(int u,int l,int r)
{
tr[u].l=l,tr[u].r=r;
if(l==r)
{
tr[u].mid=l;
tr[u].sum=tr[u].mx=tr[u].hmx=a[l];
tr[u].nmx=-inf;tr[u].cnt=1;return;
}
int mid=(l+r)>>1;tr[u].mid=mid;
build(u<<1,l,mid);build(u<<1|1,mid+1,r);
pushup(u);
}
void modifyadd(int u,int x,int y,int val)
{
if(x<=tr[u].l&&tr[u].r<=y) {update(u,val,val,val,val);return;}
pushdown(u);
if(x<=tr[u].mid) modifyadd(u<<1,x,y,val);
if(y>tr[u].mid) modifyadd(u<<1|1,x,y,val);
pushup(u);
}
void modifymv(int u,int x,int y,int val)
{
if(val>=tr[u].mx) return;
if(x<=tr[u].l&&tr[u].r<=y&&val>tr[u].nmx)
{update(u,val-tr[u].mx,val-tr[u].mx,0,0);return;}
pushdown(u);
if(x<=tr[u].mid&&tr[u<<1].mx>val) modifymv(u<<1,x,y,val);
if(y>tr[u].mid&&tr[u<<1|1].mx>val) modifymv(u<<1|1,x,y,val);
pushup(u);
}
ll querysum(int u,int x,int y)
{
if(x<=tr[u].l&&tr[u].r<=y) return tr[u].sum;
pushdown(u);
ll res=0;
if(x<=tr[u].mid) res+=querysum(u<<1,x,y);
if(y>tr[u].mid) res+=querysum(u<<1|1,x,y);
return res;
}
int querymx(int u,int x,int y)
{
if(x<=tr[u].l&&tr[u].r<=y) return tr[u].mx;
pushdown(u);
int ans=-inf;
if(x<=tr[u].mid) ans=max(ans,querymx(u<<1,x,y));
if(y>tr[u].mid) ans=max(ans,querymx(u<<1|1,x,y));
return ans;
}
int queryhmx(int u,int x,int y)
{
if(x<=tr[u].l&&tr[u].r<=y) return tr[u].hmx;
pushdown(u);
int ans=-inf;
if(x<=tr[u].mid) ans=max(ans,queryhmx(u<<1,x,y));
if(y>tr[u].mid) ans=max(ans,queryhmx(u<<1|1,x,y));
return ans;
}
可持久化线段树 (可持久化数组)
int wife[maxn*24],lc[maxn*24],rc[maxn*24];
int rt[maxn],a[maxn],tot,n,m;
void build(int &u,int l,int r)
{
u=++tot;
if(l==r) return wife[u]=a[l],void();
int mid=(l+r)>>1;
build(lc[u],l,mid);build(rc[u],mid+1,r);
}
void modify(int &u,int pre,int l,int r,int x,int val)
{
u=++tot;lc[u]=lc[pre];rc[u]=rc[pre];
if(l==r) return wife[u]=val;
int mid=(l+r)>>1;
if(x<=mid) modify(lc[u],lc[pre],l,mid,x,val);
else modify(rc[u],rc[pre],mid+1,r,x,val);
}
int query(int u,int l,int r,int x)
{
if(l==r) return wife[u];
int mid=(l+r)>>1;
if(x<=mid) return query(lc[u],l,mid,x);
else return query(rc[u],mid+1,r,x);
}
主席树
int lc[maxn<<5],rc[maxn<<5],sum[maxn<<5],rt[maxn],tot,n,m,q;
void build(int &u,int l,int r)
{
u=++tot;
if(l==r) return;
int mid=(l+r)>>1;
build(lc[u],l,mid);build(rc[u],mid+1,r);
}
void modify(int &u,int pre,int l,int r,int x)
{
u=++tot;lc[u]=lc[pre];rc[u]=rc[pre];sum[u]=sum[pre]+1;
if(l==r) return;
int mid=(l+r)>>1;
if(x<=mid) modify(lc[u],lc[pre],l,mid,x);
else modify(rc[u],rc[pre],mid+1,r,x);
}
int query(int u,int v,int l,int r,int k)
{
if(l==r) return l;
int x=sum[lc[v]]-sum[lc[u]],mid=(l+r)>>1;
if(x>=k) return query(lc[u],lc[v],l,mid,k);
else return query(rc[u],rc[v],mid+1,r,k-x);
}
平衡树
Splay
#include <cstdio>
#include <iostream>
using namespace std;
const int maxn=1e5+5,inf=0x3f3f3f3f;
int siz[maxn],fa[maxn],ch[maxn][2],rep[maxn],vl[maxn];
int n,tot;
inline int ids(int x) {return ch[fa[x]][0]==x?0:1;}
inline void update(int x) {siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+rep[x];}
inline void connect(int x,int f,int fs) {fa[x]=f;ch[f][fs]=x;}
inline void rotate(const int &x)
{
int f=fa[x],ff=fa[fa[x]];
int s1=ids(x),s2=ids(f);
connect(ch[x][s1^1],f,s1);connect(f,x,s1^1);connect(x,ff,s2);
update(f);update(x);
}
inline void splay(int x,int to)
{
while(fa[x]!=to)
{
if(fa[fa[x]]==to) rotate(x);
else if(ids(fa[x])==ids(x)) rotate(fa[x]),rotate(x);
else rotate(x),rotate(x);
}
}
inline int newnode(const int &val,const int &f) {fa[++n]=f;vl[n]=val;siz[n]=rep[n]=1;return n;}
int find(int val)
{
int now=ch[0][0],nxt;
while(1)
{
if(vl[now]==val){
splay(now,0);
return now;
}
nxt=val<vl[now]?0:1;
if(!ch[now][nxt]) return 0;
now=ch[now][nxt];
}
}
void insert(int val)
{
tot++;
if(!ch[0][0]) {ch[0][0]=newnode(val,0);return;}
int now=ch[0][0],nxt;
while(1)
{
siz[now]++;
if(val==vl[now]){
rep[now]++;splay(now,0);return;
}
nxt=val<vl[now]?0:1;
if(!ch[now][nxt])
{
ch[now][nxt]=newnode(val,now);
splay(ch[now][nxt],0);
return;
}
now=ch[now][nxt];
}
}
inline int lowe(int x)
{
int now=ch[0][0],ans=-inf;
while(now){
if(vl[now]<x&&vl[now]>ans) ans=vl[now];
now=ch[now][x>vl[now]?1:0];
}
return ans;
}
inline int uppe(int x)
{
int now=ch[0][0],ans=inf;
while(now){
if(vl[now]>x&&vl[now]<ans) ans=vl[now];
now=ch[now][x<vl[now]?0:1];
}
return ans;
}
void delt(int x)
{
tot--;
int dl=find(x);
if(!dl) return;
if(rep[dl]>1) {siz[dl]--;rep[dl]--;return;}
if(!ch[dl][0]) {connect(ch[dl][1],0,0);return;}
if(!ch[dl][1]) {connect(ch[dl][0],0,0);return;}
int px=ch[dl][0];
while(ch[px][1]) px=ch[px][1];
splay(px,dl);
connect(ch[dl][1],px,1);connect(px,0,0);
update(px);
}
int rk(int val)
{
int ans=0,now=ch[0][0];
while(now)
{
if(vl[now]==val){
ans+=siz[ch[now][0]]+1;break;
}
if(val<vl[now]) now=ch[now][0];
else ans+=siz[ch[now][0]]+rep[now],now=ch[now][1];
}
splay(now,0);
return ans;
}
int rrk(int x)
{
if(x>tot) return -inf;
int now=ch[0][0],tmp;
while(now)
{
tmp=rep[now]+siz[ch[now][0]];
if(siz[ch[now][0]]<x&&x<=tmp) break;
if(x<tmp) now=ch[now][0];
else x-=tmp,now=ch[now][1];
}
splay(now,0);
return vl[now];
}
Fhq_treap
struct Fhq_treep_Node
{
int val,siz,ch[2],rnd;
}tr[maxn];
int rt,r1,r2,r3,utot;
inline void update(const int &u) {tr[u].siz=tr[tr[u].ch[0]].siz+tr[tr[u].ch[1]].siz+1;}
inline int newnode(const int &val) {tr[++utot].val=val;tr[utot].siz=1;tr[utot].rnd=rand();return utot;}
void split(int u,int val,int &a,int &b)
{
if(!u) return a=b=0,void();
if(tr[u].val<=val) a=u,split(tr[a].ch[1],val,tr[a].ch[1],b);
else b=u,split(tr[b].ch[0],val,a,tr[b].ch[0]);
update(u);
}
int merge(int a,int b)
{
if(!a||!b) return a+b;
if(tr[a].rnd<tr[b].rnd)
{
tr[a].ch[1]=merge(tr[a].ch[1],b);
update(a);return a;
}
else
{
tr[b].ch[0]=merge(a,tr[b].ch[0]);
update(b);return b;
}
}
void insert(int val)
{
split(rt,val,r1,r2);
rt=merge(r1,merge(newnode(val),r2));
}
void delt(int val)
{
split(rt,val,r1,r3);
split(r1,val-1,r1,r2);
r2=merge(tr[r2].ch[0],tr[r2].ch[1]);
rt=merge(merge(r1,r2),r3);
}
int rnk(int val)
{
split(rt,val-1,r1,r2);
int ans=tr[r1].siz+1;
rt=merge(r1,r2);
return ans;
}
int kth(int u,int k)
{
while(1)
{
if(tr[tr[u].ch[0]].siz>=k) u=tr[u].ch[0];
else if(k>tr[tr[u].ch[0]].siz+1) k=k-tr[tr[u].ch[0]].siz-1,u=tr[u].ch[1];
else return u;
}
}
void lower(int val)
{
split(rt,val-1,r1,r2);
printf("%d\n",tr[kth(r1,tr[r1].siz)].val);
rt=merge(r1,r2);
}
void upper(int val)
{
split(rt,val,r1,r2);
printf("%d\n",tr[kth(r2,1)].val);
rt=merge(r1,r2);
}
WBLT (leafy_tree)
struct Node
{
int siz,val;
Node *ch[2];
Node(int siz,int val,Node *lc,Node *rc) : siz(siz),val(val) {
this->ch[0]=lc;this->ch[1]=rc;
}
Node(){}
}*rt,*st[maxn*3],*null,tt[maxn*3];
int utot;//,a[maxn];
inline void pushup(Node *u)
{
if(u->ch[0]->siz==0) return;
u->siz=u->ch[0]->siz+u->ch[1]->siz;
u->val=u->ch[1]->val;
}
inline void rotate(Node *u)
{
if(u->ch[0]->siz > u->ch[1]->siz*ratio)
u->ch[1]=merge(u->ch[0]->ch[1],u->ch[1]),st[--utot]=u->ch[0],u->ch[0]=u->ch[0]->ch[0];
else if(u->ch[1]->siz > u->ch[0]->siz*ratio)
u->ch[0]=merge(u->ch[0],u->ch[1]->ch[0]),st[--utot]=u->ch[1],u->ch[1]=u->ch[1]->ch[1];
}
void insert(Node *u,int val)
{
if(u->siz==1)
{
u->ch[0]=newnode(1,min(u->val,val),null,null);
u->ch[1]=newnode(1,max(u->val,val),null,null);
}
else insert(val > u->ch[0]->val?u->ch[1]:u->ch[0],val);
pushup(u);rotate(u);
}
void erase(Node *u,int val)
{
if(u->ch[0]->siz==1&&u->ch[0]->val==val)
st[--utot]=u->ch[0],st[--utot]=u->ch[1],*u=*u->ch[1];
else if(u->ch[1]->siz==1&&u->ch[1]->val==val)
st[--utot]=u->ch[0],st[--utot]=u->ch[1],*u=*u->ch[0];
else erase(val > u->ch[0]->val?u->ch[1]:u->ch[0],val);
pushup(u);rotate(u);
}
int kth(Node *u,int siz)
{
if(u->siz==1) return u->val;
return siz > u->ch[0]->siz ? kth(u->ch[1],siz-u->ch[0]->siz) : kth(u->ch[0],siz);
}
int rnkx(Node *u,int val)
{
if(u->siz==1) return 1;
return val > u->ch[0]->val ? u->ch[0]->siz+rnkx(u->ch[1],val) : rnkx(u->ch[0],val);
}
int pre(int x) {return kth(rt,rnkx(rt,x)-1);}
int suf(int x) {return kth(rt,rnkx(rt,x+1));}
int main()
{
int opt,x,n,m,las=0,tot=0;
read(m);
for(int i=0;i<=maxn*2;++i) st[i]=&tt[i];
null=new Node(0,0,null,null);
rt=new Node(1,2147483647,null,null);
while(m--)
{
read(opt);read(x);
if(opt==1) insert(rt,x);
else if(opt==2) erase(rt,x);
else if(opt==3) printf("%d\n",rnkx(rt,x));
else if(opt==4) printf("%d\n",kth(rt,x));
else if(opt==5) printf("%d\n",pre(x));
else printf("%d\n",suf(x));
}
return 0;
}
二维树状数组
#define lowbit(x) (x&(-(x)))
int sum[maxn+5][maxn+5];
int n,m;
inline void add(int x,int y,int val)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j))
sum[i][j]+=val;
}
inline int sum(int x,int y)
{
int res=0;
for(int i=x;i>0;i-=lowbit(i))
for(int j=y;j>0;j-=lowbit(j))
res+=sum[i][j];
return res;
}
并查集
int find(int x) {return fa[x]==x?x:fa[x]=find(fa[x]);}
void merge(int x,int y)
{
x=find(x);y=find(y);
if(dep[x]>dep[y]) swap(x,y);
fa[x]=y;dep[y]+=(dep[x]==dep[y]);
}
ST表
void preprmq()
{
for(int i=2;i<=n;++i) lg[i]=lg[i>>1]+1;
for(int i=1;(1<<i)<=n;++i)
for(int j=1;j+(1<<i)-1<=n;++j)
st[j][i]=max(st[j][i-1],st[j+(1<<i-1)][i-1]);
}
inline int query(int l,int r)
{
int k=lg[r-l+1]
return max(st[l][k],st[r-(1<<k)+1][k]);
}
LCT (维护路径异或和，单点修改)
struct LCT_Node
{
int val,fa,ch[2],xv,cg;
}tr[maxn];
int n,m;
inline void read(int &x)
{
char c;
while((c=getchar())<'0'||c>'9');
x=c^48;
while((c=getchar())>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48);
}
inline bool isroot(int u) {return !(tr[tr[u].fa].ch[0]==u||tr[tr[u].fa].ch[1]==u);}
inline void reverse(int u) {swap(tr[u].ch[0],tr[u].ch[1]);tr[u].cg^=1;}
inline int ids(int u) {return tr[tr[u].fa].ch[1]==u;}
inline void connect(int u,int f,int k,bool isr) {if(!isr) tr[f].ch[k]=u;tr[u].fa=f;}
inline void update(int u) {tr[u].xv=tr[tr[u].ch[0]].xv^tr[tr[u].ch[1]].xv^tr[u].val;}
inline void pushdown(int u)
{
if(!tr[u].cg) return;
reverse(tr[u].ch[0]);reverse(tr[u].ch[1]);
tr[u].cg=0;
}
void push(int u)
{
if(!isroot(u)) push(tr[u].fa);
pushdown(u);
}
inline void rotate(int u)
{
int f=tr[u].fa,ff=tr[f].fa,s1=ids(u),s2=ids(f),bp=isroot(f);
connect(tr[u].ch[s1^1],f,s1,0);connect(f,u,s1^1,0);connect(u,ff,s2,bp);
update(f);update(u);
}
inline void splay(int u)
{
push(u);
while(!isroot(u))
{
if(isroot(tr[u].fa)) rotate(u);
else if(ids(tr[u].fa)==ids(u)) rotate(tr[u].fa),rotate(u);
else rotate(u),rotate(u);
}
}
void access(int u)
{
for(int y=0;u;u=tr[y=u].fa)
splay(u),tr[u].ch[1]=y,update(u);
}
void makeroot(int u)
{
access(u);splay(u);
reverse(u);
}
int findroot(int u)
{
access(u);splay(u);
while(tr[u].ch[0]) pushdown(u),u=tr[u].ch[0];
splay(u);
return u;
}
void split(int u,int v)
{
makeroot(u);
access(v);splay(v);
}
void link(int u,int v)
{
makeroot(u);
if(findroot(v)!=u) tr[u].fa=v;
}
void cut(int u,int v)
{
makeroot(u);
if(findroot(v)==u&&tr[v].fa==u&&!tr[u].ch[0])
{
tr[v].fa=tr[u].ch[1]=0;
update(u);
}
}
线性基
ll p[maxn];
void insert(ll x)
{
for(int i=60;i>=0;--i)
{
if(!(x>>(1ll*i)&1)) continue;
if(!p[i]) return p[i]=x,void();
x^=p[i];
}
}
字符串
\(hash\)
把字符串有效地转化为一个整数。
单哈希版：
预处理\(1\)到\(n\)的前缀\(hash\)值：
for(int i=1;i<=n;++i)
ha[i]=(ha[i]*base+s[i])%mod;
取子串的\(hash\)值：
return (ha[r]-ha[l-1]*pw[r-l+1]+mod)%mod;
双哈希版：
预处理\(1\)到\(n\)的前缀\(hash\)值：
for(int i=1;i<=lena;i++)
for(int j=0;j<2;j++)
ha[i][j]=(ha[i-1][j]*base[j]+s[i])%mod[j];
取子串的\(hash\)值：
return make_pair((ha[r][0]-ha[l-1][0]*pw[r-l+1][0]+mod[0])%mod[0]
,(ha[r][1]-ha[l-1][1]*pw[r-l+1][1]+mod[1])%mod[1]);
自然上溢哈希：用\(unsigned\ int\)或\(unsigned\ long\ long\)。
\(hash\)素数的选择：
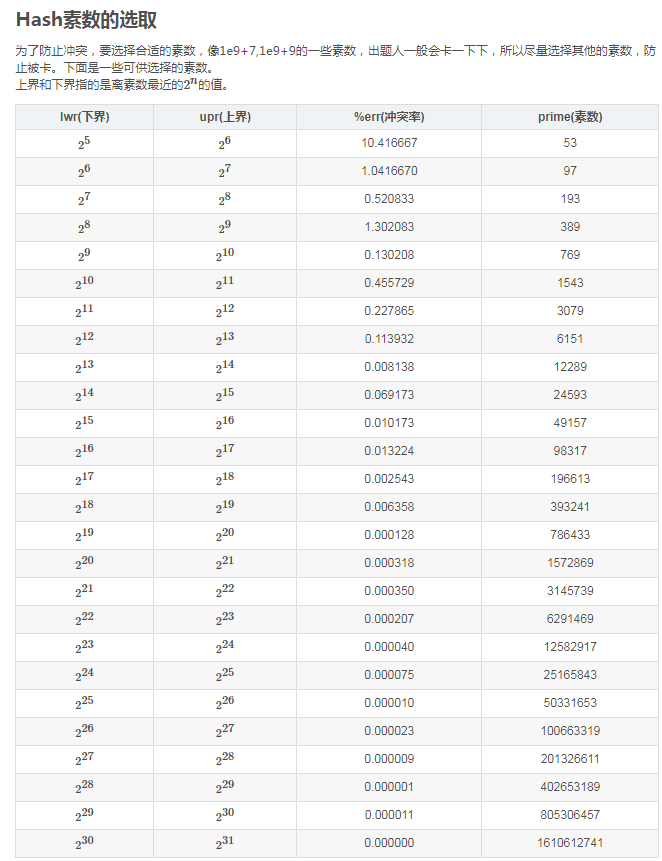
可以参考，也可以选择自己喜欢的质数。
\(Kmp\)
模板（下标从\(0\)开始）：
void Get_next()
{
int i=0,j;
next[0]=j=-1;
while(i<len2)
{
if(j==-1||b[i]==b[j])
next[++i]=++j;
else j=next[j];
}
}
void Kmp()
{
int i=0,j=0;
while(i<len1)
{
if(j==-1||a[i]==b[j])
++i,++j;
else j=next[j];
if(j==len2)
{
printf("%d\n",i-len2+1);
j=next[j];
}
}
}
时间复杂度\(\Theta(|S_1|+|S_2|)\)
\(next\)数组的意义：
- 失配后的下一个匹配位置。
- 前缀的最长的\(border\)。
\(border\)：定义一个字符串\(s\)的\(border\)为\(s\)的一个非\(s\)本身的子串\(t\)，满足\(t\)既是\(s\)的前缀，又是\(s\)的后缀，即前缀后缀最大值。
注：如果下标从一开始，用\(next\)表示\(border\)长度的时候要减一。
应用：最小循环节： len-nxt[len];
扩展\(Kmp\)
给定母串S，和子串T。
定义\(n=|S|,m=|T|,extend[i]=S[i..n]\)与T的最长公共前缀长度。请在线性的时间复杂度内，求出所有的\(extend[1..n]\)。
\(next\)数组意义：\(next[i]\)表示\(T[i..m]\)与\(T\)的最长公共前缀长度。
参考代码（下标从0开始）：
void get_next()
{
int a=0,p=0;
nxt[0]=lent;
for(int i=1;i<lent;i++)
{
if(i+nxt[i-a]<p) nxt[i]=nxt[i-a];
else
{
if(i>=p) p=i;
while(p<lent&&t[p]==t[p-i]) p++;
nxt[i]=p-i;
a=i;
}
}
}
void get_extend()
{
int a=0,p=0;
for(int i=0;i<lens;i++)
{
if(i+nxt[i-a]<p) extend[i]=nxt[i-a];
else
{
if(i>=p) p=i;
while(p<lens&&s[p]==t[p-i]) p++;
extend[i]=p-i;
a=i;
}
}
}
时间复杂度\(\Theta(|S|+|T|)\)
\(Manacher\)
代码：
string s,a;
cin>>s;
a="$~";
int len=s.length();
for(int i=0;i<len;i++)
a+=s[i],a+="~";
int len2=a.length();
vector<int> p(len2+5,0);
int maxr=0,pos=0;
int ans=0;
for(int i=1;i<len2;i++)
{
p[i]= i<maxr ? min(p[2*pos-i],maxr-i) : 1;
while(a[i-p[i]]==a[i+p[i]]) p[i]++;
if(p[i]+i>maxr) maxr=p[i]+i,pos=i;
ans=max(ans,p[i]);
}
时间复杂度\(\Theta(n)\)
\(Trie\)
模板代码（下标从一开始）：
void insert(char *a) //插入
{
int len=strlen(a),u=1;
for(int i=0;i<len;i++)
{
int c=a[i]-'a';
if(!tr[u][c]) tr[u][c]=++tot;
u=tr[u][c];++siz[u]; //siz表示子树中有几个串
}
book[u]=1;
++word[u]; //word表示当前点有几个字符串
}
int find(char *a) //查询a是否存在
{
int len=strlen(a),u=1;
for(int i=0;i<len;i++)
{
int c=a[i]-'a';
if(!tr[u][c]) return 0;
u=tr[u][c];
}
if(!book[u]) return 0;
return 1;
}
void query(int u,int k) //查询字典序第k大，存到s数组中
{
if(word[u]>=k) return;
k-=word[u];
for(int c=0;c<26;++c)
if(tr[u][c])
{
if(k<=siz[tr[u][c]])
return s[++top]=c+'a',query(tr[u][c],k),void();
else k-=siz[tr[u][c]];
}
}
时间复杂度\(\Theta(\sum|S|)\)
\(01\text{Trie}\)处理异或
void insert(int x) //插入
{
int u=1; //注意根节点没有记录siz
for(int i=lim;~i;--i)
{
int s=x>>i&1;
if(!tr[u][s]) tr[u][s]=++cnt;
u=tr[u][s];++siz[u];
}
}
int query(int u,int v,int x) //找异或最大值
{
int res=0;
for(int i=lim;~i;--i)
{
int s=x>>i&1;
if(tr[u][s^1]) res|=(1<<i),u=tr[u][s^1];
else u=tr[u][s];
}
return res;
}
可持久化版本
void insert(int &now,int v,char *s) //插入
{
now=++cnt;int u=now,len=strlen(s+1);
memcpy(tr[u],tr[v],sizeof(tr[v]));
for(int i=1;i<=len;++i)
{
int c=s[i]-'a';
tr[u][c]=++cnt;u=tr[u][c];v=tr[v][c];
siz[u]=siz[v]+1;word[u]=word[v];
memcpy(tr[u],tr[v],sizeof(tr[v]));
}
++word[u];
}
//其他操作与普通版本几乎无区别
\(AC\)自动机
计算\(fail\)指针:
void Getfail() //fail指针
{
queue<int> que;
for(int i=0;i<26;i++)
if(tr[0][i]) que.push(tr[0][i]);
while(!que.empty())
{
int u=que.front();que.pop();
for(int i=0;i<26;i++)
{
int &v=tr[u][i];
if(v) fail[v]=tr[fail[u]][i],que.push(v);
else v=tr[fail[u]][i];
}
}
}
模板\(1\)（下文的变量意义与\(Trie\)中的基本一样）：
给定\(n\)个模式串\(s_i\)和一个文本串\(t\)，求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。
代码：
void query(string s)
{
int u=0,ans=0,len=s.length();
for(int i=0;i<len;i++)
{
u=tr[u][s[i]-'a'];
for(int j=u;j&&word[j]!=-1;j=fail[j])
{
ans+=word[j];
word[j]=-1; //只找一遍
}
}
cout<<ans<<endl;
}
模板\(2\)：
有\(N\)个由小写字母组成的模式串以及一个文本串\(T\)。每个模式串可能会在文本串中出现多次。你需要找出哪些模式串在文本串\(T\)中出现的次数最多。
代码：
void query(string s)
{
int u=0,ans=-1,len=s.length();
for(int i=0;i<len;i++)
{
u=tr[u][s[i]-'a'];
for(int j=u;j;j=fail[j])
vis[word[j]]++; //这里word的意义是该点对应串的编号
}
for(int i=1;i<=n;i++) ans=max(ans,vis[i]);
cout<<ans<<endl;
for(int i=1;i<=n;i++)、
if(vis[i]==ans) cout<<ss[i]<<endl;
}
模板\(3\)：
给你一个文本串\(S\)和\(n\)个模式串\(T_{1..n}\)，请你分别求出每个模式串\(T_i\)在\(S\)中出现的次数。
数据不保证任意两个模式串不相同。
代码（拓扑排序）：
for(int i=0;i<len;i++)
{
int &v=tr[u][s[i]-'a'];
u=v?v:v=++tot;
}
if(!idx[u]) idx[u]=id; //在插入完后记一下每个点在原串中对应的id
else fa[id]=idx[u]; //如果有一个点对应多个id，就像并查集一样连一个fa
//记得fa要初始化为fa[i]=i
int &v=tr[u][i];
if(v) fail[v]=tr[fail[u]][i],que.push(v),++deg[fail[v]]; //在这里记录入度
else v=tr[fail[u]][i];
void query(string s)
{
queue<int> que;
int len=s.length(),u=0;
for(int i=0;i<len;i++)
vis[u=tr[u][s[i]-'a']]++;
//在fail树上跑拓扑排序
for(int i=1;i<=tot;i++)
if(!deg[i]) que.push(i);
while(!que.empty())
{
u=que.front();que.pop();
ans[idx[u]]=vis[u];
vis[fail[u]]+=vis[u]; //fail树上答案向上传递
deg[fail[u]]--;
if(!deg[fail[u]]) que.push(fail[u]);
}
}
后缀数组
void rsort()
{
for(int i=0;i<=m;++i) tax[i]=0;
for(int i=1;i<=n;++i) ++tax[rnk[i]];
for(int i=1;i<=m;++i) tax[i]+=tax[i-1];
for(int i=n;i>0;--i) sa[tax[rnk[tp[i]]]--]=tp[i];
}
void ssort()
{
rsort();
for(int w=1,p;p<n;m=p,w<<=1)
{
p=0;
for(int i=1;i<=w;++i) tp[++p]=n-w+i;
for(int i=1;i<=n;++i) if(sa[i]>w) tp[++p]=sa[i]-w;
rsort();
swap(tp,rnk);
rnk[sa[1]]=p=1;
for(int i=2;i<=n;++i)
rnk[sa[i]]=tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+w]==tp[sa[i-1]+w]?p:++p;
}
}
void Get_height() //height[i]=lcp(i,i-1)，两个后缀的lcp为一段区间height的rmq
{
int p=0,j;
for(int i=1;i<=n;++i)
{
if(p) --p;
j=sa[rnk[i]-1];
while(a[i+p]==a[j+p]) ++p;
height[rnk[i]]=p;
}
}
后缀自动机
\(SAM\)模板
class SAM
{
private:
int link[maxn<<1],tr[maxn<<1][26];
int maxlen[maxn<<1],siz[maxn<<1],a[maxn<<1],las=1,cnt=1;
public:
void insert(int c)
{
int u=las,nu=las=++cnt;
siz[nu]=1;maxlen[nu]=maxlen[u]+1;
for(;u&&!tr[u][c];u=link[u]) tr[u][c]=nu;
if(!u) return link[nu]=1,void();
int v=tr[u][c];
if(maxlen[v]==maxlen[u]+1) return link[nu]=v,void();
int nv=++cnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=link[nu]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
}
void rsort(int x) //通常需要一遍基数排序求拓扑序
{
memset(tax,0,sizeof(tax));
for(int i=1;i<=cnt;++i) ++tax[maxlen[i]];
for(int i=1;i<=x;++i) tax[i]+=tax[i-1];
for(int i=cnt;i;--i) a[tax[maxlen[i]]--]=i;
}
};
广义\(SAM\)模板（在线版）（每插入一个串前把\(las\)设为一）：
int insert(int c,int u)
{
if(tr[u][c])
{
int v=tr[u][c];
if(maxlen[u]+1==maxlen[v]) return v;
int nv=++scnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
return nv;
}
int nu=++scnt;
maxlen[nu]=maxlen[u]+1;
for(;u&&!tr[u][c];u=link[u]) tr[u][c]=nu;
if(!u) return link[nu]=1,nu;
int v=tr[u][c];
if(maxlen[u]+1==maxlen[v]) return link[nu]=v,nu;
int nv=++scnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=link[nu]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
return nu;
}
广义\(SAM\)模板（离线版）：
struct Trie
{
int tr[maxn][26],cnt=1;
void insert(char *s)
{
int len=strlen(s+1),u=1;
for(int i=1;i<=len;++i)
{
int c=s[i]-'a';
u=tr[u][c]?tr[u][c]:tr[u][c]=++cnt;
}
}
}tt;
int insert(int c,int u)
{
int nu=++cnt;
maxlen[nu]=maxlen[u]+1;
for(;u&&!tr[u][c];u=link[u]) tr[u][c]=nu;
if(!u) return link[nu]=1,nu;
int v=tr[u][c];
if(maxlen[v]==maxlen[u]+1) return link[nu]=v,nu;
int nv=++cnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=link[nu]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
return nu;
}
void bfs() //bfs建树
{
pos[1]=1;
que.push(1);
while(!que.empty())
{
int u=que.front();que.pop();
for(int i=0;i<26;++i)
if(tt.tr[u][i])
pos[tt.tr[u][i]]=insert(ipos[u]),que.push(tt.tr[u][i]);
}
}
应用：
求多个字符串的本质不同子串个数。
答案为：\(\sum maxlen[i]-maxlen[link[i]]\)
计算每个节点的\(endpos\)大小
注意上文插入的时候记录的\(siz\)，基数排序后把\(siz\)往\(parent\)树上累加，最后每个点的\(siz\)即为\(endpos\)的大小。
for(int i=cnt;i;--i) siz[link[a[i]]]+=siz[a[i]];
DP
LIS
题意：求给定的序列的最长上升子序列。
复杂度：\(\mathcal{O}(nlog\left(n\right))\)
int n,a[cnt],d[cnt];
int main() {
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",a+i);
d[1]=a[1];int len=1;
for(int i=2;i<=n;i++) {
if(d[len]<=a[i]) d[++len]=a[i];
else {
int l=1,r=len,mid;
while(l<r) {
mid=(l+r)>>1;
if(d[mid]>=a[i]) r=mid;
else l=mid+1;
}
d[l]=a[i];
}
}
printf("%d",len);
return 0;
}
背包
01背包
每个物品选或不选
int n,m,v[5000+5],w[5000+5],f[10000+5];
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d",w+i,v+i);
for(int i=1;i<=n;i++)
for(int j=m;j>=w[i];j--)
f[j]=max(f[j],f[j-w[i]]+v[i]);
printf("%d",f[m]);
return 0;
}
完全背包
每个物品可以选无限个
int n,m,v[5000+5],w[5000+5],f[10000+5];
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d%d",w+i,v+i);
for(int i=1;i<=n;i++)
for(int j=w[i];j<=m;j++)
f[j]=max(f[j],f[j-w[i]]+v[i]);
printf("%d",f[m]);
return 0;
}
多重背包（二进制优化）
每个物品有选择的数量限制
将每个物品的限制\(m_i\)拆分成和比它小的二的次幂和余下的数，满足\(\sum_{i=1}^{k}2^i+s=m_i\)，此时使用拆分的数就可以表示出\(0\rightarrow m_i\)的所有数。于是总共拆分成\(\mathcal{O}(nlog\left(n\right))\)个物品。
int M,N,v[MAXN],w[MAXN],m[MAXN],ans,f[200000+5];
int main() {
scanf("%d%d",&N,&M);
for(int i=1;i<=N;i++) {
scanf("%d%d%d",v+i,w+i,m+i);
if(m[i]*v[i]>M)
for(int j=v[i];j<=M;j++)
f[j]=max(f[j],f[j-v[i]]+w[i]);
else {
int num=m[i],res=1;
while(1) {
if(num>res) {
num-=res;
for(int j=M;j>=res*v[i];j--)
f[j]=max(f[j],f[j-res*v[i]]+res*w[i]);
res*=2;
}
else {
res=num;
for(int j=M;j>=res*v[i];j--)
f[j]=max(f[j],f[j-res*v[i]]+res*w[i]);
break;
}
}
}
}
printf("%d",f[M]);
return 0;
}
分组背包
题意：每个物品归属于一个组，每个组内的物品相互冲突。
int n,m,dp[10000],w[10000],c[10000],id[500][500],cnt[10000];
int cnt=-inf;
int main() {
scanf("%d%d",&m,&n);
for(int i=1;i<=n;i++) {
int x;
scanf("%d%d%d",&w[i],&c[i],&x);
cnt=max(cnt,x);
cnt[x]++;
id[x][cnt[x]]=i;
}
for(int i=1;i<=cnt;i++)
for(int j=m;j>=0;j--)
for(int k=1;k<=cnt[i];k++)
if(j>=w[id[i][k]])
dp[j]=max(dp[j],dp[j-w[id[i][k]]]+c[id[i][k]]);
printf("%d\n",dp[m]);
return 0;
}
树型背包（依赖背包）
题意：每个物品可能必须在某个物品选了之后才能选。
将没有依赖的点的父亲设为节点\(0\)。设\(f_{u,i}\)表示以\(u\)为根的子树背包选了\(i\)体积的最大价值。
\(\mathcal{O}\left(nm^2\right)\)版本：
void dfs(int u) {
for(int i=w[u];i<=m;i++)
f[u][i]=v[u];
for(int i=head[u];i;i=e[i].next) {
int v=e[i].v;
dfs(v);
for(int i=m-w[u];i>=0;i--)
for(int j=0;j<=i;j++)
f[u][i+w[u]]=max(f[u][i+w[u]],f[u][i+w[u]-j]+f[v][j]);
}
}
泛化物品优化：\(\mathcal{O\left(nm\right)}\)
void dfs(int u,int m) {
if(m<=0) return;
for(int i=head[u];i;i=e[i].next) {
int v=e[i].v;
for(int j=0;j<=m-W[v];j++) f[v][j]=f[u][j];
dfs(v,m-W[v]);
for(int j=W[v];j<=m;j++)
f[u][j]=max(f[u][j],f[v][j-W[v]]+V[v]);
}
}
int main() {
/* Read in */
dfs(s,m-W[s]);
printf("%d\n",f[s][m-W[s]]+V[s]);
return 0;
}
\(f_{u,i}\)可以理解为在预留及\(u\)其到根节点的路径上的点的空间后，还剩下的空间\(i\)的最大价值。
\(\texttt{dfs}\)序优化：\(\mathcal{O}\left(nm\right)\)
void dfs(int u) {
id[++cnt]=u;size[u]=1;
for(int i=head[u];i;i=e[i].next) {
int v=e[i].v;
pre[v]=pre[u]+W[u];
dfs(v);
size[u]+=size[v];
}
}
void dp() {
for(int i=1;i<=cnt;i++) {
int u=id[i];
for(int j=pre[u];j<=m-W[u];j++) // 选择这个节点
f[i+1][j+W[u]]=max(f[i+1][j+W[u]],f[i][j]+V[u]);
for(int j=pre[u];j<=m;j++) // 不选这个节点
f[i+size[u]][j]=max(f[i+size[u]][j],f[i][j]);
}
}
int main() {
/* Read in */
dfs(s);
dp();
printf("%d\n",f[cnt+1][m]);
return 0;
}
其中\(pre_u\)表示\(u\)的父节点到根的路径的体积之和。
状压DP
例题题意
在 \(N×N\) 的棋盘里面放 \(K\) 个国王，使他们互不攻击，国王能攻击到它上下左右，以及左上左下右上右下八个方向上附近的各一个格子，共 \(8\) 个格子。求共有多少种摆放方案。
一句话解
枚举当前行和上一行的合法状态，通过合法状态转移到下一行
例题代码
int n,m,tot,st[1<<9],num[1<<9];;
ll dp[10][1<<9][100],ans;
signed main(void)
{
n=read(),m=read();
for(int i=0;i<(1<<n);++i)
{
if(i&(i>>1))continue;
st[++tot]=i;
}
for(int i=1;i<=tot;++i)
{
int x=st[i];
for(;x;x=(x&(x-1)))++num[i];
}
for(int i=1;i<=tot;++i)dp[1][i][num[i]]=1;
for(int l=2;l<=n;++l)
for(int i=1;i<=tot;++i)
for(int j=1;j<=tot;++j)
{
if(st[i]&st[j])continue;
if(st[i]&(st[j]>>1)||st[i]&(st[j]<<1))continue;
for(int k=m;k>=num[i];--k)
dp[l][i][k]+=dp[l-1][j][k-num[i]];
}
for(int i=1;i<=tot;i++)ans+=dp[n][i][m];
cout<<ans<<endl;
}
单调队列优化DP
例题题意
制造一把金宝剑需要 \(n\) 种原料，编号为 \(1\) 到 \(n\)，编号为 \(i\) 的原料的坚固值为 \(a_i\)
炼金是很讲究放入原料的顺序的，因此必须按照 \(1,2,3\cdots n\) 的顺序依次将这些原料放入炼金锅。
但是，炼金锅的容量非常有限，它最多只能容纳 \(w\) 个原料。
每放入一个原料之前，都可以从中取出一些原料，数量不能超过 \(s\) 个。
我们定义第 \(i\) 种原料的耐久度为：放入第 \(i\) 种原料时锅内的原料总数 \(\times\ a_i\) ，则宝剑的耐久度为所有原料的耐久度之和，请求出耐久度的最大值。
注：这里的“放入第 \(i\) 种原料时锅内的原料总数包括正在放入锅中的原料
一句话解
之前的情况中只有个数对当前有影响
得出朴素方程后用单调队列优化
例题代码
int n,m,s;
int a[maxn];
ll f[maxn][maxn],ans=-inf;
signed main(void)
{
n=read(),m=read(),s=read();
for(int i=1;i<=n;++i)a[i]=read();
for(int i=0;i<=n;++i)
for(int j=0;j<=m;++j)f[i][j]=-inf;
f[0][0]=0;
for(int i=1;i<=n;++i)
{
deque<pair<ll,int> >q;
q.push_back(make_pair(f[i-1][m],m));
for(int j=m;j;--j)
{
while(!q.empty()&&q[0].second>j+s-1)q.pop_front();
while(!q.empty()&&q.back().first<=f[i-1][j-1])q.pop_back();
q.push_back(make_pair(f[i-1][j-1],j-1));
f[i][j]=q[0].first+1ll*j*a[i];
}
}
for(int i=1;i<=m;++i)ans=max(ans,f[n][i]);
cout<<ans<<endl;
return 0;
}
斜率优化DP
例题题意
将编号为 \(1\cdots n\) 的物品排成一列，每个物品长度为 \(C_i\) ，并将其装入容器中，要求每个容器中的编号连续，容器的长度为 \(i-j+\sum_{k=j}^iC_k\)
如果容器的长度为 \(x\) ，那么其花费为 \((x-L)^2\) ，\(L\) 是题目给出的常量，容器数量不限制，要求总费用最小
一句话解
先推出 \(n^2\) 的做法，然后移项后得出斜率式
用单调队列维护 \(f[j]\) 构成的凸包，上凸包还是下凸包具体题意具体分析
例题代码
deque<int>q;
ll s[maxn],f[maxn],n,L;
double slope(ll x,ll y)
{
ll Ax=f[x]+s[x]*s[x]+2*L*s[x];
ll Ay=f[y]+s[y]*s[y]+2*L*s[y];
ll Px=s[x],Py=s[y];
return (1.0*(Ax-Ay))/(1.0*(Px-Py));
}
signed main(void)
{
n=read(),L=read(),++L;
for(int i=1;i<=n;++i)s[i]=s[i-1]+read()+1;
q.push_back(0);
for(int i=1;i<=n;++i)
{
while(q.size()>1&&slope(q[0],q[1])<=2*s[i])q.pop_front();
int j=q[0];
f[i]=f[j]+s[j]*s[j]+2*L*s[j]-2*s[i]*s[j]+L*L+s[i]*s[i]-2*L*s[i];
while((j=q.size())>1&&slope(q[j-2],q[j-1])>=slope(q[j-2],i))
q.pop_back();
q.push_back(i);
}
cout<<f[n]<<endl;
return 0;
}
数据结构优化DP
例题题意
有 \(N\) 个村庄坐落在一条直线上，第 \(i(i>1)\) 个村庄距离第 \(1\) 个村庄的距离为 \(D_i\) 。需要在这些村庄中建立不超过 \(K\) 个通讯基站，在第 \(i\) 个村庄建立基站的费用为 \(C_i\)。如果在距离第 \(i\) 个村庄不超过 \(S_i\) 的范围内建立了一个通讯基站，那么就村庄被基站覆盖了。如果第 \(i\) 个村庄没有被覆盖，则需要向他们补偿，费用为 \(W_i\) 。现在的问题是，选择基站的位置，使得总费用最小。
多句话解
先得出朴素方程
一般来说朴素方程中有个别变量需要 \(O(n)\) 求解，且对于每个 \(i\) ，该变量不同
考虑用线段树维护，从 \(i-1\) 转移
线段树体现了一个区间加维护转移的作用
例题代码
int n,k,head[maxn],cnt_edge; // 前向星数组
ll c[maxn],s[maxn],w[maxn],d[maxn];// 意义与题面相同
ll f[maxn],st[maxn],ed[maxn],ans;// st,ed 记录每个节点的 L,R
struct edge// 用前向星储存每个右端点为 R 的村庄标号
{
int v,last;
}e[maxn];
struct sqtree //线段树模板
{
ll mi[maxn<<2],add[maxn<<2];
void build(int k,int l,int r)
{
add[k]=0;
if(l==r)return mi[k]=f[l],void();
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
mi[k]=min(mi[k<<1],mi[k<<1|1]);
}
void assign(int k,int val)
{
add[k]+=val;
mi[k]+=val;
}
void pushdown(int k)
{
assign(k<<1,add[k]);
assign(k<<1|1,add[k]);
add[k]=0;
}
void modify(int k,int l,int r,int x,int y,ll val)
{
if(x>y)return;
if(l>=x&&r<=y)return assign(k,val);
int mid=(l+r)>>1;
if(add[k])pushdown(k);
if(mid>=x)modify(k<<1,l,mid,x,y,val);
if(mid<y)modify(k<<1|1,mid+1,r,x,y,val);
mi[k]=min(mi[k<<1],mi[k<<1|1]);
}
ll query(int k,int l,int r,int x,int y)
{
if(x>y)return 0;
if(l>=x&&r<=y)return mi[k];
int mid=(l+r)>>1;
if(add[k])pushdown(k);
if(mid>=x&&mid>=y)return query(k<<1,l,mid,x,y);
else if(mid<y&&mid<x)return query(k<<1|1,mid+1,r,x,y);
return min(query(k<<1,l,mid,x,y),query(k<<1|1,mid+1,r,x,y));
}
}ccz;//可爱的Caicz
void addedge(int u,int v)
{
e[++cnt_edge].last=head[u];
e[cnt_edge].v=v,head[u]=cnt_edge;
}
signed main(void)
{
n=read(),k=read();
for(int i=2;i<=n;++i)d[i]=read();
for(int i=1;i<=n;++i)c[i]=read();
for(int i=1;i<=n;++i)s[i]=read();
for(int i=1;i<=n;++i)w[i]=read();
++n,++k,d[n]=inf;
k=min(k,n);
for(int i=1;i<=n;++i)// 离散化处理下标
{
st[i]=lower_bound(d+1,d+1+n,d[i]-s[i])-d;
ed[i]=lower_bound(d+1,d+1+n,d[i]+s[i])-d;
if(d[ed[i]]>d[i]+s[i])--ed[i];addedge(ed[i],i);
}
for(int g=1;g<=k;++g) // 滚动数组
if(g==1)
{
ll res=0;
for(int j=1;j<=n;++j)
{
f[j]=c[j]+res;
for(int i=head[j];i;i=e[i].last)
res+=w[e[i].v];
}
ans=f[n];
}
else
{
ccz.build(1,1,n); // 通过上一轮答案转移
for(int j=1;j<=n;++j)
{
f[j]=ccz.query(1,1,n,1,j-1)+c[j]; // 区间求 min
for(int i=head[j];i;i=e[i].last)
ccz.modify(1,1,n,1,st[e[i].v]-1,w[e[i].v]); // 区间修改
}
ans=min(ans,f[n]);// 更新答案
}
cout<<ans<<endl;
return 0;
}
数学
位运算
关于优先级
位运算的优先级低于算术运算符（除了取反），而按位与、按位或及异或低于比较运算符，所以使用时需多加注意，在必要时添加括号。
遍历某个集合的子集
// 遍历 u 的非空子集
for (int s = u; s; s = (s - 1) & u) {
// s 是 u 的一个非空子集
}
快速幂
计算 \(a^n\) 的复杂度为 \(\Theta(\log n)\) 。:
inline int fpow(int x,int y,int mod)
{
int res=1;
for(;y;x=x*x%mod,y>>=1) if(y&1) res=res*x%mod;
return res%mod;
}
矩阵快速幂
例如计算斐波拉契数列的第 \(n\) 项：
由斐波拉契数列的递推式 \(F_n=F_{n-1}+F_{n-2}\) 可以得出：
\[\begin{bmatrix}
F_n\\
F_{n-1}\\
\end{bmatrix}
=
\begin{bmatrix}
1&1\\
1&0
\end{bmatrix}
\begin{bmatrix}
F_{n-1}\\
F_{n-2}\\
\end{bmatrix}
=
\begin{bmatrix}
1&1\\
1&0
\end{bmatrix}
^n
\begin{bmatrix}
F_0\\
F_{-1}\\
\end{bmatrix}
\]
这里的 \(F_{-1}\) 是为了方便计算，可以通过递推式逆推得到 \(F_{-1}=1\) 。
代码中 \(I\) 代表单位矩阵。
struct Matrix
{
...
}I;
inline Matrix fpow(Matrix x,int y)
{
Matrix res=I;
for(;y;x=x*x,y>>=1) if(y&1) res=res*x;
return res;
}
高精度
存储
用一个数组从低位到高位存储，同时需要记录数位的长度，即最高达到哪一位。
四则运算
加法
模拟竖式加法。
void add(int a[], int b[], int c[])//a+b=c
{
clear(c);// 清空c
// 高精度实现中，一般令数组的最大长度 LEN 比可能的输入大一些
// 然后略去末尾的几次循环，这样一来可以省去不少边界情况的处理
// 因为实际输入不会超过 1000 位，故在此循环到 LEN - 1 = 1003 已经足够
for (int i = 0; i < LEN - 1; ++i)
{
// 将相应位上的数码相加
c[i] += a[i] + b[i];
if (c[i] >= 10)
{
// 进位
c[i + 1] += 1;
c[i] -= 10;
}
}
}
减法
与加法类似。
void sub(int a[], int b[], int c[])// a-b=c
{
clear(c);
for (int i = 0; i < LEN - 1; ++i)
{
// 逐位相减
c[i] += a[i] - b[i];
if (c[i] < 0)
{
// 借位
c[i + 1] -= 1;
c[i] += 10;
}
}
}
乘法
高精度乘非高精度
每一位都乘上这个数，再处理进位。
void mul_short(int a[], int b, int c[])// a*b=c
{
clear(c);
for (int i = 0; i < LEN - 1; ++i)
{
// 直接把 a 的第 i 位数码乘以乘数，加入结果
c[i] += a[i] * b;
if (c[i] >= 10)
{
// 处理进位
// c[i] / 10 即除法的商数成为进位的增量值
c[i + 1] += c[i] / 10;
// 而 c[i] % 10 即除法的余数成为在当前位留下的值
c[i] %= 10;
}
}
}
高精度乘高精度
模拟乘法乘法。
void mul(int a[], int b[], int c[])
{
clear(c);
for (int i = 0; i < LEN - 1; ++i)
{
// 这里直接计算结果中的从低到高第 i 位，且一并处理了进位
// 第 i 次循环为 c[i] 加上了所有满足 p + q = i 的 a[p] 与 b[q] 的乘积之和
// 这样做的效果和直接进行上图的运算最后求和是一样的，只是更加简短的一种实现方式
for (int j = 0; j <= i; ++j)
c[i] += a[j] * b[i - j];
if (c[i] >= 10)
{
c[i + 1] += c[i] / 10;
c[i] %= 10;
}
}
}
除法
模拟竖式除法。
参考程序实现了一个函数 greater_eq() 用于判断被除数以下标 last_dg 为最低位，是否可以再减去除数而保持非负。此后对于商的每一位，不断调用 greater_eq() ，并在成立的时候用高精度减法从余数中减去除数，也即模拟了竖式除法的过程。
// 被除数 a 以下标 last_dg 为最低位，是否可以再减去除数 b 而保持非负
// len 是除数 b 的长度，避免反复计算
inline bool greater_eq(int a[], int b[], int last_dg, int len)
{
// 有可能被除数剩余的部分比除数长，这个情况下最多多出 1 位，故如此判断即可
if (a[last_dg + len] != 0)
return true;
// 从高位到低位，逐位比较
for (int i = len - 1; i >= 0; --i)
{
if (a[last_dg + i] > b[i])
return true;
if (a[last_dg + i] < b[i])
return false;
}
// 相等的情形下也是可行的
return true;
}
void div(int a[], int b[], int c[], int d[])
{
clear(c);
clear(d);
int la, lb;
for (la = LEN - 1; la > 0; --la)
if (a[la - 1] != 0) break;
for (lb = LEN - 1; lb > 0; --lb)
if (b[lb - 1] != 0) break;
if (lb == 0)
{
puts("error");
return;
} // 除数不能为零
// c 是商
// d 是被除数的剩余部分，算法结束后自然成为余数
for (int i = 0; i < la; ++i)
d[i] = a[i];
for (int i = la - lb; i >= 0; --i)
{
// 计算商的第 i 位
while (greater_eq(d, b, i, lb))
{
// 若可以减，则减
// 这一段是一个高精度减法
for (int j = 0; j < lb; ++j)
{
d[i + j] -= b[j];
if (d[i + j] < 0)
{
d[i + j + 1] -= 1;
d[i + j] += 10;
}
}
// 使商的这一位增加 1
c[i] += 1;
// 返回循环开头，重新检查
}
}
}
素数
素数计数函数 \(\pi\)
小于等于 \(x\) 的素数个数，用 \(\pi(x)\) 表示。随着 \(x\) 的增大，有：
\[\pi(x) \approx \frac{x}{\ln x}
\]
素数判定
如果 \(x\) 是 \(a\) 的约数，那么 \(\frac{a}{x}\) 也是 \(a\) 的约数。
所以只需要判断 \(\sqrt a\) 个数是否是 \(a\) 的约数即可。
bool isPrime(int a)
{
if (a < 2) return 0;
for (int i = 2; i * i <= a; ++i)
if (a % i == 0) return 0;
return 1;
}
Miller-Rabin 素性测试
Miller-Rabin 素性测试（Miller–Rabin primality test）是进阶的素数判定方法。 对数 \(n\) 进行 \(k\) 轮测试的时间复杂度是 \(O(k\log ^3n)\) 。
Fermat 素性测试
根据费马小定理得出一种检验素数的思路：
基本思想是不断选取在 \([2,n-1]\) 中的基 \(a\) ，检验是否每次都有 \(a^{n-1}\equiv 1\pmod n\)
bool millerRabin(int n)
{
if (n < 3) return n == 2;
// test_time 为测试次数,建议设为不小于 8
// 的整数以保证正确率,但也不宜过大,否则会影响效率
for (int i = 1; i <= test_time; ++i)
{
int a = rand() % (n - 2) + 2;
if (quickPow(a, n - 1, n) != 1)
return 0;
}
return 1;
}
但是费马小定理的逆定理并不成立，换言之，满足 \(a^{n-1}\equiv 1\pmod n\) ，\(n\) 也不一定是素数。
卡迈克尔数
上面提到的一类数称作卡迈克尔数。更详细的：
对于合数 \(n\) ，如果对于所有正整数 \(a\) ， \(a\) 和 \(n\) 互素，都有同余式 \(a^{n-1} \equiv 1 \pmod n\) 成立，则合数 \(n\) 为卡迈克尔数（Carmichael Number），又称为费马伪素数。
二次探测定理
如果 \(p\) 是奇素数，则 \(x^2 \equiv 1 \pmod p\) 的解为 \(x \equiv 1\) 或者 \(x \equiv p - 1 \pmod p\) 。
证明：
\[\begin{aligned}
x^2&\equiv 1\pmod p\\
x^2-1&\equiv0\pmod p\\
(x+1)(x-1)&\equiv0\pmod p\\
x&\equiv \pm 1\pmod p
\end{aligned}
\]
实现
将费马小定理和二次探测定理结合起来使用。
将 \(n-1\) 分解成 \(2^t\times b\) ，若 \(n\) 是质数，则由费马小定理得：
\[a^{n-1}\equiv a^{2^t\times b}\equiv (a^b)^{2^t}\equiv 1\pmod n
\]
每次随机出一个数 \(a\) ，计算出 \(a^b\) ，将它自乘 \(t\) 次即可得到 \((a^b)^{2^t}\) 。
在自乘的过程中，如果自乘后的数 \(\equiv 1 \pmod n\) ，但是自乘前的数 \(\not \equiv \pm 1\pmod n\) ，那么由二次探测定理可知，\(n\) 一定不是奇素数。
bool millerRabbin(int n)
{
if (n < 3) return n == 2;
int a = n - 1, b = 0;
while (a % 2 == 0) a /= 2, ++b;
// test_time 为测试次数,建议设为不小于 8
// 的整数以保证正确率,但也不宜过大,否则会影响效率
for (int i = 1, j; i <= test_time; ++i)
{
int x = rand() % (n - 2) + 2;
int v = quickPow(x, a, n);
for (j = 0; j < b; ++j)
{
lxl nxt= 1ll * v * v % n;
if (nxt == 1 && v != 1 && v != n - 1) break;
v = nxt;
}
if (v != 1) return 0;
}
return 1;
}
最大公约数
最大公约数
辗转相除法
证明略。
int gcd(int a,int b)
{
return b ? gcd(b,a % b) : a;
}
时间复杂度 \(O(\log n)\) 。
唯一分解定理
由唯一分解定理得：
\[\begin{aligned}
a&=\prod_{i=1}^mp_i^{c_i}\\
b&=\prod_{i=1}^mp_i^{c'_i}
\end{aligned}
\]
那么由定义得：
\[\gcd(a,b)=\prod_{i=1}^mp_i^{\min(c_i,c'_i)}
\]
最小公倍数
有公式：
\[{\rm lcm}(a,b)=\frac{a\times b}{\gcd(a,b)}
\]
类似地，由唯一分解定理得：
\[{\rm lcm}(a,b)=\prod_{i=1}^mp_i^{\max(c_i,c'_i)}
\]
扩展欧几里得定理
用于求解二元一次方程 \(ax+by=\gcd(a,b)\) 的可行解。
证明
设
\[\begin{aligned}
ax_1+by_1&=\gcd(a,b)\\
bx_2+(a \ {\rm mod} \ b)y_2&=\gcd(b,a \ {\rm mod} \ b)
\end{aligned}
\]
由欧几里得定理得：
\[\begin{aligned}
\gcd(a,b)&=\gcd(b,a \ {\rm mod} \ b)\\
ax_1+by_1&=bx_2+(a \ {\rm mod} \ b)\times y_2\\
ax_1+by_1&=bx_2+(a-b\times \lfloor\frac{a}{b}\rfloor)\times y_2\\
ax_1+by_1&=ay_2+b\times (x_2-\lfloor\frac{a}{b}\rfloor \times y_2)
\end{aligned}
\]
得到：
\[\begin{aligned}
x_1&=y_2\\
y_1&=x_2-\lfloor\frac{a}{b}\rfloor \times y_2
\end{aligned}
\]
将 \(x,y\) 不断代入递归求解，直至最大公约数为 \(0\) ，返回 \(x=1,y=0\) 。
int Exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1;
y = 0;
return a;
}
int d = Exgcd(b, a % b, x, y);
int t = x;
x = y;
y = t - (a / b) * y;
return d;
}
求解线性同余方程
根据以下两个定理，我们可以求出同余方程 \(ax \equiv c \pmod b\) 的解。
定理 1 ：方程 \(ax+by=c\) 与方程 \(ax \equiv c \pmod b\) 是等价的，有整数解的充要条件为 \(\gcd(a,b) \mid c\) 。
根据定理 1，方程 \(ax+by=c\) ，我们可以先用扩展欧几里得算法求出一组 \(x_0,y_0\) ，也就是 \(ax_0+by_0=\gcd(a,b)\) ，然后两边同时除以 \(\gcd(a,b)\) ，再乘 \(c\) 。然后就得到了方程 \(a\dfrac{c}{\gcd(a,b)}x_0+b\dfrac{c}{\gcd(a,b)}y_0=c\) ，然后我们就找到了方程的一个解。
定理 2 ：若 \(\gcd(a,b)=1\) ，且 \(x_0\) 、 \(y_0\) 为方程 \(ax+by=c\) 的一组解，则该方程的任意解可表示为： \(x=x_0+bt\) ， \(y=y_0-at\) , 且对任意整数 \(t\) 都成立。
根据定理 2，可以求出方程的所有解。但在实际问题中，我们往往被要求求出一个最小整数解，也就是一个特解 \(x=(x \bmod t+t) \bmod t\) ，其中 \(t=\dfrac{b}{\gcd(a,b)}\)。
欧拉函数
定义
欧拉函数（Euler's totient function），即 \(\varphi(n)\) ，表示的是小于等于 \(n\) 和 \(n\) 互质的数的个数。
一些性质
积性函数
若 \(a \bot b\) ，有 \(\varphi(a\times b)=\varphi(a)\times \varphi(b)\) 。
\(n=\sum_{d|n}\varphi(d)\)
详见 积性函数与筛法 。
公式
设 \(n=\prod_{i=1}^mp_i^{c_i}\) ，则：
\[\varphi(n)=n\times\prod_{i=1}^m\frac{p_i-1}{p_i}
\]
证明：
-
引理：设 \(p\) 为任意质数，那么 \(\varphi(p^k)=p^{k-1}\times (p-1)\) 。
证明：显然对于从 \(1\) 到 \(p^k\) 的所有数中，除了 \(p^{k-1}\) 个 \(p\) 的倍数以外其它数都与 \(p^k\) 互素，故 \(\varphi(p^k)=p^k-p^{k-1}=p^{k-1}\times(p-1)\) ，证毕。
那么由欧拉函数的积性得：
\[\begin{aligned}
\varphi(n)&=\prod_{i=1}^m\varphi(p_i^{c_i})\\
&=\prod_{i=1}^m(p_i-1)\times p_i^{c_i-1}\\
&=\prod_{i=1}^mp_i^{c_i}\times (1-\frac{1}{p_i})\\
&=n\times \prod_{i=1}^m\frac{p_i-1}{p_i}
\end{aligned}
\]
证毕。
费马小定理
若 \(p\) 为素数， \(\gcd(a,p)=1\) ，则 \(a^{p-1}\equiv 1\pmod p\) 。
另一个形式：对于任意整数 \(a\) ，由 \(a^p\equiv a\pmod p\) 。
证明略。
欧拉定理
欧拉定理
若 \(\gcd(a, m) = 1\) ，则 \(a^{\varphi(m)} \equiv 1 \pmod{m}\) 。
证明略。
扩展欧拉定理
\[a^b\equiv
\begin{cases}
a^{b\bmod\varphi(p)},\,&\gcd(a,\,p)=1\\
a^b,&\gcd(a,\,p)\ne1,\,b<\varphi(p)\\
a^{b\bmod\varphi(p)+\varphi(p)},&\gcd(a,\,p)\ne1,\,b\ge\varphi(p)
\end{cases}
\pmod p
\]
证明略。
乘法逆元
如果一个线性同余方程 \(ax \equiv 1 \pmod b\) ，则 \(x\) 称为 \(a \bmod b\) 的逆元，记作 \(a^{-1}\) 。
求解逆元
扩展欧几里得法
求解方法与求解线性同余方程类似，详见 扩展欧几里得定理 求解线性同余方程 。
快速幂法
由费马小定理得：
\[\begin{aligned}
a^{b-1}&\equiv 1\pmod b\\
a\times a^{b-2}&\equiv 1 \pmod b\\
a^{-1}&=a^{b-2}
\end{aligned}
\]
然后就可以快速幂求了。
线性求逆元
首先有 \(1^{-1}\equiv1\pmod p\) 。
设 \(k=\lfloor\frac{p}{i}\rfloor,j=p \ {\rm mod} \ i\) ，则有 \(p=ki+j\) ，有 \(ki+j\equiv 0\pmod p\) 。
式子两边同时乘 \(i^{-1},j^{-1}\) ：
\[\begin{aligned}
kj^{-1}+i^{-1}&\equiv 0 &\pmod p\\
i^{-1}&\equiv -kj^{-1} &\pmod p\\
i^{-1}&\equiv -\lfloor\frac{p}{i}\rfloor (p \ {\rm mod} \ i)^{-1} &\pmod p
\end{aligned}
\]
inv[1] = 1;
for(int i = 2; i <= n; ++i)
inv[i] = 1ll * (p - p / i) * inv[p % i] % p;
线性求任意 n 个数的逆元
上面的方法只能求 \(1\) 到 \(n\) 的逆元，如果需要求任意给定 \(n\) 个数（ \(1 \le a_i < p\) ）的逆元，就需要下面的方法：
首先计算 \(n\) 个数的前缀积，记为 \(s_i\) ，然后使用快速幂或扩展欧几里得法计算 \(s_n\) 的逆元，记为 \(sv_n\) 。
因为 \(sv_n\) 是 \(n\) 个数的积的逆元，所以当我们把它乘上 \(a_n\) 时，就会和 \(a_n\) 的逆元抵消，于是就得到了 \(a_1\) 到 \(a_{n-1}\) 的积逆元，记为 \(sv_{n-1}\) 。
同理我们可以依次计算出所有的 \(sv_i\) ，于是 \(a_i^{-1}\) 就可以用 \(s_{i-1} \times sv_i\) 求得。
所以我们就在 \(O(n + \log p)\) 的时间内计算出了 \(n\) 个数的逆元。
s[0] = 1;
for (int i = 1; i <= n; ++i)
s[i] = s[i - 1] * a[i] % p;
sv[n] = qpow(s[n], p - 2);
for (int i = n; i >= 1; --i)
sv[i - 1] = sv[i] * a[i] % p;
for (int i = 1; i <= n; ++i)
inv[i] = sv[i] * s[i - 1] % p;
数论
中国剩余定理
中国剩余定理 (Chinese Remainder Theorem, CRT) 可求解如下形式的一元线性同余方程组（其中 \(n_1, n_2, \cdots, n_k\) 两两互质）：
\[\begin{cases}
x &\equiv a_1 \pmod {n_1} \\
x &\equiv a_2 \pmod {n_2} \\
&\vdots \\
x &\equiv a_k \pmod {n_k} \\
\end{cases}
\]
算法流程
- 计算所有模数的积 \(n\) ；
- 对于第 \(i\) 个方程：
- 计算 \(m_i=\frac{n}{n_i}\) ；
- 计算 \(m_i\) 在模 \(n_i\) 意义下的逆元 \(m_i^{-1}\) ；
- 计算 \(c_i=m_im_i^{-1}\) （ 不要对 \(n_i\) 取模 ）。
- 方程组的唯一解为： \(a=\sum_{i=1}^k a_ic_i \pmod n\) 。
证明：
对于任意一组同余方程 \(i,j\) ，其中 \(i\not=j\) 。因为 \(m_i\) 中含有 \(n_j\) ，所以有：
\[a_ic_i\equiv a_im_im_i^{-1}\equiv 0\pmod {n_j}
\]
另外有：
\[a_ic_i\equiv a_i\pmod {n_i}
\]
则对于任意同余方程 \(i\) ，有：
\[\sum_{i=1}^ka_ic_i\equiv a_i\pmod {n_i}
\]
证毕。
typedef long long lxl;
inline lxl CRT() // x = a_i (mod b_i)
{
lxl M=1,ans=0;
for(int i=1;i<=n;i++)
M*=b[i];
for(int i=1;i<=n;i++)
{
lxl tx,y,Mi=M/b[i];
exgcd(Mi,b[i],tx,y);
ans=(ans+a[i]*Mi*tx)%M;
}
return (ans+M)%M;
}
应用
某些计数问题或数论问题出于加长代码、增加难度、或者是一些其他不可告人的原因，给出的模数： 不是质数 ！
但是对其质因数分解会发现它没有平方因子，也就是该模数是由一些不重复的质数相乘得到。
那么我们可以分别对这些模数进行计算，最后用 CRT 合并答案。
扩展中国剩余定理
扩展中国剩余定理就是合并线性同余方程式，解决模数不互素的情况。
合并两个同余方程组
合并同余方程组：
\[\begin{cases}
x\equiv a_1\pmod {n_1}\\
x\equiv a_2\pmod {n_2}
\end{cases}
\implies\\
\begin{cases}
x=a_1+k_1\times n_1\\
x=a_2+k_2\times n_2
\end{cases}
\implies\\
a_1+k_1\times n_1=a_2+k_2\times n_2
\implies\\
k_1\times n_1+k_2\times n_2=a_2-a_1\\
k_1,k_2\in\Z
\]
如果方程有解，使用扩展欧几里得定理求出 \(k_1\) 的一个特解 \(k_0\) ，则 \(k_1\) 的通解为：
\[k_1=k_0+u\times \frac{n_2}{\gcd(n_1,n_2)},u\in\Z
\]
则有：
\[\begin{aligned}
x&=a_1+k_1\times n_1\\
&=a_1+(k_0+u\times \frac{n_2}{\gcd(n_1,n_2)})\times n_1\\
&=a_1+k_0\times n_1+u\times\frac{n_1\times n_2}{\gcd(n_1,n_2)}\\
&=a_1+k_0\times n_1+u\times {\rm lcm}(n_1,n_2),u\in\Z\\
x&\equiv a_1+k_0\times n_1\pmod {{\rm lcm} (n_1,n_2)}
\end{aligned}
\]
于是就把两个同余方程式合并成了一个。
合并多个同余方程组
用上面的方法两两合并就可以了。
inline lxl ExCRT()// x=a_i (mod b_i)
{
lxl ans=a[1],M=b[1];
for(int i=2;i<=n;++i)
{
lxl c=(a[i]-ans%b[i]+b[i])%b[i];
lxl b1=M,b2=b[i],x,y;
lxl d=exgcd(b1,b2,x,y);
c/=d,b2/=d;
x=quickmul(x,c,b2);
M*=b[i]/d;
ans=(ans+x*b1%M+M)%M;
}
return ans;
}
卢卡斯定理
求解方式
Lucas 定理内容如下：对于质数 \(p\) ，有
\[\binom{n}{m}\bmod p = \binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}\cdot\binom{n\bmod p}{m\bmod p}\bmod p
\]
观察上述表达式，可知 \(n\bmod p\) 和 \(m\bmod p\) 一定是小于 \(p\) 的数，可以直接求解， \(\displaystyle\binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}\) 可以继续用 Lucas 定理求解。这也就要求 \(p\) 的范围不能够太大，一般在 \(10^5\) 左右。边界条件：当 \(m=0\) 的时候，返回 \(1\) 。
时间复杂度为 \(O(f(p) + g(n)\log n)\) ，其中 \(f(n)\) 为预处理组合数的复杂度， \(g(n)\) 为单次求组合数的复杂度。
证明：
考虑 \(\displaystyle\binom{p}{n} \bmod p\) 的取值，注意到 \(\displaystyle\binom{p}{n} = \frac{p!}{n!(p-n)!}\) ，分子的质因子分解中 \(p\) 次项恰为 \(1\) ，因此只有当 \(n = 0\) 或 \(n = p\) 的时候 \(n!(p-n)!\) 的质因子分解中含有 \(p\) ，因此 \(\displaystyle\binom{p}{n} \bmod p = [n = 0 \vee n = p]\) 。进而我们可以得出
\[\begin{align}
(a+b)^p &= \sum_{n=0}^p \binom pn a^n b^{p-n}\\
&\equiv \sum_{n=0}^p [n=0\vee n=p] a^n b^{p-n}\\
&\equiv a^p + b^p \pmod p
\end{align}
\]
注意过程中没有用到费马小定理，因此这一推导不仅适用于整数，亦适用于多项式。因此我们可以考虑二项式 \(f(x)=(ax^n + bx^m)^p \bmod p\) 的结果
\[\begin{align}
(ax^n + bx^m)^p &\equiv a^p x^{pn} + b^p x^{pm} \\
&\equiv ax^{pn} + bx^{pm}\\
&\equiv f(x^p)
\end{align}
\]
考虑二项式 \((1+x)^n \bmod p\) ，那么 \(\displaystyle\binom n m\) 就是求其在 \(x^m\) 次项的取值。使用上述引理，我们可以得到
\[\begin{align}
(1+x)^n &\equiv (1+x)^{p\lfloor n/p \rfloor} (1+x)^{n\bmod p}\\
&\equiv (1+x^p)^{\lfloor n/p \rfloor} (1+x)^{n\bmod p}
\end{align}
\]
注意前者只有在 \(p\) 的倍数位置才有取值，而后者最高次项为 \(n\bmod p \le p-1\) ，因此这两部分的卷积在任何一个位置只有最多一种方式贡献取值，即在前者部分取 \(p\) 的倍数次项，后者部分取剩余项，即 \(\displaystyle\binom{n}{m}\bmod p = \binom{\left\lfloor n/p \right\rfloor}{\left\lfloor m/p\right\rfloor}\cdot\binom{n\bmod p}{m\bmod p}\bmod p\) 。
证毕。
typedef long long lxl;
lxl Lucas(lxl n, lxl m, lxl p)
{
if (m == 0) return 1;
return (C(n % p, m % p, p) * Lucas(n / p, m / p, p)) % p;
}
扩展卢卡斯定理
Lucas 定理中对于模数 \(p\) 要求必须为素数，那么对于 \(p\) 不是素数的情况，就需要用到 exLucas 定理。
设 \(ans={n\choose m} \bmod p\)。
将 \(p\) 分解质因数：
\[p=p_1^{k_1} \times p_2^{k_2} \times ... \times p_x^{k_x}
\]
则有：
\[\begin{cases}
ans \equiv c_1 \pmod {p_1^{k_1}} \\
ans \equiv c_2 \pmod {p_2^{k_2}} \\
\cdots \\
ans \equiv c_x \pmod {p_x^{k_x}}
\end{cases}
\]
其中 \(c_i={n\choose m} \bmod p_i^{k_i}\)。
也就是说，求解 \(c_i\) 后，再用CRT合并同余方程组即可求出 \(ans\)。
如何求解 \(c_i\) ：
\[c_i=\frac{n!}{m!(n-m)!} \ {\rm {mod}} \ p_i^{k_i}
\]
注意到 \(m!,(n-m)!\) 与 \(p_i^{k_i}\) 不一定互素，不能直接求解逆元。
考虑将 \(n!,m!,(n-m)!\) 中 \(p_i\) 因子除去，使其与 \(p_i^{k_i}\) 互素：
\[\frac{\frac{n!}{p_i^x}}{\frac{m!}{p_i^y} \ \frac{(n-m)!}{p_i^z}} \times p_i^{x-y-z} \ {\rm {mod}} \ p_i^{k_i}
\]
其中 \(x,y,z\) 分别为 \(n!,m!,(n-m)!\) 中 \(p_i\) 因子的个数。
此时即可用逆元求解。
如何求解 \(\frac{n!}{p_i^x}\) 。
对 \(n!\) 进行变形：
\[\begin{aligned}
n!&=1 \times 2 \times 3 \times ... \times n\\
&=(p_i \times 2p_i \times ...)\prod_{i=1,i \not \equiv 0 \ {\rm {mod}} \ p_i} ^{n} i\\
&=p_i^{\lfloor \frac {n}{p_i} \rfloor} \times {\lfloor \frac {n}{p_i} \rfloor}! \times \prod_{i=1,i \not \equiv 0 \ {\rm {mod}} \ p_i} ^{n} i
\end{aligned}
\]
可以发现其中 \(\prod_{i=1,i \not \equiv 0 \ {\rm {mod}} \ p_i} ^{n} i\) 是有循环节的，可以暴力求，例如：
\[\begin{aligned}
22! &\equiv (1⋅2⋅4⋅5⋅7⋅8)\times (10⋅11⋅13⋅14⋅16⋅17)\times\\
&(19⋅20⋅22)\times (3⋅6⋅9⋅12⋅15⋅18⋅21)\pmod {3^2}\\
&\equiv(1\cdot 2\cdot 4\cdot 5\cdot 7\cdot 8)^2\times (19\cdot 20\cdot 22)\times 3^7\times\\
&(1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7)\pmod {3^2}\\
&\equiv 3^7\times 7!\times (1\cdot 2\cdot 4\cdot 5\cdot 7\cdot 8)^2\times (19\cdot 20\cdot 22)\pmod{3^2}\\
\end{aligned}
\]
所以：
\[=p_i^{\lfloor \frac {n}{p_i} \rfloor} \times {\lfloor \frac {n}{p_i} \rfloor}! \times (\prod_{i=1,i \not \equiv 0 \ {\rm {mod}} \ p_i} ^{p_i^{k_i}} i)^{\lfloor \frac {n}{p_i^{p_k}} \rfloor} \times \prod_{i=p_i^{k_i} \times \lfloor \frac {n}{p_i^{k_i}} \rfloor,i \not \equiv 0 \ {\rm {mod}} \ p_i} ^{n} i
\]
发现其中 \({\lfloor \frac {n}{p_i} \rfloor}!\) 和 \(n!\) 的求解方法是一样的，递归求解即可。
inline lxl mul(lxl n,lxl pi,lxl pk)
{
if(!n) return 1;
lxl ans=1;
if(n/pk)
{
for(lxl i=1;i<=pk;i++)
if(i%pi) ans=ans*i%pk;
ans=quickpow(ans,n/pk,pk);
}
for(lxl i=2;i<=n%pk;i++)
if(i%pi) ans=ans*i%pk;
return ans*mul(n/pi,pi,pk)%pk;
}
inline lxl C(lxl n,lxl m,lxl p,lxl pi,lxl pk)
{
if(n<m) return 0;
lxl a=mul(n,pi,pk),b=mul(m,pi,pk),c=mul(n-m,pi,pk),k=0,ans;
for(lxl i=n;i;i/=pi) k+=i/pi;
for(lxl i=m;i;i/=pi) k-=i/pi;
for(lxl i=n-m;i;i/=pi) k-=i/pi;
ans=a*inv(b,pk)%pk*inv(c,pk)%pk*quickpow(pi,k,pk)%pk;
ans=ans*(p/pk)%p*inv(p/pk,pk)%p;
return ans;
}
inline lxl exLucas(lxl n,lxl m,lxl p)
{
lxl ans=0,x=p,t=sqrt(p);
for(lxl i=2;i<=t;i++)
if(x%i==0)
{
lxl pk=1;
while(x%i==0) x/=i,pk=pk*i%p;
ans=(ans+C(n,m,p,i,pk))%p;
}
if(x>1) ans=(ans+C(n,m,p,x,x))%p;
return ans;
}
积性函数与筛法
定义
若函数 \(f(n)\) 满足 \(f(1)=1\) 且 \(\forall x,y \in {\Bbb{N}}_{+},{\rm{gcd}}(x,y)=1\) 都有 \(f(xy)=f(x)f(y)\) ，则 \(f\) 为积性函数。
若函数 \(f(n)\) 满足 \(f(1)=1\) 且 \(\forall x,y \in {\Bbb{N}}_{+}\) 都有 \(f(xy)=f(x)f(y)\) ，则 \(f\) 为完全积性函数。
性质
比较重要的有：若 \(f,g\) 为积性函数，则满足
\[h(n)=\sum_{d|n}f(d)g(\frac{n}{d})
\]
的函数 \(h\) 也为积性函数。
函数 \(h\) 称作 \(f,g\) 的Dirichlet卷积，记作 \(f*g\) 。
例子
单位函数
\[\epsilon(n)=[n=1]
\]
有：
\[\epsilon=\mu*{\rm{I}} \iff \epsilon(n)=\sum_{d|n}\mu(d)
\]
这个式子尤其常用。
任何函数卷 \(\epsilon\) 都为其本身。
恒等函数
\[{\rm{id}}_k(n)=n^k
\]
一般用 \({\rm{id}}\) 表示 \({\rm{id}}_1\) 。
常数函数
\[{\rm{I}}(n)=1
\]
在杜教筛中有用到。
除数函数
\[\sigma_k(n)=\sum_{d|n}d^k
\]
一般 \(\sigma_0\) 记作 \({\rm{d}}\) ，\(\sigma_1\) 记作 \(\sigma\) 。
对于 \(\sigma\) ，有：
\[\sigma={\rm{id}}*{\rm{I}} \iff \sigma(n)=\sum_{d|n}d
\]
线性筛 \({\rm{d}}\)
设 \(n=\prod_{i=1}^mp_i^{c_i}\) ，则根据乘法原理有：
\[{\rm{d}}(n)=\prod_{i=1}^m(c_i+1)
\]
- 对于质数 \(p\) ，有 \({\rm{d}}(p)=2\) 。
- 对于 \(a,b\) 满足 \(a\bot b\) ，有 \({\rm{d}}(ab)={\rm{d}}(a){\rm{d}}(b)\) 。
- 对于质数 \(p\) 与合数 \(a\) 满足 \(p|a\) ，设 \(c\) 为 \(p\) 在 \(pa\) 中的次数，有 \({\rm{d}}(pa)={\rm{d}}(a)\frac{c+1}{c}\) 。
于是就可以线性筛了：
\(num_i\) 记录 \(i\) 的最小质因子的次数。
inline void sieve()
{
d[1]=1;
for(int i=2;i<=N;++i)
{
if(!flag[i]) prime[++cnt]=i,d[i]=2,num[i]=1;
for(int j=1;j<=cnt&&i*prime[j]<=N;++j)
{
flag[i*prime[j]]=true;
if(i%prime[j])
{
num[i*prime[j]]=1;
d[i*prime[j]]=d[i]*2;
}
else
{
num[i*prime[j]]=num[i]+1;
d[i*prime[j]]=d[i]/num[i*prime[j]]*(num[i*prime[j]]+1);
break;
}
}
}
}
线性筛 \(\sigma\)
由乘法原理得：
\[\sigma(n)=\prod_{i=1}^m\sum_{j=0}^{c_i}p_i^j
\]
令 \(f\) 记录约数和，\(g\) 记录最小质因子 \(p\) 的 \(\sum_{i=0}^{c}p^i\) 。则有：
- 对于质数 \(p\) ，有 \(f(p)=1+p,g(n)=1+p\) 。
- 对于 \(a,b\) 满足 \(a \bot b\) ，且 \(ab\) 的最小质因子为 \(p\) ，有 \(f(ab)=f(a)f(b),g(ab)=\sum_{i=0}^{c}p^i\) 。
- 对于质数 \(p\) 和合数 \(a\) 且 \(p\) 是 \(a\) 的最小质因子，有 \(g(pa)=g(a)\times p+1,f(pa)=f(a)\frac{g(pa)}{g(a)}\)
inline void sieve()
{
f[1]=g[1]=1;
for(int i=2;i<=N;++i)
{
if(!flag[i]) prime[++cnt]=i,f[i]=g[i]=1+i;
for(int j=1;j<=cnt&&i*prime[j]<=N;++j)
{
flag[i*prime[j]]=true;
if(i%prime[j])
{
f[i*prime[j]]=f[i]*f[prime[j]];
g[i*prime[j]]=1+prime[j];
}
else
{
g[i*prime[j]]=g[i]*prime[j]+1;
f[i*prime[j]]=f[i]/g[i]*g[i*prime[j]];
break;
}
}
}
}
欧拉函数
\[\varphi(n)=\sum_{i=1}^n[i\bot n]
\]
设 \(n=\prod_{i=1}^mp_i^{c_i}\) ，则有通式：
\[\varphi(n)=n\times \prod_{i=1}^m\frac{p_i-1}{p_i}
\]
有：
\[\varphi * {\rm{I}}={\rm{id}}
\]
证明：
因为 \(\varphi\) 是积性函数，所以只需要证明 \(n=p^c\) 的情况，即证明：
\[(\varphi*{\rm{I}})(n)=\sum_{d|n}\varphi(d)={\rm{id}}(n)
\]
因为 \(n=p^c\) 所以 \(d=1,p,p^2,p^3 \cdots,p^c\) ，将上式改为枚举 \(p\) 的次数：
\[\begin{align}
\sum_{d|n}\varphi(d)&=\sum_{i=0}^c\varphi(p^i)\\
&=1+p^0(p-1)+p^1(p-1)+\cdots+p^{c-1}(p-1)\\
&=p^c\\
&={\rm{id}}(n)
\end{align}
\]
上面用到了欧拉函数的性质： \(\varphi(p^c)=p^{c-1}(p-1)\) 。
\(\varphi*{\rm{I}}={\rm{id}}\) 得证。
线性筛 \(\varphi\)
- 对于质数 \(p\) ，有 \(\varphi(p)=p-1\) 。
- 对于 \(a,b\) 满足 \(a\bot b\) ，有 \(\varphi(ab)=\varphi(a)\varphi(b)\) 。
- 对于质数 \(p\) 和数 \(a\) 满足 \(p|a\) ，有 \(\varphi(pa)=\varphi(a)\times p\) 。
对于第三种情况，证明如下：
因为 \(p|a\) ，所以 \(a\) 包含了所有 \(pa\) 的质因子，则有：
\[\begin{align}
\varphi(pa)&=p\times a\prod_{i=1}^m\frac{p_i-1}{p_i}\\
&=p\times\varphi(a)
\end{align}
\]
证毕。
inline void sieve()
{
phi[1]=1;
for(int i=2;i<=N;i++)
{
if(!flag[i]) prime[++cnt]=i,phi[i]=i-1;
for(int j=1;j<=cnt&&prime[j]*i<=N;j++)
{
flag[prime[j]*i]=true;
if(i%prime[j]==0)
{
phi[prime[j]*i]=phi[i]*prime[j];
break;
}
else phi[prime[j]*i]=phi[i]*(prime[j]-1);
}
}
}
莫比乌斯函数
\[\mu(n)=\begin{cases}1 & n=1\\ 0 & \exists d>1:d^2|n \\ (-1)^{\omega(n)} & \text{otherwise}\end{cases}
\]
其中 \(\omega(n)\) 表示 \(n\) 不同质因子个数。
有：
\[\sum_{d|n}\mu(d)=\epsilon(n) \iff \epsilon=\mu*{\rm{I}}
\]
证明：
令 \(n=\prod_{i=1}^mp_i^{c_i},n'=\prod_{i=1}^mp_i\) ，则：
\[\begin{align}
\sum_{d|n}\mu(d)&=\sum_{d|n'}\mu(d)\\
&=\sum_{i=0}^m{m \choose i}\times 1\times (-1)^i\\
&=(1+(-1))^k\\
&=\begin{cases}1 & k=0 \\ 0 & k \not =0\end{cases}\\
&=\begin{cases}1 & n=1 \\ 0 & n \not =1\end{cases}\\
&=\epsilon(n)
\end{align}
\]
这同时也证明了 \(\epsilon=\mu*{\rm{I}}\) 。
证毕。
与欧拉函数结合，有：
\[\varphi=\mu*{\rm{id}} \iff \varphi(n)=\sum_{d|n}d\cdot\mu(\frac{n}{d})
\]
证明：
\[\varphi*{\rm{I}}={\rm{id}} \iff \varphi*{\rm{I}}*\mu={\rm{id}}*\mu \iff \varphi=\mu*{\rm{id}}
\]
上面用到了 \(\mu*{\rm{I}}=\epsilon\) 的结论。
证毕。
反演结论
\[[{\rm{gcd}}(i,j)=1] \iff \sum_{d|i,d|j}\mu(d)
\]
线性筛 \(\mu\)
- 对于质数 \(p\) ，有 \(\mu(p)=-1\) 。
- 对于 \(a,b\) 满足 \(a\bot b\) ，有 \(\mu(ab)=\mu(a)\mu(b)\) 。
- 对于质数 \(p\) 和整数 \(a\) 满足 \(p|a\) ，有 \(\mu(pa)=0\) 。
inline void sieve()
{
mu[1]=1;
for(int i=2;i<=N;++i)
{
if(!flag[i]) prime[++cnt]=i,mu[i]=-1;
for(int j=1;j<=cnt&&i*prime[j]<=N;++j)
{
flag[i*prime[j]]=true;
if(!(i%prime[j])) break;
mu[i*prime[j]]=-mu[i];
}
}
}
排列组合
排列数
从 \(n\) 个不同元素中，任取 \(m\) （ \(m\leq n\) ， \(m\) 与 \(n\) 均为自然数，下同）个元素按照一定的顺序排成一列，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个排列；从 \(n\) 个不同元素中取出 \(m\) ( \(m\leq n\) ) 个元素的所有排列的个数，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的排列数，用符号 \(\mathrm A_n^m\) （或者是 \(\mathrm P_n^m\) ）表示。
排列的计算公式如下：
\[\mathrm A_n^m = n(n-1)(n-2) \cdots (n-m+1) = \frac{n!}{(n - m)!}
\]
组合数
从 \(n\) 个不同元素中，任取 \(m\) ( \(m\leq n\) ) 个元素组成一个集合，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个组合；从 \(n\) 个不同元素中取出 \(m\) ( \(m\leq n\) ) 个元素的所有组合的个数，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的组合数。用符号 \(\mathrm C_n^m\) 来表示，更常用的符号是 \({n\choose m}\) 。
组合数计算公式
\[\mathrm C_n^m = \frac{\mathrm A_n^m}{m!} = \frac{n!}{m!(n - m)!}
\]
二项式定理
二项式定理阐明了一个展开式的系数：
\[(a+b)^n=\sum_{i=0}^n\binom{n}{i}a^{n-i}b^i
\]
错位排列
若一个排列使得所有的元素不在原来的位置上，则称这个排列为错排。
错位排列的递推式为 \(f(n)=(n-1)(f(n-1)+f(n-2))\) 。
圆排列
\(n\) 个人全部来围成一圈，所有的排列数记为 \(\mathrm Q_n^n\) 。考虑其中已经排好的一圈，从不同位置断开，又变成不同的队列。
所以有
\[\mathrm Q_n^n \times n = \mathrm A_n^n \Longrightarrow \mathrm Q_n = \frac{\mathrm A_n^n}{n} = (n-1)!
\]
由此可知部分圆排列的公式：
\[\mathrm Q_n^r = \frac{\mathrm A_n^r}{r} = \frac{n!}{r \times (n-r)!}
\]
组合数性质 | 二项式推论
由于组合数在 OI 中十分重要，因此在此介绍一些组合数的性质。
\[\binom{n}{m}=\binom{n}{n-m}\tag{1}
\]
相当于将选出的集合对全集取补集，故数值不变。（对称性）
\[\binom{n}{k} = \frac{n}{k} \binom{n-1}{k-1}\tag{2}
\]
由定义导出的递推式。
\[\binom{n}{m}=\binom{n-1}{m}+\binom{n-1}{m-1}\tag{3}
\]
组合数的递推式（杨辉三角的公式表达）。我们可以利用这个式子，在 \(O(n^2)\) 的复杂度下推导组合数。
\[\binom{n}{0}+\binom{n}{1}+\cdots+\binom{n}{n}=\sum_{i=0}^n\binom{n}{i}=2^n\tag{4}
\]
这是二项式定理的特殊情况。取 \(a=b=1\) 就得到上式。
\[\sum_{i=0}^n(-1)^i\binom{n}{i}=0\tag{5}
\]
二项式定理的另一种特殊情况，可取 \(a=1, b=-1\) 。
\[\sum_{i=0}^m \binom{n}{i}\binom{m}{m-i} = \binom{m+n}{m}\ \ \ (n \geq m)\tag{6}
\]
拆组合数的式子，在处理某些数据结构题时会用到。
\[\sum_{i=0}^n\binom{n}{i}^2=\binom{2n}{n}\tag{7}
\]
这是 \((6)\) 的特殊情况，取 \(n=m\) 即可。
\[\sum_{i=0}^ni\binom{n}{i}=n2^{n-1}\tag{8}
\]
带权和的一个式子，通过对 \((3)\) 对应的多项式函数求导可以得证。
\[\sum_{i=0}^ni^2\binom{n}{i}=n(n+1)2^{n-2}\tag{9}
\]
与上式类似，可以通过对多项式函数求导证明。
\[\sum_{l=0}^n\binom{l}{k} = \binom{n+1}{k+1}\tag{10}
\]
可以通过组合意义证明，在恒等式证明中较常用。
\[\binom{n}{r}\binom{r}{k} = \binom{n}{k}\binom{n-k}{r-k}\tag{11}
\]
通过定义可以证明。
\[\sum_{i=0}^n\binom{n-i}{i}=F_{n+1}\tag{12}
\]
其中 \(F\) 是斐波那契数列。
\[\sum_{l=0}^n \binom{l}{k} = \binom{n+1}{k+1}\tag{13}
\]
通过组合分析——考虑 \(S={a_1, a_2, \cdots, a_{n+1}}\) 的 \(k+1\) 子集数可以得证。
卡特兰数
递推式
该递推关系的解为：
\[H_n = \frac{\binom{2n}{n}}{n+1}(n \geq 2, n \in \mathbf{N_{+}})
\]
关于 Catalan 数的常见公式：
\[H_n = \begin{cases}
\sum_{i=1}^{n} H_{i-1} H_{n-i} & n \geq 2, n \in \mathbf{N_{+}}\\
1 & n = 0, 1
\end{cases}
\]
\[H_n = \frac{H_{n-1} (4n-2)}{n+1}
\]
\[H_n = \binom{2n}{n} - \binom{2n}{n-1}
\]
路径计数问题
非降路径是指只能向上或向右走的路径。
-
从 \((0,0)\) 到 \((m,n)\) 的非降路径数等于 \(m\) 个 \(x\) 和 \(n\) 个 \(y\) 的排列数，即 \(\dbinom{n + m}{m}\) 。
-
从 \((0,0)\) 到 \((n,n)\) 的除端点外不接触直线 \(y=x\) 的非降路径数：
先考虑 \(y=x\) 下方的路径，都是从 \((0, 0)\) 出发，经过 \((1, 0)\) 及 \((n, n-1)\) 到 \((n,n)\) ，可以看做是 \((1,0)\) 到 \((n,n-1)\) 不接触 \(y=x\) 的非降路径数。
所有的的非降路径有 \(\dbinom{2n-2}{n-1}\) 条。对于这里面任意一条接触了 \(y=x\) 的路径，可以把它最后离开这条线的点到 \((1,0)\) 之间的部分关于 \(y=x\) 对称变换，就得到从 \((0,1)\) 到 \((n,n-1)\) 的一条非降路径。反之也成立。从而 \(y=x\) 下方的非降路径数是 \(\dbinom{2n-2}{n-1} - \dbinom{2n-2}{n}\) 。根据对称性可知所求答案为 \(2\dbinom{2n-2}{n-1} - 2\dbinom{2n-2}{n}\) 。
-
从 \((0,0)\) 到 \((n,n)\) 的除端点外不穿过直线 \(y=x\) 的非降路径数：
用类似的方法可以得到： \(\dfrac{2}{n+1}\dbinom{2n}{n}\) 。
概率与期望
事件
单位事件、事件空间、随机事件
在一次随机试验中可能发生的不能再细分的结果被称为单位事件，用 \(E\) 表示。在随机试验中可能发生的所有单位事件的集合称为事件空间，用 \(S\) 来表示。例如在一次掷骰子的随机试验中，如果用获得的点数来表示单位事件，那么一共可能出现 \(6\) 个单位事件，则事件空间可以表示为 \(S=\{1,2,3,4,5,6\}\) 。
随机事件是事件空间 \(S\) 的子集，它由事件空间 \(S\) 中的单位元素构成，用大写字母 \(A, B, C,\ldots\) 表示。例如在掷两个骰子的随机试验中，设随机事件 \(A\) 为“获得的点数和大于 \(10\) ”，则 \(A\) 可以由下面 \(3\) 个单位事件组成： \(A = \{ (5,6),(6,5),(6,6)\}\) 。
事件的计算
因为事件在一定程度上是以集合的含义定义的，因此可以把集合计算方法直接应用于事件的计算，也就是说，在计算过程中，可以把事件当作集合来对待。
和事件 ：相当于 并集 。只需其中之一发生，就发生了。
积事件 ：相当于 交集 。必须要全都发生，才计算概率。
概率
定义
古典定义
如果一个试验满足两条：
- 试验只有有限个基本结果；
- 试验的每个基本结果出现的可能性是一样的；
这样的试验便是古典试验。
对于古典试验中的事件 \(A\) ，它的概率定义为 \(P(A)=\frac{m}{n}\) ，其中 \(n\) 表示该试验中所有可能出现的基本结果的总数目， \(m\) 表示事件 \(A\) 包含的试验基本结果数。
统计定义
如果在一定条件下，进行了 \(n\) 次试验，事件 \(A\) 发生了 \(N_A\) 次，如果随着 \(n\) 逐渐增大，频率 \(\frac{N_A}{n}\) 逐渐稳定在某一数值 \(p\) 附近，那么数值 \(p\) 称为事件 \(A\) 在该条件下发生的概率，记做 \(P(A)=p\) 。
公理化定义
设 \(E\) 是随机试验， \(S\) 是它的样本空间。对 \(E\) 的每一个事件 \(A\) 赋予一个实数，记为 \(P(A)\) ，称为事件 \(A\) 的概率，这里 \(P(A)\) 是一个集合函数， \(P(A)\) 满足下列条件：
-
非负性 ：对于一个事件 \(A\) ，有概率 \(P(A)\in [0,1]\) 。
-
规范性 ：事件空间的概率值为 \(1\) ， \(P(S)=1\) .
-
容斥性 ：若 \(P(A+B) = P(A)+P(B)\) ，则 \(A\) 和 \(B\) 互为独立事件。
计算
- 广义加法公式 : 对任意两个事件 \(A,B\) ， \(P(A \cup B)=P(A)+P(B)-P(A\cap B)\)
- 条件概率 : 记 \(P(B|A)\) 表示在 \(A\) 事件发生的前提下， \(B\) 事件发生的概率，则 \(P(B|A)=\dfrac{P(AB)}{P(A)}\) （其中 \(P(AB)\) 为事件 \(A\) 和事件 \(B\) 同时发生的概率）。
- 乘法公式 : \(P(AB)=P(A)\cdot P(B|A)=P(B)\cdot P(A|B)\)
- 全概率公式 ：若事件 \(A_1,A_2,\ldots,A_n\) 构成一个完备的事件且都有正概率，即 \(\forall i,j, A_i\cap A_j=\varnothing\) 且 \(\displaystyle \sum_{i=1}^n A_i=1\) ，有 \(\displaystyle P(B)=\sum_{i=1}^n P(A_i)P(B|A_i)\) 。
- 贝叶斯定理 ： \(\displaystyle P(B_i|A)=\frac{P(B_i)P(A|B_i)}{\displaystyle \sum_{j=1}^n P(B_j)P(A|B_j)}\)
期望
定义
在一定区间内变量取值为有限个，或数值可以一一列举出来的变量称为离散型随机变量。一个离散性随机变量的数学期望是试验中每次可能的结果乘以其结果概率的总和。
\[E(x)=\sum\limits_{\omega\in\Omega}X(\omega)Pr(\omega)
\]
性质
- 全期望公式 ： \(E(Y)=E[E(Y|X)]\) 。可由全概率公式证明。
- 线性性质 1 : 对于任意两个随机变量 \(X,Y\) （ 不要求相互独立 ），有 \(E(X+Y)=E(X)+E(Y)\) 。利用这个性质，可以将一个变量拆分成若干个互相独立的变量，分别求这些变量的期望值，最后相加得到所求变量的值。
- 线性性质 2 : 当两个随机变量 \(X,Y\) 相互独立时，有 \(E(XY)=E(X)E(Y)\) 。
例题
试卷上共有 \(n\) 道单选题，第 \(i\) 道单选题有 \(a_i\) 个选项，每个选项成为正确答案的概率都是相等的。你做对了所有题，但是你填答题卡的时候不小心把第 \(i\) 道题的答案填到第 \(i+1\) 道题上了，特殊的，第 \(n\) 道题的答案填到了第 \(i\) 道题上。求最后你期望做对多少道题。
题解
做对后一题的概率是古典概率，其两个要素是
- 所有可能的结果：两道题可能选项的所有组合，共 \(a_{i-1}\times a_i\) 种；
- 需要计算的结果：两道题的答案一样，共 \(\min\{a_{i-1},a_i\}\) 种。
那么第 \(i\) 道题对答案贡献的期望是 \(1\times \frac{\min\{a_{i-1},a_i\}}{a_{i-1}\times a_i}\) ，由期望的线性性得答案为：
\[\sum_{i=1}^n\frac{\min\{a_{i-1},a_i\}}{a_{i-1}\times a_i}
\]
图论
第一节 最短路
\(Floyd\)
- \(O(n^3)\)
- 模板题（弱化版）\(40\) 分拿全 \(16ms\)
- 可判负环
#include<cstdio>
#include<iostream>
using namespace std;
int n,m,s;
int dis[110][110];
int main(){
for(int i=1;i<=100;i=-~i)for(int j=i+1;j<=100;j=-~j)dis[i][j]=dis[j][i]=114141919;
scanf("%d%d%d",&n,&m,&s);
for(int i=1,u,v,wt;i<=m;i=-~i)
scanf("%d%d%d",&u,&v,&wt),dis[u][v]=min(dis[u][v],wt);
for(int k=1;k<=n;k=-~k)
for(int i=1;i<=n;i=-~i)
for(int j=1;j<=n;j=-~j)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
for(int i=1;i<=n;i=-~i)
if(dis[s][i]!=114141919)printf("%d ",dis[s][i]);else printf("2147483647 ");
return 0;
}
\(SPFA\)
\(O(kn)\)
- 模板题（弱化版） \(388ms\)
- +\(SLF\) \(361ms\)
- +\(LLL\) \(394ms\)
- +\(SLF\)+\(LLL\) \(367ms\)
- 可判负环
#include<deque>
#include<queue>
#include<cstdio>
#include<cstring>
using namespace std;
const int inf=0x3f3f3f3f;
struct Edge{
int v,w,nxt;
}e[500011];
int n,m,s;
int dis[10011];
int head[10011],cnt;
bool inq[10011];
void add_Edge(int u,int v,int w){e[++cnt]=(Edge){v,w,head[u]};head[u]=cnt;}
void SPFA()
{
for(int i=1;i<=n;++i)dis[i]=inf;
dis[s]=0;inq[s]=1;
queue<int>q;
q.push(s);
while(!q.empty())
{
int u=q.front();inq[u]=0;q.pop();
for(int i=head[u];i;i=e[i].nxt)
if(dis[e[i].v]>dis[u]+e[i].w)
{
dis[e[i].v]=dis[u]+e[i].w;
if(!inq[e[i].v])q.push(e[i].v),inq[e[i].v]=1;
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&s);
for(int i=1,u,v,w;i<=m;++i)
scanf("%d%d%d",&u,&v,&w),add_Edge(u,v,w);
SPFA();
for(int i=1;i<=n;++i)
if(dis[i]!=inf)printf("%d ",dis[i]);else printf("2147483647 ");
return 0;
}
\(dijkstra\)
-
朴素 \(O(n^2)\)
-
使用堆优化 \(O(nlogn)\)
- 朴素 模板 \(TLE\) 完
- 堆优化 模板 \(729ms\)
- 不能有负边权
struct node{
int dis,pos;
bool friend operator < (node a,node b){
return a.dis>b.dis;
}
};
void add_Edge(int u,int v,int w){e[++cnt]=(Edge){v,w,head[u]};head[u]=cnt;}
void dijkstra(){
memset(dis,63,sizeof(dis));dis[s]=0;
for(int i=1;i<=n;++i){
int minn=inf,min_point=0;
for(int j=1;j<=n;++j)
if(dis[j]<minn&&!vis[j])minn=dis[j],min_point=j;
if(!min_point)break;
vis[min_point]=1;
for(int j=head[min_point];j;j=e[j].nxt)
dis[e[j].v]=min(dis[e[j].v],dis[min_point]+e[j].w);
}
}//没优化版
void dijkstra(){
priority_queue<node>pq;
memset(dis,63,sizeof(dis));dis[s]=0;
pq.push((node){0,s});
while(!pq.empty()){
int u=pq.top().pos,d=pq.top().dis;
pq.pop();
if(vis[u])continue;
vis[u]=1;
for(int i=head[u];i;i=e[i].nxt)
if(dis[e[i].v]>d+e[i].w){
dis[e[i].v]=d+e[i].w;
if(!vis[e[i].v])pq.push((node){dis[e[i].v],e[i].v});
}
}
}
第二节 最近公共祖先\(lca\)
倍增
-
时间:\(O(\log n)\)
-
空间:\(O(n\log n)\)
-
预处理:\(O(n\log n)\)
-
\(online\)
namespace DoubleStepLca{
int f[MAXN][MAXL],dep[MAXN],lg[MAXN];
#define v e[i].to
void dfs(int u,int fa){
f[u][0]=fa;dep[u]=dep[fa]+1;
for(register int i=1;i<=lg[dep[u]];++i) f[u][i]=f[f[u][i-1]][i-1];
edge(u) (v!=fa)&&(dfs(v,u),1);
}
#undef v
inline int lca(int u,int v){
if(dep[u]<dep[v]) swap(u,v);
for(register int i=lg[dep[u]-dep[v]+1];~i;--i)
(dep[f[u][i]]>=dep[v])&&(u=f[u][i]);//这里优化了一下
if(u==v) return u;
for(register int i=lg[dep[u]];~i;--i)
(f[u][i]!=f[v][i])&&(u=f[u][i],v=f[v][i]);
return f[u][0];
}
int main(){
register int i;
n=read(),m=read();root=read();
BuildGraph(n-1);lg[0]=-1;
for(i=1;i<=n;++i) lg[i]=lg[i>>1]+1;
dfs(root,0);
for(i=1;i<=m;++i) printf("%d\n",lca(read(),read()));
return 0;
}
}
树剖
- 时间：\(O(\log n)\)
- 空间：\(O(n)\)
- 预处理：\(O(n)\)
- \(online\)
代码简洁
namespace LinkDivideLca{
int dep[MAXN],father[MAXN],size[MAXN],son[MAXN],top[MAXN];
#define v e[i].to
void dfs(int u,int fa){
dep[u]=dep[fa]+1;father[u]=fa;size[u]=1;
edge(u){
if(v==fa) continue;dfs(v,u);
size[u]+=size[v];if(size[son[u]]<size[v]) son[u]=v;
}
}
void df5(int u,int link){
top[u]=link;if(son[u]) df5(son[u],link);
edge(u) (!top[v])&&(df5(v,v),1);
}
#undef v
inline int lca(int u,int v){
for(;top[u]^top[v];dep[top[u]]>dep[top[v]]?u=father[top[u]]:v=father[top[v]]);
return dep[u]<dep[v]?u:v;
}
int main(){
register int i;
n=read(),m=read();root=read();
BuildGraph(n-1);
dfs(root,0);df5(root,root);
for(i=1;i<=m;++i) printf("%d\n",lca(read(),read()));
return 0;
}
}
\(RMQ\)
- 时间：\(O(1)\)
- 空间：\(O(2n\log n)\)
- 预处理：\(O(2n\log n)\)
- \(online\)
- 常数大！
namespace RMQLca{
int dfn[MAXN<<1],dep[MAXN<<1],first[MAXN],lg[MAXN<<1];
int table[MAXN<<1][MAXL+1],pos[MAXN<<1][MAXL+1];
#define v e[i].to
#define cnt dfn[0]
void dfs(int u,int fa,int depth){
dfn[first[u]=++cnt]=u;dep[cnt]=depth;
edge(u){
if(v==fa) continue;dfs(v,u,depth+1);
dfn[++cnt]=u;dep[cnt]=depth;
}
}
#undef v
inline void maketable(){
register int i,j;lg[0]=-1;
for(i=1;i<=cnt;++i) table[i][0]=dep[i],pos[i][0]=dfn[i],lg[i]=lg[i>>1]+1;
for(j=1;j<=lg[cnt];++j)
for(i=1;i+(1<<j)-1<=cnt;++i)
if(table[i][j-1]<table[i+(1<<j-1)][j-1]) table[i][j]=table[i][j-1],pos[i][j]=pos[i][j-1];
else table[i][j]=table[i+(1<<j-1)][j-1],pos[i][j]=pos[i+(1<<j-1)][j-1];
}
#undef cnt
inline int lca(int u,int v){
u=first[u],v=first[v];
if(u>v) swap(u,v);
int x=lg[v-u+1];
if(table[u][x]<table[v-(1<<x)+1][x]) return pos[u][x];
else return pos[v-(1<<x)+1][x];
}
int main(){
register int i;
n=read(),m=read();root=read();
BuildGraph(n-1);dfs(root,0,1);maketable();
for(i=1;i<=m;++i) printf("%d\n",lca(read(),read()));
return 0;
}
}
也可以自定义结构体重载运算符，
struct Node {
int i,depth;
bool operator < (Node q)const{
return depth<q.depth;
}
}st[N<<1][20];
void dfs(int u,int fa,int depth) {
dfn[u]=++lead;
st[lead][0].i=u;
st[lead][0].depth=depth;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v==fa)continue;
dfs(v,u,depth+1);
++lead;
st[lead][0].i=u;
st[lead][0].depth=depth;
}
}
void prepare() {
dfs(S,0,0);
for(int k=1;k<=19;++k)
for(int i=1;(i+(1<<k)-1)<=lead;++i)
st[i][k]=min(st[i][k-1],st[i+(1<<(k-1))][k-1]);
}
int _lca(int x,int y) {
int l=dfn[x],r=dfn[y];
if(l>r)swap(l,r);
int k=lg[r-l+1];
return min(st[l][k],st[r-(1<<k)+1][k]).i;
}
$tarjan $
- 时间(\(total\))：\(O(n+m)\)
- 空间：\(O(n+m)\)
- 预处理：无
- \(underline\)
namespace TarjanLca{
//STL Warning!!!
struct Query{
int to,ord;
Query(int to=0,int ord=0):to(to),ord(ord){};
};
vector<Query> Q[MAXN];int prt[MAXN];
int father[MAXN];bool check[MAXN];
int find(int x){
return x==father[x]?x:father[x]=find(father[x]);
}
#define v e[i].to
void tarjan(int u,int fa){
father[u]=u;
edge(u) (v!=fa)&&(tarjan(v,u),1);check[u]=1;
for(vector<Query>::iterator it=Q[u].begin();it!=Q[u].end();++it){
int to=(*it).to,ord=(*it).ord;
(check[to])&&(prt[ord]=find(to));
}
father[u]=fa;
}
#undef v
int main(){
register int i;
n=read(),m=read();root=read();
BuildGraph(n-1);
for(i=1;i<=m;++i){
int u=read(),v=read();
Q[u].push_back(Query(v,i));Q[v].push_back(Query(u,i));
}
tarjan(root,root);
for(i=1;i<=m;++i) printf("%d\n",prt[i]);
return 0;
}
}
第三节 强联通分量和双联通分量
全是\(tarjan\)
缩点
-
强联通分量和双连通分量都能缩，区别不大。
-
注意到变量名别用什么\(~time~\)或者\(~hash\)。 欧阳老师的std就用了hash。
【模板】缩点
就缩点+\(DAG\)上找最长路
int dfn[N],low[N],lead,belong[N],cnt;//dfn[u] 到达u点的时间戳，low[u] u这个点能到达的时间戳最早的点
bool instk[N];//是否在栈里面
stack<int>s;
void dfs(int u) {
dfn[u]=low[u]=++lead;
instk[u]=1; s.push(u);
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(!dfn[v]) {
dfs(v);
low[u]=min(low[u],low[v]);
}
else if(instk[v]) {
low[u]=min(low[u],dfn[v]);
}
}
if(low[u]==dfn[u]) { //说明u点是u所在强连通分量中时间戳最早的那个点
++cnt;
int y=0;
while(y!=u) {//栈顶到u点这一chuoer点都属于一个强联通分量
y=s.top();
s.pop();
instk[y]=0;
belong[y]=cnt;
}
}
}
割顶和割边
【模板】割点（割顶）
int dfn[N],low[N],lead,RT,ans;
bool cut[N];//是不是割点
void dfs(int u,int fa) {
dfn[u]=low[u]=++lead;
int son=0;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v==fa)continue;
if(!dfn[v]) {
++son;//其实这里的儿子是互不连通的儿子数
dfs(v,u);
if(((RT==u&&son>1)||(RT!=u&&low[v]>=dfn[u]))&&(!cut[u])) {
++ans;
cut[u]=1;
}//判断是不是割点，每次开始的起点要特判
low[u]=min(low[u],low[v]);
}
else low[u]=min(low[u],dfn[v]);
}
}
桥
没有找到裸题
int dfn[N],low[N],lead,RT,ans;
bool cut[N];//是不是割边
void dfs(int u,int fa) {
dfn[u]=low[u]=++lead;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v==fa)continue;
if(!dfn[v]) {
dfs(v,u);
if(low[v]>low[u])cnt[i]=1;//就完了
low[u]=min(low[u],low[v]);
}
else low[u]=min(low[u],dfn[v]);
}
}
\(2-SAT\)
用来解决一些逻辑问题
将一个\(~bool~\)变量拆成两个点，\(~false~\)和\(~true~\)。
规定：对于变量\(~p~\)，
\(~p~\)表示\(~true~\),\(\lnot~p~\)表示\(~false~\)，
\(-->~\)是连有向边的意思。
则，
- \(~p~\)或者\(~q~\)：\(\lnot~p-->q~;~\lnot~q-->q\);
- 非\(~p~\)或者非\(~q~\)：\(p-->\lnot~q~;~q-->\lnot~q\);
- 非\(~p~\)或者\(~q~\)：\(~p-->q~;~\lnot~q-->\lnot~q\);
- \(~p~\)或者非\(~q~\)：\(\lnot~p-->\lnot~q~;~q-->~q\);
现推就行了，不满足一个，就必须满足另一个。
P4782 【模板】2-SAT 问题
int main() {
n=read();m=read();
for(int i=1;i<=m;++i) {
int u=read(),fu=read(),v=read(),fv=read();
add(u+(fu^1)*n,v+fv*n);//u不满足v满足
add(v+(fv^1)*n,u+fu*n);//v不满足u满足
//有向边
}
for(int i=1;i<=2*n;++i)//注意是2*n
if(!dfn[i])dfs(i); //缩点
for(int i=1;i<=n;++i) {
if(belong[i]==belong[i+n]) {//第i个bool变量满足false还要满足true
printf("IMPOSSIBLE");
return 0;
}
}
printf("POSSIBLE\n");
for(int i=1;i<=n;++i) {
if(belong[i]<belong[i+n])printf("0 ");
else printf("1 ");
}
return 0;
}
对于方案输出，
首先对于一个每一个强连通分量，它是一个满足局部的解。
那么怎样得到整体解呢？
我们可以知道将缩点后的图的拓扑排序后，
先确定拓扑序大的，它对拓扑序小的没有影响，
但如果先确定拓扑序小的，它可能导致拓扑序大的产生一系列反应而导致矛盾。
所以对于一个布尔变量\(~p~\)取，
当\(~true~\)点的拓扑序大于\(~false~\)点拓扑序时就取\(~true~\)，反之。
我们注意到，对于\(~tarjan~\)，
因为那个递归，
编号小的强联通分量拓扑序大，所以有了上面的代码。
第四节 最小生成树
\(Kruskal\)
- \(O(m\log m)\)
- 模板题 220ms
#include<bits/stdc++.h>
using namespace std;
const int N=5005,M=2e5+5;
int n,m,u[M],v[M],w[M],id[M],fa[N];
bool cmp(int x,int y) { return w[x]<w[y]; }
int find(int x) { return x==fa[x]?x:fa[x]=find(fa[x]); }
void Kruskal() {
int cnt=0,ans=0;
for(int i=1;i<=m;i++) {
int x=find(u[id[i]]),y=find(v[id[i]]);
if(x^y) cnt++,ans+=w[id[i]],fa[y]=x;
if(cnt==n-1) { printf("%d\n",ans); return; }
}
printf("orz\n");
}
int main() {
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++) fa[i]=i;
for(int i=1;i<=m;i++) scanf("%d%d%d",&u[i],&v[i],&w[i]),id[i]=i;
sort(id+1,id+1+m,cmp);
Kruskal();
return 0;
}
\(Prim\)
- \(O(n^2)\)
- 模板题 1.10s
void Prim() {
memset(dis, 0x3f,sizeof(dis)),memset(g,0x3f,sizeof(g));
dis[1]=0;
for(int i=1;i<=n;i++) {
int u=0;
for(int j=1;j<=n;j++) if(dis[j]<dis[u]&&!vis[j]) u=j;
vis[u]=1,sum+=dis[u],cnt++;
for(int j=1;j<=n;j++) if(g[u][j]&&!vis[j])
dis[j]=min(dis[j],g[u][j]);
}
if(cnt!=n) printf("orz\n");
else printf("%d\n",sum);
}
- 堆优化
- 模板\(330ms\)
priority_queue< pair<int,int> >q;
void Prim() {
dis[1]=0;
q.push(make_pair(0,1));
while(!q.empty()) {
int u=q.top().second;q.pop();
if(vis[u])continue;
vis[u]=1;
sum+=dis[u];
++cnt;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(dis[v]>e[i].w&&!vis[v]) {
dis[v]=e[i].w;
q.push(make_pair(-dis[v],v));
}
}
}
if(cnt!=n) printf("orz\n");
else printf("%d\n",sum);
}
int main() {
memset(dis, 0x3f, sizeof(dis));
scanf("%d%d",&n,&m);
for(int i=1,u,v,w;i<=m;i++) {
scanf("%d%d%d",&u,&v,&w);
if(!g[u][v])add(u,v,w);
else e[g[u][v]].w=min(e[g[u][v]].w,w);
if(!g[v][u])add(v,u,w);
else e[g[v][u]].w=min(e[g[v][u]].w,w);//处理一下重边
}
Prim();
return 0;
}
第五节 二分图匹配
匈牙利算法
- \(O( 跑不满 )\)
- 使用时间戳优化
- 模板题 \(3ms\)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
int n,m,e;
struct Edge { int v,nxt,w; } edge[N];
int head[N],k;
int bel[N],vis[N],ans,tim;
void add(int u,int v) {
edge[++k].v=v,edge[k].nxt=head[u],head[u]=k;
}
bool dfs(int u) {
for(int i=head[u];i;i=edge[i].nxt) {
int v=edge[i].v;
if(vis[v]==tim) continue;
vis[v]=tim;
if(!bel[v]||dfs(bel[v])) {
bel[v]=u;
return 1;
}
}
return 0;
}
int main() {
scanf("%d%d%d",&n,&m,&e);
for(int i=1,x,y;i<=e;i++) scanf("%d%d",&x,&y),add(x,y);
for(int i=1;i<=n;i++) tim=i,ans+=dfs(i);
printf("%d\n",ans);
return 0;
}
