字符串模板总结
\(I/O\)
读入一个字符:
scanf("%c",c);
cin>>c;
c=getchar();
读入一个字符串:
scanf("%s",s);
cin>>s;
fgets(s,len,stdin); //读入一行,不要用gets
scanf("%s",s+1); //下标从1开始
输出一个字符:
printf("%c",c);
cout<<c;
putchar(c);
输出一个字符串:
printf("%s",s);
cout<<s;
puts(s); //等价于printf("%s\n",s);
\(hash\)
把字符串有效地转化为一个整数。
单哈希版:
预处理\(1\)到\(n\)的前缀\(hash\)值:
for(int i=1;i<=n;++i)
ha[i]=(ha[i]*base+s[i])%mod;
取子串的\(hash\)值:
return (ha[r]-ha[l-1]*pw[r-l+1]+mod)%mod;
双哈希版:
预处理\(1\)到\(n\)的前缀\(hash\)值:
for(int i=1;i<=lena;i++)
for(int j=0;j<2;j++)
ha[i][j]=(ha[i-1][j]*base[j]+s[i])%mod[j];
取子串的\(hash\)值:
return make_pair((ha[r][0]-ha[l-1][0]*pw[r-l+1][0]+mod[0])%mod[0]
,(ha[r][1]-ha[l-1][1]*pw[r-l+1][1]+mod[1])%mod[1]);
自然上溢哈希:用\(unsigned\ int\)或\(unsigned\ long\ long\)。
\(hash\)素数的选择:
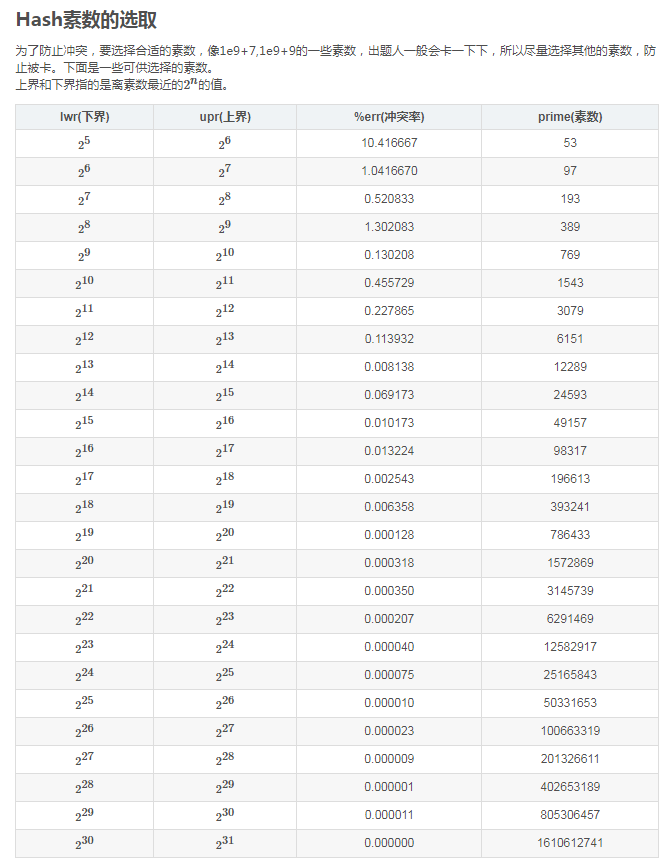
可以参考,也可以选择自己喜欢的质数。
\(Kmp\)
模板(下标从\(0\)开始):
void Get_next()
{
int i=0,j;
next[0]=j=-1;
while(i<len2)
{
if(j==-1||b[i]==b[j])
next[++i]=++j;
else j=next[j];
}
}
void Kmp()
{
int i=0,j=0;
while(i<len1)
{
if(j==-1||a[i]==b[j])
++i,++j;
else j=next[j];
if(j==len2)
{
printf("%d\n",i-len2+1);
j=next[j];
}
}
}
时间复杂度\(\Theta(|S_1|+|S_2|)\)
\(next\)数组的意义:
- 失配后的下一个匹配位置。
- 前缀的最长的\(border\)。
\(border\):定义一个字符串\(s\)的\(border\)为\(s\)的一个非\(s\)本身的子串\(t\),满足\(t\)既是\(s\)的前缀,又是\(s\)的后缀,即前缀后缀最大值。
注:如果下标从一开始,用\(next\)表示\(border\)长度的时候要减一。
应用:最小循环节:
给定一个字符串,询问还需要添加几个字符可以构成一个由n个循环节组成的字符串
可知我们应该先求出字符串的最小循环节的长度:假设字符串的长度为\(len\),那么最小的循环节就是\(cir = len-next[len] ;\) 如果有\(len\%cir == 0\),那么这个字符串就是已经是完美的字符串,不用添加任何字符;如果不是完美的那么需要添加的字符数就是\(cir - (len-(len/cir)*cir))\),相当于需要在最后一个循环节上面添加几个。
扩展\(Kmp\)
给定母串S,和子串T。
定义\(n=|S|,m=|T|,extend[i]=S[i..n]\)与T的最长公共前缀长度。请在线性的时间复杂度内,求出所有的\(extend[1..n]\)。
\(next\)数组意义:\(next[i]\)表示\(T[i..m]\)与\(T\)的最长公共前缀长度。
参考代码(下标从0开始):
void get_next()
{
int a=0,p=0;
nxt[0]=lent;
for(int i=1;i<lent;i++)
{
if(i+nxt[i-a]<p) nxt[i]=nxt[i-a];
else
{
if(i>=p) p=i;
while(p<lent&&t[p]==t[p-i]) p++;
nxt[i]=p-i;
a=i;
}
}
}
void get_extend()
{
int a=0,p=0;
for(int i=0;i<lens;i++)
{
if(i+nxt[i-a]<p) extend[i]=nxt[i-a];
else
{
if(i>=p) p=i;
while(p<lens&&s[p]==t[p-i]) p++;
extend[i]=p-i;
a=i;
}
}
}
时间复杂度\(\Theta(|S|+|T|)\)
\(Manacher\)
代码:
string s,a;
cin>>s;
a="$~";
int len=s.length();
for(int i=0;i<len;i++)
a+=s[i],a+="~";
int len2=a.length();
vector<int> p(len2+5,0);
int maxr=0,pos=0;
int ans=0;
for(int i=1;i<len2;i++)
{
p[i]= i<maxr ? min(p[2*pos-i],maxr-i) : 1;
while(a[i-p[i]]==a[i+p[i]]) p[i]++;
if(p[i]+i>maxr) maxr=p[i]+i,pos=i;
ans=max(ans,p[i]);
}
时间复杂度\(\Theta(n)\)
\(Trie\)
模板代码(下标从一开始):
void insert(char *a) //插入
{
int len=strlen(a),u=1;
for(int i=0;i<len;i++)
{
int c=a[i]-'a';
if(!tr[u][c]) tr[u][c]=++tot;
u=tr[u][c];++siz[u]; //siz表示子树中有几个串
}
book[u]=1;
++word[u]; //word表示当前点有几个字符串
}
int find(char *a) //查询a是否存在
{
int len=strlen(a),u=1;
for(int i=0;i<len;i++)
{
int c=a[i]-'a';
if(!tr[u][c]) return 0;
u=tr[u][c];
}
if(!book[u] return 0;
return 1;
}
void query(int u,int k) //查询字典序第k大,存到s数组中
{
if(word[u]>=k) return;
k-=word[u];
for(int c=0;c<26;++c)
if(tr[u][c])
{
if(k<=siz[tr[u][c]])
return s[++top]=c+'a',query(tr[u][c],k),void();
else k-=siz[tr[u][c]];
}
}
时间复杂度\(\Theta(\sum|S|)\)
\(01\text{Trie}\)处理异或
void insert(int x) //插入
{
int u=1; //注意根节点没有记录siz
for(int i=lim;~i;--i)
{
int s=x>>i&1;
if(!tr[u][s]) tr[u][s]=++cnt;
u=tr[u][s];++siz[u];
}
}
int query(int u,int v,int x) //找异或最大值
{
int res=0;
for(int i=lim;~i;--i)
{
int s=x>>i&1;
if(tr[u][s^1]) res|=(1<<i),u=tr[u][s^1];
else u=tr[u][s];
}
return res;
}
可持久化版本
void insert(int &now,int v,char *s) //插入
{
now=++cnt;int u=now,len=strlen(s+1);
memcpy(tr[u],tr[v],sizeof(tr[v]));
for(int i=1;i<=len;++i)
{
int c=s[i]-'a';
tr[u][c]=++cnt;u=tr[u][c];v=tr[v][c];
siz[u]=siz[v]+1;word[u]=word[v];
memcpy(tr[u],tr[v],sizeof(tr[v]));
}
++word[u];
}
//其他操作与普通版本几乎无区别
\(AC\)自动机
计算\(fail\)指针:
void Getfail() //fail指针
{
queue<int> que;
for(int i=0;i<26;i++)
if(tr[0][i]) que.push(tr[0][i]);
while(!que.empty())
{
int u=que.front();que.pop();
for(int i=0;i<26;i++)
{
int &v=tr[u][i];
if(v) fail[v]=tr[fail[u]][i],que.push(v);
else v=tr[fail[u]][i];
}
}
}
模板\(1\)(下文的变量意义与\(Trie\)中的基本一样):
给定\(n\)个模式串\(s_i\)和一个文本串\(t\),求有多少个不同的模式串在文本串里出现过。
两个模式串不同当且仅当他们编号不同。
代码:
void query(string s)
{
int u=0,ans=0,len=s.length();
for(int i=0;i<len;i++)
{
u=tr[u][s[i]-'a'];
for(int j=u;j&&word[j]!=-1;j=fail[j])
{
ans+=word[j];
word[j]=-1; //只找一遍
}
}
cout<<ans<<endl;
}
模板\(2\):
有\(N\)个由小写字母组成的模式串以及一个文本串\(T\)。每个模式串可能会在文本串中出现多次。你需要找出哪些模式串在文本串\(T\)中出现的次数最多。
代码:
void query(string s)
{
int u=0,ans=-1,len=s.length();
for(int i=0;i<len;i++)
{
u=tr[u][s[i]-'a'];
for(int j=u;j;j=fail[j])
vis[word[j]]++; //这里word的意义是该点对应串的编号
}
for(int i=1;i<=n;i++) ans=max(ans,vis[i]);
cout<<ans<<endl;
for(int i=1;i<=n;i++)、
if(vis[i]==ans) cout<<ss[i]<<endl;
}
模板\(3\):
给你一个文本串\(S\)和\(n\)个模式串\(T_{1..n}\),请你分别求出每个模式串\(T_i\)在\(S\)中出现的次数。
数据不保证任意两个模式串不相同。
代码(拓扑排序):
for(int i=0;i<len;i++)
{
int &v=tr[u][s[i]-'a'];
u=v?v:v=++tot;
}
if(!idx[u]) idx[u]=id; //在插入完后记一下每个点在原串中对应的id
else fa[id]=idx[u]; //如果有一个点对应多个id,就像并查集一样连一个fa
//记得fa要初始化为fa[i]=i
int &v=tr[u][i];
if(v) fail[v]=tr[fail[u]][i],que.push(v),++deg[fail[v]]; //在这里记录入度
else v=tr[fail[u]][i];
void query(string s)
{
queue<int> que;
int len=s.length(),u=0;
for(int i=0;i<len;i++)
vis[u=tr[u][s[i]-'a']]++;
//在fail树上跑拓扑排序
for(int i=1;i<=tot;i++)
if(!deg[i]) que.push(i);
while(!que.empty())
{
u=que.front();que.pop();
ans[idx[u]]=vis[u];
vis[fail[u]]+=vis[u]; //fail树上答案向上传递
deg[fail[u]]--;
if(!deg[fail[u]]) que.push(fail[u]);
}
}
后缀数组
void rsort()
{
for(int i=0;i<=m;++i) tax[i]=0;
for(int i=1;i<=n;++i) ++tax[rnk[i]];
for(int i=1;i<=m;++i) tax[i]+=tax[i-1];
for(int i=n;i>0;--i) sa[tax[rnk[tp[i]]]--]=tp[i];
}
void ssort()
{
rsort();
for(int w=1,p;p<n;m=p,w<<=1)
{
p=0;
for(int i=1;i<=w;++i) tp[++p]=n-w+i;
for(int i=1;i<=n;++i) if(sa[i]>w) tp[++p]=sa[i]-w;
rsort();
swap(tp,rnk);
rnk[sa[1]]=p=1;
for(int i=2;i<=n;++i)
rnk[sa[i]]=tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+w]==tp[sa[i-1]+w]?p:++p;
}
}
void Get_height() //height[i]=lcp(i,i-1),两个后缀的lcp为一段区间height的rmq
{
int p=0,j;
for(int i=1;i<=n;++i)
{
if(p) --p;
j=sa[rnk[i]-1];
while(a[i+p]==a[j+p]) ++p;
height[rnk[i]]=p;
}
}
后缀自动机
\(SAM\)模板
class SAM
{
private:
int link[maxn<<1],tr[maxn<<1][26];
int maxlen[maxn<<1],siz[maxn<<1],a[maxn<<1],las=1,cnt=1;
public:
void insert(int c)
{
int u=las,nu=las=++cnt;
siz[nu]=1;maxlen[nu]=maxlen[u]+1;
for(;u&&!tr[u][c];u=link[u]) tr[u][c]=nu;
if(!u) return link[nu]=1,void();
int v=tr[u][c];
if(maxlen[v]==maxlen[u]+1) return link[nu]=v,void();
int nv=++cnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=link[nu]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
}
void rsort(int x) //通常需要一遍基数排序求拓扑序
{
memset(tax,0,sizeof(tax));
for(int i=1;i<=cnt;++i) ++tax[maxlen[i]];
for(int i=1;i<=x;++i) tax[i]+=tax[i-1];
for(int i=cnt;i;--i) a[tax[maxlen[i]]--]=i;
}
};
广义\(SAM\)模板(在线版)(每插入一个串前把\(las\)设为一):
int insert(int c,int u)
{
if(tr[u][c])
{
int v=tr[u][c];
if(maxlen[u]+1==maxlen[v]) return v;
int nv=++scnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
return nv;
}
int nu=++scnt;
maxlen[nu]=maxlen[u]+1;
for(;u&&!tr[u][c];u=link[u]) tr[u][c]=nu;
if(!u) return link[nu]=1,nu;
int v=tr[u][c];
if(maxlen[u]+1==maxlen[v]) return link[nu]=v,nu;
int nv=++scnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=link[nu]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
return nu;
}
广义\(SAM\)模板(离线版):
struct Trie
{
int tr[maxn][26],cnt=1;
void insert(char *s)
{
int len=strlen(s+1),u=1;
for(int i=1;i<=len;++i)
{
int c=s[i]-'a';
u=tr[u][c]?tr[u][c]:tr[u][c]=++cnt;
}
}
}tt;
int insert(int c,int u)
{
int nu=++cnt;
maxlen[nu]=maxlen[u]+1;
for(;u&&!tr[u][c];u=link[u]) tr[u][c]=nu;
if(!u) return link[nu]=1,nu;
int v=tr[u][c];
if(maxlen[v]==maxlen[u]+1) return link[nu]=v,nu;
int nv=++cnt;
maxlen[nv]=maxlen[u]+1;link[nv]=link[v];link[v]=link[nu]=nv;
memcpy(tr[nv],tr[v],sizeof(tr[v]));
for(;u&&tr[u][c]==v;u=link[u]) tr[u][c]=nv;
return nu;
}
void bfs() //bfs建树
{
pos[1]=1;
que.push(1);
while(!que.empty())
{
int u=que.front();que.pop();
for(int i=0;i<26;++i)
if(tt.tr[u][i])
pos[tt.tr[u][i]]=insert(ipos[u]),que.push(tt.tr[u][i]);
}
}
应用:
求多个字符串的本质不同子串个数。
答案为:\(\sum maxlen[i]-maxlen[link[i]]\)
计算每个节点的\(endpos\)大小
注意上文插入的时候记录的\(siz\),基数排序后把\(siz\)往\(parent\)树上累加,最后每个点的\(siz\)即为\(endpos\)的大小。
for(int i=cnt;i;--i) siz[link[a[i]]]+=siz[a[i]];


