[数据结构] - 栈
栈的简介:
栈是一种特殊的线性表,特殊之处在于插入和删除操作的位置受到限制,若插入和删除操作只允许在线性表的一端进行,则是栈,特点是后进先出。
栈的抽象数据模型:
栈(stack) 是一种特殊的线性表,其插入和删除操作只允许在线性表的一端进行,允许操作的一端称为 栈顶(top)不允许操作的一端称谓栈底(Bottom),栈中插入元素操作称为 入栈(push),删除元素的操作称为出栈(pop),没有元素的栈称为空栈、
例如对数据序列{A,B,C,D}执行操作序列{入栈,出栈,入栈,入栈,出栈,出栈。出栈},出栈序列为{B,D,C,A}栈机器状态如图:

由于栈的插入和删除操作只允许在栈顶进行,每次入栈元素即成为栈顶元素,每次出栈元素总是最后一个入栈元素,因此栈的特点是后进先出(Last In First Out),就像一落盘子,每次将只有一个盘子在最上面,从最上面取走一个盘子,不能从中间插入或者插出。
栈的基本操作有创建栈,判断是否为空,入栈,出栈,和取出栈顶元素等。栈不支持对指定位置的插入,删除等。
顺序栈
采用顺序存储结构的栈称为顺序栈{Sequential Stack},声明顺序栈如下,实现栈接口,使用顺序表作为成员变量实现栈,约定null不能入栈。
其中,入栈和出栈操作实现为顺序表尾部插入和尾部删除,时间复杂度为O(1),顺序表的插入方法已经实现自动扩充数组容量,当需要扩充容量时,入栈的时间复杂度为 O(n)
栈和线性表是不同的数据抽象类型,栈概念不依赖于线性表而存在,我们只是使用顺序表进行设计,也可以使用数组实现。
链式栈
采用连式存储结构的栈称为链式栈(Linked Stack),单链表结构的链式栈及入栈,出栈操作如图,设单链表(不带头节点)头指针top指向第一个元素节点(栈顶),入栈操作是头插入,在栈顶节点之前插入节点,出栈操作是头删除,删除栈顶节点并返回栈顶元素,再使top指向新的栈顶节点。
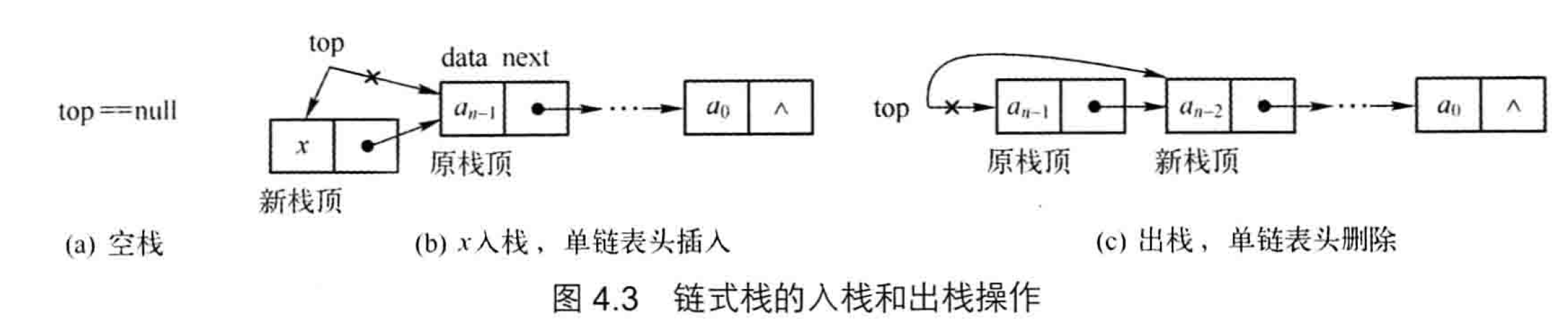
声明链式栈类如下,实现栈接口。使用单链表作为成员变量实现栈。入栈和出栈操作实现为单链表头部插入和删除。时间复杂度为O(1).
栈的应用
在实现嵌套调用或者递归调用,实现非线性结构的深度遍历算法、以非递归方式实现递归算法等软件系统设计中,栈都是必不可少的数据结构。
1.栈是嵌套调用机制的实现基础
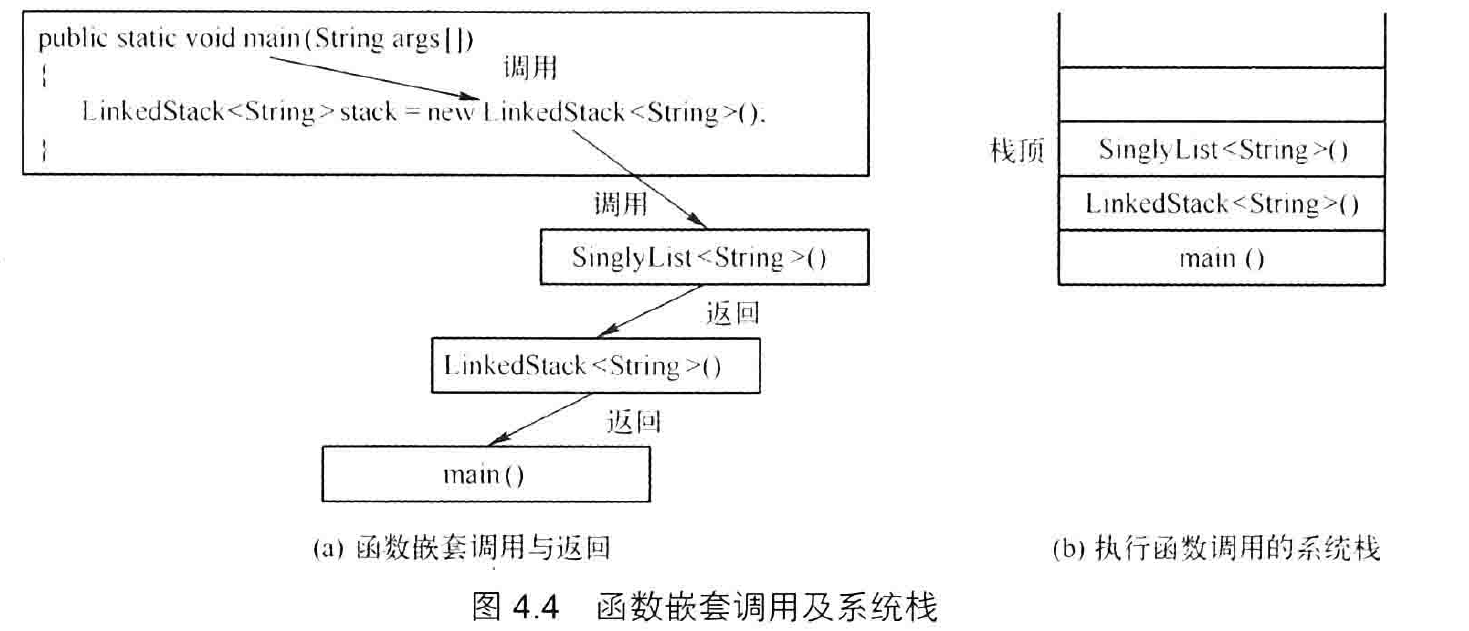
在一个函数体重调用另一个函数,称为函数的嵌套调用,例如,在 main() 函数中调用 LinkedStack<T>(), 在LinkedStack<T>()中调用SinglyList<T>(), 此时 3 个函数均在执行,仍然占用系统资资源。根据嵌套调用规则,每个函数在执行完后返回调用语句。那么,操作系统怎样做到返回调用的函数?他是如何知道该返回哪个函数?
由于函数返回次序与调用次序正好相反,如果借助一个栈“记住”函数从而来,就能获得函数返回的路径。当函数被调用时,操作系统将该函数的有关信息(地址,参数,局部变量值等)入栈,称为保护现场;一个函数执行完成返回后,出栈,获得调用函数信息,称为恢复现场,程序返回调用函数继续运行。
函数嵌套调用及系统栈如图,因此,栈是操作系统实现嵌套调用机制的基础。
实例:括号匹配语法检查:
程序中出现 () [] {} 都应该是左右匹配的,所谓括号匹配,是指一对左右括号不止要个数相等,而且必须先左后右依次出现,以此界定一个范围的起始和结束位置。 例如 () 是匹配的。 )( 是不匹配的,括号语法检查由编译器进行,如果不匹配则不能通过编译。编译器将给出错误信息。
括号可以嵌套,嵌套括号的原则是,一个右括号与其前面的一个最近的左括号匹配,因此检查括号是否匹配,需要一个栈,保存多个嵌套的左括号。
设infix是一个表达式字符串,从左向右依次对 infix 中的每个字符ch进行语法检查,若ch是左括号,则ch入栈,若ch是右括号,则出栈,若出栈字符为左括号,表示这一对括号匹配,若栈空或者出栈字符不是左括号,表示缺少与ch匹配 的左括号。
重复执行,当infix检查结束时,若栈空 ,则全部匹配正确。否则,栈中仍然有左括号,表示缺少右括号,
当infix = “((1+2)*3+4)” 判断括号匹配算法逻辑如图:
实例:使用栈计算算数表达式的值
将运算符写在两个操作数中间的表达式,叫做 中缀表达式(Infix Expression).中缀表达式中,运算符具有不同的优先级,还可以使用圆括号改变运算次序,这两点使得运算规则较复杂,求值过程不能直接从做导游按顺序的进行。
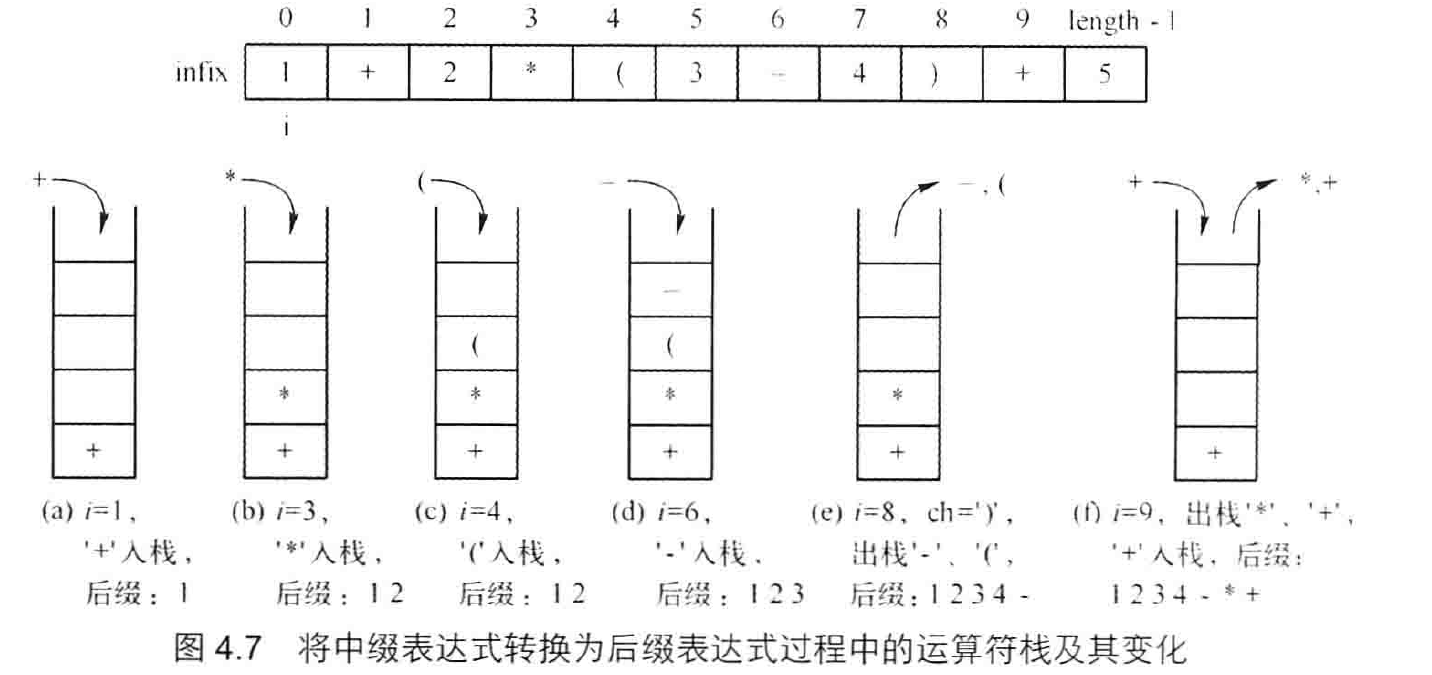
将运算符卸载两个操作数之前/后的表达式,分别称为 前/后缀表达式 (Prefix/Postfix Expression) 例如将中缀表达式 “1+2*(3-4)+5)” 转换为后缀表达式 1234 - * + 5+ 。后缀表达式中,运算符没有优先级,没有括号。求职过程能够严格从左到右按照顺序的进行,遇到运算符时,对他前面的两个操作数进行求值。符合运算器的求值规律。
1.将中缀表达式转换为后缀表达式
运算符优先级:(从低到高) ( + - * / )
对输入的中缀表达式从左到右遍历:
1)如果遇到数字,直接添加到后缀表达式末尾;
2)如果遇到运算符+、-、*、/:
先判断栈是否为空。若是,则直接将此运算符压入栈。若不是,则查看当前栈顶元素。若栈顶元素优先级大于或等于此操作符级别,则弹出栈顶元素,将栈顶元素添加到后缀表达式中,并继续进行上述判断。如果不满足上述判断或者栈为空,将这个运算符入栈。要注意的是,经过上述步骤,这个运算符最终一定会入栈。
3)如果遇到括号:
如果是左括号,直接入栈。如果是右括号,弹出栈中第一个左括号前所有的操作符,并将左括号弹出。(右括号别入栈)。
4)字符串遍历结束后,如果栈不为空,则弹出栈中所有元素,将它们添加到后缀表达式的末尾,直到栈为空。
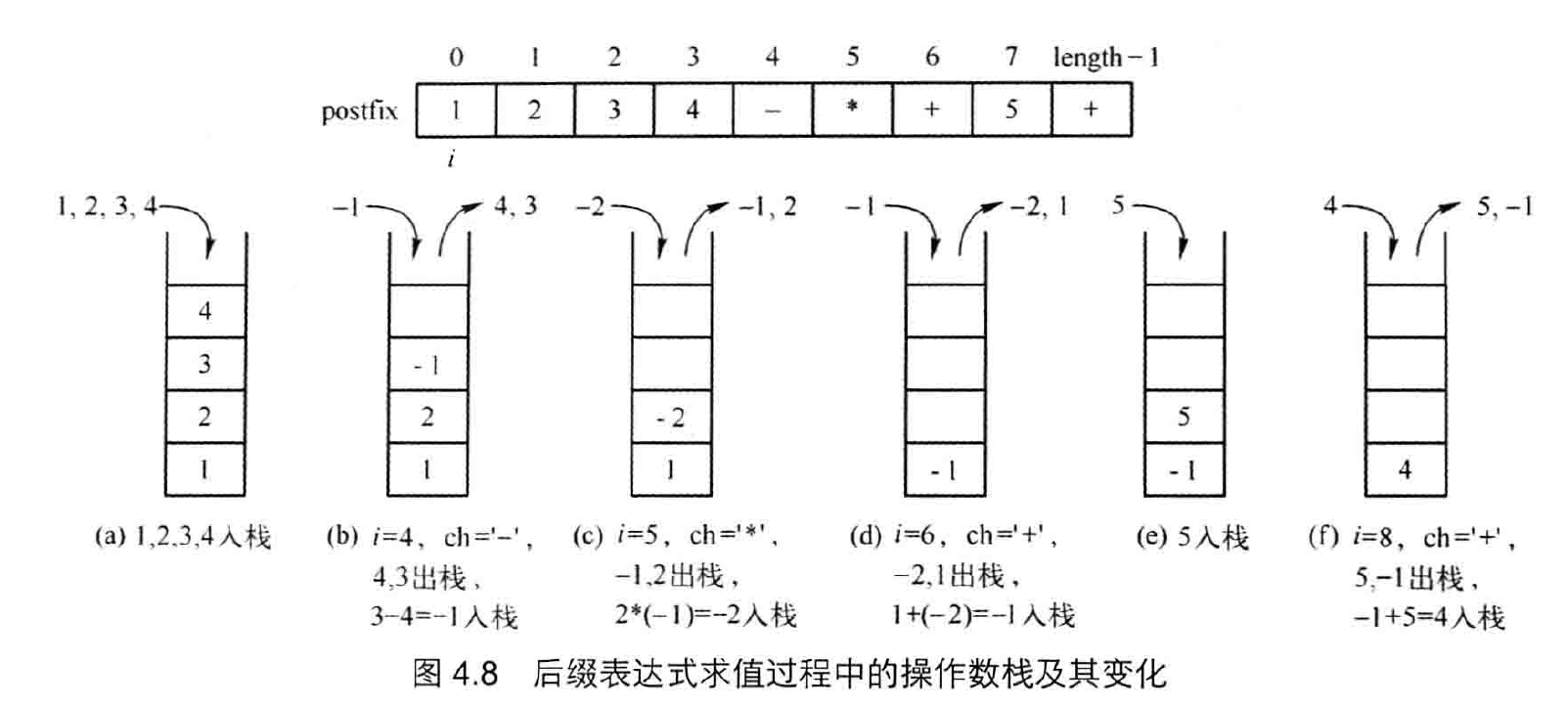
二、计算后缀表达式
后缀表达式的计算就相当简单了。准备一个数字栈。从左到右扫描后缀表达式,如果是数字,放入数字栈。如果是符号,从数字栈中弹出两个数字,第一个取出的数字为右运算数,第二个为左运算数,进行运算。然后将结果放进数字栈中。如此反复,直到读完整个表达式后,留在数字栈中的那个数字就是最终结果。