第五章学习小结
树和二叉树
定义概念不再赘述,需要注意的一些地方:
1.树的其他表示方式
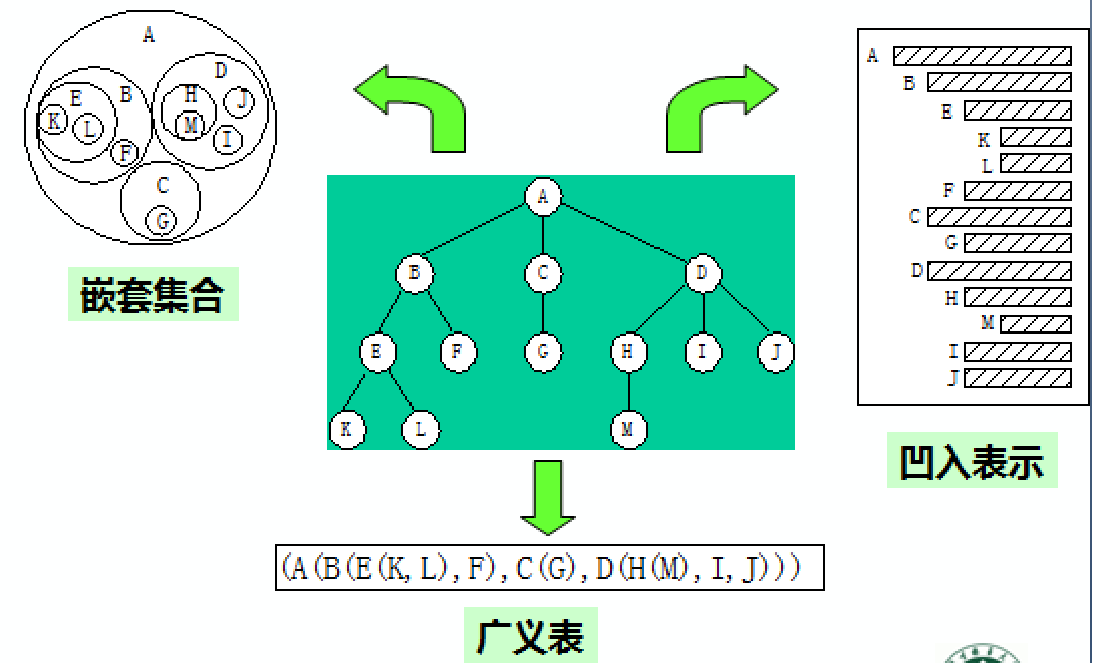
2.重点研究二叉树的原因
二叉树的结构最简单,规律性最强;
可以证明,所有树都能转为唯一对应的二叉树,不失一般性;
普通树转化为二叉树后,运算容易实现。
3.二叉树的性质
在二叉树的第i层上至多有2i-1个结点。
深度为k的二叉树上至多含2k - 1个结点(k≥1)。
对任何一棵二叉树,若它含有n0个叶子结点、n2个度为2的结点,则必存在关系式:n0 = n2 + 1。
具有n个结点的完全二叉树的深度为 (log2n) +1 。
对完全二叉树,若从上至下、从左至右编号,则编号为 i 的结点,其左孩子编号必为2i,其右孩子编号必为2i+1;其双亲的编号必为i/2。
4.森林与二叉树的互相转换
5.哈夫曼树的构造
在森林中选取两棵根结点权值最小的树作左右子树,构造一棵新的二叉树,置新二叉树根结点权值为其左右子树根结点权值之和。
在森林中删除这两棵树,同时将新得到的二叉树加入森林中。
重复上述两步,直到只含一棵树为止,这棵树即哈夫曼树。
习题
1.深入虎穴

1 #include<iostream> 2 #include<queue> 3 using namespace std; 4 5 typedef struct 6 { 7 int doors; //门的数量 8 int *p; // 指向具体门的编号,把p看作一个整型数组 9 }node; 10 11 int input(node *&a); 12 int find(node *a,int root); 13 14 int main() 15 { 16 //变量的定义 17 node *a; //定义一个动态整型数组 18 int root; 19 root=input(a); 20 cout<<find(a,root)<<endl; 21 22 return 0; 23 } 24 25 int input(node *&a) 26 { 27 int n,x,i,j,k; 28 bool *vi; 29 cin >> n; 30 a = new node[n+1]; //为a数组申请空间 31 vi= new bool[n+1]; //同上 32 for(i=1;i<=n;i++) //将vi数组初始化为false 33 { 34 vi[i]=false; 35 } 36 for(i=1;i<=n;++i) 37 { 38 cin>>x; 39 a[i].doors=x; 40 a[i].p=new int[x]; 41 for(j=0;j<x;++j) 42 { 43 cin>>a[i].p[j]; 44 vi[a[i].p[j]] =true; 45 } 46 } 47 for (k=1;k<=n;k++) //找出根在a数组的小标 48 { 49 if(!vi[k]) break; 50 51 } 52 return k; 53 } 54 int find(node *a,int root) 55 { 56 int x; 57 int i; 58 queue<int> q; //定义用于待访问的门编号的队列 59 q.push(root); 60 while(!q.empty()) 61 { 62 x=q.front(); 63 q.pop(); 64 for(i=0;i<a[x].doors;++i) 65 { 66 q.push(a[x].p[i]); 67 } 68 } 69 return x; 70 }
需要注意的是,题目并没有给出根节点,需要在循环体中找出根所在数组的下标;
老师还介绍了STL中队列的使用方法,可以省去建立队列的麻烦,但这并不代表我们不需要了解底层的实现方法;

1 #include<iostream> 2 using namespace std; 3 4 int n ; 5 bool jud[20]; 6 struct node{ 7 int lchild; 8 int rchild; 9 }tree[20]; //定义一个树的结构体; 10 int s[20]; //用来存树的信息; 11 int head = 0 , rear = 0; //用来输出叶子结点的序号; 12 int main() 13 { 14 cin>>n; 15 char l , r; 16 for(int i = 0 ; i < n ;i++) 17 { 18 cin>>l>>r; 19 if(l!='-') 20 { 21 tree[i].lchild = l - '0'; 22 jud[tree[i].lchild] = 1; //标记这个数字是i的左的孩子; 23 }else 24 { 25 tree[i].lchild = -1; //否则i没有左孩子,将其置为-1; 26 } 27 28 if(r!='-') 29 { 30 tree[i].rchild = r - '0'; 31 jud[tree[i].rchild] = 1; //标记这个数字是i的右的孩子; 32 }else 33 { 34 tree[i].rchild = -1; 35 } 36 } 37 int root; 38 for(int i = 0 ; i < n ;i++) 39 { 40 if(jud[i]==0) //如果i不是孩子,则它是根结点; 41 { 42 root = i ; 43 break; 44 } 45 } 46 int leaves = 0; 47 s[rear++] = root; 48 while(rear - head > 0 ) 49 { 50 int num = s[head++]; 51 if (tree[num].lchild == -1 && tree[num].rchild == -1) { //既没左孩子也没右孩子,输出叶节点; 52 53 if (leaves) 54 cout<<" "; 55 56 cout<<num; 57 58 ++leaves; //若是叶子结点,则叶子结点数目++; 59 60 } 61 62 if (tree[num].lchild != -1) { //如果存在,左孩子入队 63 64 s[rear++] = tree[num].lchild; 65 66 } 67 68 if (tree[num].rchild != -1) { //如果存在,右孩子入队 69 70 s[rear++] = tree[num].rchild; 71 72 } 73 74 75 } 76 return 0 ; 77 }
关键点:找到根结点,它不是任意结点的孩子;
记录叶子节点的序号,便于输出;
建立额外的一个数组来处理树的信息;
3.树的同构
给定两棵树T1和T2。如果T1可以通过若干次左右孩子互换就变成T2,则我们称两棵树是“同构”的。例如图1给出的两棵树就是同构的,因为我们把其中一棵树的结点A、B、G的左右孩子互换后,就得到另外一棵树。而图2就不是同构的。
讲一下图1具体是怎样同构的:
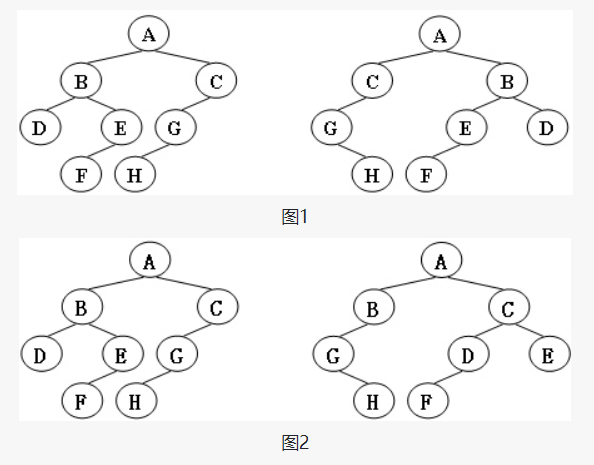
T1的A结点、B结点、G结点左右孩子互换,得到T2,因此图1是同构的;
判断是否同构的函数:

1 Status Isomprphic(int root1, int root2) 2 { 3 if( (root1 == -1) && (root2 == -1)) //都是空 ,同构 4 return OK; 5 if( (root1 == -1)&&(root2 != -1) || (root1 != -1)&&(root2 == -1))//其中一个为空,不同构 6 return ERROR; 7 if(T1[root1].data != T2[root2].data) //根不同,不同构 8 return ERROR; 9 if( (T1[root1].left == -1) && (T2[root2].left == -1) ) //左子树为空,则判断右子树 10 return Isomprphic(T1[root1].right, T2[root2].right); 11 12 if((T1[root1].left != -1) && (T2[root2].left != -1) &&( T1[T1[root1].left].data == T2[T2[root2].left].data) )//两树左子树皆不空,且值相等 13 return (Isomprphic(T1[root1].left, T2[root2].left) && Isomprphic(T1[root1].right, T2[root2].right) ); //判断其子树 14 15 else //两树左子树有一个空 或者 皆不空但值不等 16 return (Isomprphic(T1[root1].left, T2[root2].right) &&Isomprphic(T1[root1].right, T2[root2].left) ); //交换左右子树判断 17 18 19 }



