作业-AI数学基础

1,一座房子在过去20年里一共发生过2次被盗案,房子的主人养了一条狗,狗平均每周晚上叫3次,在盗贼入侵时狗叫的概率估计为0.9,请求:在狗叫的时候发生入侵的概率是多少?(计算过程写出了)?

解：

我们假设 A 事件为狗在晚上叫，B 为盗贼入侵，则

P(A) = 3 / 7，P(B)=2/(20·365)=2/7300，P(A | B) = 0.9，

按照公式得出结果:

P(B|A)=0.9*(2/7300)/(3/7)=0.00058

 

2,甲乙两个人赌博,假设两人获胜的概率相等,比赛规则是先胜三局者为赢家,可以获得100元的奖励.当比赛进行了三局的时候,其中甲胜了2局,乙胜了一局,这个时候由于某些原因中止了比赛,请问如何分配这100元才比较公平?

解：

甲获胜就有两种情况：1,甲赢了第四局，比赛结束；2,甲输掉了第四局而赢了第五局。于是有，概率P(甲)=1/2+(1/2)*(1/2)=3/4。而乙获胜的情况就只有一种，同时赢下第四局和第五局，那么，概率P(乙)=(1/2)*(1/2)=1/4。

因此，这100法郎就应该分给甲100*3/4=75元，分给乙100*1/4=25元。

 

3,有甲乙两个单位愿意聘用你,而你能够获得的信息如下,请根据工资待遇的差异情况,您选择哪家单位?为什么?

 

 

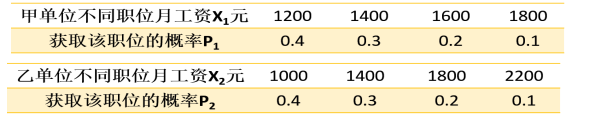
解：

根据月工资的分布列，可得

E(X1)=1200×0.4+1400×0.3+1600×0.2+1800×0.1=1400

D(X1)=（1200-1400）2×0.4+（1400-1400）2×0.3+（1600-1400）2×0.2+（1800-1400）2×0.1=40000

E(X2)=1000×0.4+1400×0.3+1800×0.2+2200×0.1=1400

D(X2)=（1000-1400）2×0.4+（1400-1400）2×0.3+（1800-1400）2×0.2+（2200-1400）2×0.1=112000

因为E(X1)=E(X2)，D(X1)＜D(X2)．

所以两家单位的月工资均值相等，

但甲单位不同职位的工资相对集中，乙单位不同职位的工资相对分散

因为我希望不同职位的工资差距小一些，就选择甲单位。

 

4,已知随机变量X的分布列如下, 分别求E(X),E(2X+5),D(X),的值.

 

 

解：

E(X)=－2×0.16＋1×0.44＋3×0.40=1.32，∴E(2X＋5)=2E(X)＋5=7.64

D(X)=(-2-1.32)2*0.16+(1-1.32)2*0.44+(3-1.32)2*0.4=2.9376

 σ(X)=1.7139

 

5,在n次独立重复试验中,设事件A发生的次数是X,且在每次试验中事件A发生的概率是p,那么事件A恰好发生k次的概率是为

 

 

 

 

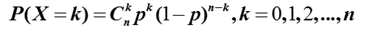
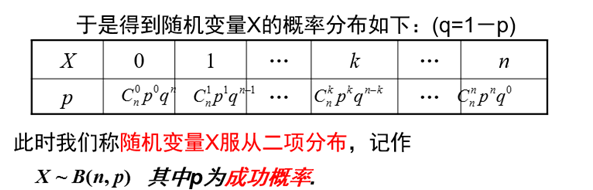
一名射手击中靶心的概率为0.9,如果他在同样的条件下连续的射击10次,求他击中靶心次数的均值和方差.

解：

E(X)=n*p =10*0.9=9

D(X)=(x₁-9)²*p₁+(x₂-9)²*p₂+(x₃-9)²*p₃+(x₄-9)²*p₄+(x₅-9)²*p₅+(x₆-9)²*p₆+(x₇-9)²*p₇+(x₈-9)²*p₈+(x₉-9)²*p₉+(x₁₀-9)²*p₁₀

 

6.在Python中实现图中函数并实现下图.

 

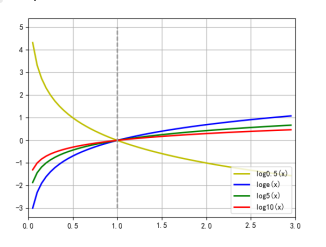
# -*- coding:utf-8 -*-
import math
import matplotlib.pyplot as plt
import numpy as np
x=np.arange(0.05,3,0.05)
plt.figure(figsize=(5,4))
y1=[math.log(a,0.5) for a in x]
plt.plot(x,y1,linewidth=2,color='y',label='log0.5(x)')
y2=[math.log(a,math.e) for a in x]
plt.plot(x,y2,linewidth=2,color='b',label='loge(x)')
y3=[math.log(a,5) for a in x]
plt.plot(x,y3,linewidth=2,color='g',label='log5(x)')
y4=[math.log(a,10) for a in x ]
plt.plot(x,y4,linewidth=2,color='r',label='log10(x)')

plt.legend(loc='lower right')
plt.grid(True)
plt.show()