文章目录
在学习A*算法之前,很好奇的是A*为什么叫做A*。在知乎上找到一个回答,大致意思是说,在A*算法之前有一种基于启发式探索的方法来提高Dijkstra算法的速度,这个算法叫做A1。后来的改进算法被称为A*。*这个符号是从统计文献中借鉴来的,用来表示相对一个旧有标准的最优估计。

启发式探索是利用问题拥有的启发信息来引导搜索,达到减少探索范围,降低问题复杂度的目的。
A*寻路算法就是启发式探索的一个典型实践,在寻路的过程中,给每个节点绑定了一个估计值(即启发式),在对节点的遍历过程中是采取估计值优先原则,估计值更优的节点会被优先遍历。所以估计函数的定义十分重要,显著影响算法效率。
A*算法描述
简化搜索区域
将待搜索的区域简化成一个个小方格,最终找到的路径就是一些小方格的组合。当然是可以划分成任意形状,甚至是精确到每一个像素点,这完全取决于你的游戏的需求。一般情况下划分成方格就可以满足我们的需求,同时也便于计算。
如下图区域,被简化成6*6的小方格。其中绿色表示起点,红色表示终点,黑色表示路障,不能通行。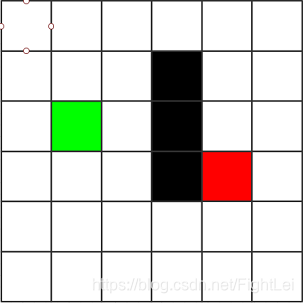
概述算法步骤
先描述A*算法的大致过程:
- 将初始节点放入到open列表中。
- 判断open列表。如果为空,则搜索失败。如果open列表中存在目标节点,则搜索成功。
- 从open列表中取出F值最小的节点作为当前节点,并将其加入到close列表中。
- 计算当前节点的相邻的所有可到达节点,生成一组子节点。对于每一个子节点:
- 如果该节点在close列表中,则丢弃它
- 如果该节点在open列表中,则检查其通过当前节点计算得到的F值是否更小,如果更小则更新其F值,并将其父节点设置为当前节点。
- 如果该节点不在open列表中,则将其加入到open列表,并计算F值,设置其父节点为当前节点。
- 转到2步骤
进一步解释
初始节点,目标节点,分别表示路径的起点和终点,相当于上图的绿色节点和红色节点
F值,就是前面提到的启发式,每个节点都会被绑定一个F值
F值是一个估计值,用F(n) = G(n) + H(n) 表示,其中G(n)表示由起点到节点n的预估消耗,H(n)表示节点n到终点的估计消耗。H(n)的计算方式有很多种,比如曼哈顿H(n) = x + y,或者欧几里得式H(n) = sqrt(x^2 + y^2)。本例中采用曼哈顿式。
F(n)就表示由起点经过n节点到达终点的总消耗
为了便于描述,本文在每个方格的左下角标注数字表示G(n),右下角数字表示H(n),左上方数字表示F(n)。具体如何计算请看下面的一个例子
具体寻路过程
接下来,我们严格按照A*算法找出从绿色节点到红色节点的最佳路径
首先将绿色节点加入到open列表中
接着判断open列表不为空(有起始节点),红色节点不在open列表中
然后从open列表中取出F值最小的节点,此时,open列表中只有绿色节点,所以将绿色节点取出,作为当前节点,并将其加入到close列表中
计算绿色节点的相邻节点(暂不考虑斜方向移动),如下图所示的所有灰色节点,并计算它们的F值。这些子节点既没有在open列表中,也没有在close列表中,所以都加入到open列表中,并设置它们的父节点为绿色节点
F值计算方式:
以绿色节点右边的灰色节点为例
G(n) = 1,从绿色节点移动到该节点,都只需要消耗1步
H(n) = 3,其移动到红色节点需要消耗横向2步,竖向一步,所以共消耗3步(曼哈顿式)
F(n) = 4 = G(n) + H(n)
试着算一下其他灰色节点的F值吧,看看与图上标注的是否一致
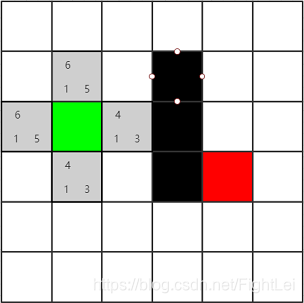
继续选择open列表中F值最小的节点,此时最小节点有两个,都为4。这种情况下选取哪一个都是一样的,不会影响搜索算法的效率。因为启发式相同。这个例子中按照右下左上的顺序选取(这样可以少画几张图(T▽T))。先选择绿色节点右边的节点为当前节点,并将其加入close列表。其相邻4个节点中,有1个是黑色节点不可达,绿色节点已经被加入close列表,还剩下上下两个相邻节点,分别计算其F值,并设置他们的父节点为黄色节点。

此时open列表中F值最小为4,继续选取下方节点,计算其相邻节点。其右侧是黑色节点,上方1号节点在close列表。下方节点是新扩展的。主要来看左侧节点,它已经在open列表中了。根据算法我们要重新计算它的F值,按经过2号节点计算G(n) = 3,H(n)不变,所以F(n) = 6相比于原值反而变大了,所以什么也不做。(后面的步骤中重新计算F值都不会更小,不再赘述)
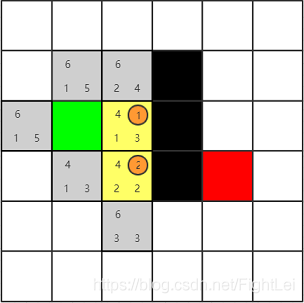
此时open列表中F值最小仍为4,继续选取
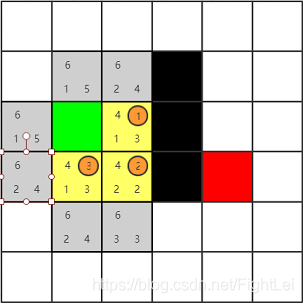
此时open列表中F值最小为6,优先选取下方节点
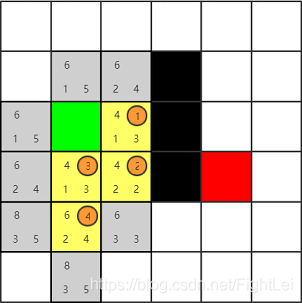
此时open列表中F值最小为6,优先选取右方节点

此时open列表中F值最小为6,优先选取右方节点
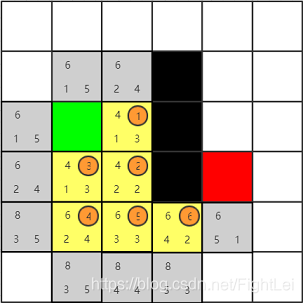
此时open列表中F值最小为6,优先选取右方节点
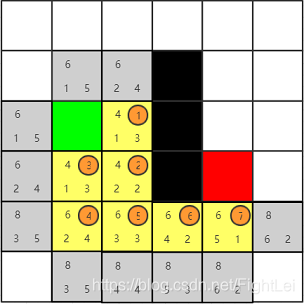
此时我们发现红色节点已经被添加到open列表中,算法结束。从红色节点开始逆推,其父节点为7号,7号父节点为6号,6号父节点为5号,5号父节点为2号(注意这里5号的父节点是2号,因为5号是被2号加入到open列表中的,且一直未被更新),2号父节点为1号,最终得到检索路径为:绿色-1-2-5-6-7-红色
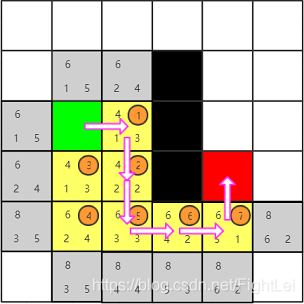
模拟需要更新F值的情况
在上面的例子中,所有遇到已经在open列表中的节点重新计算F值都不会更小,无法做更新操作。
所以再举一个例子来演示这种情况。相同的搜索区域,假设竖向或横向移动需要消耗1,这次也支持斜方向移动了,但是斜方向可能都是些山路不好走,移动一次需要消耗4。对应的相邻节点F值如下图所示
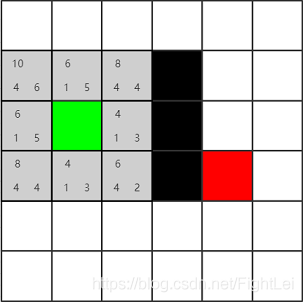
同样选择open列表中F值最小的节点,我们优先选择了右方节点,计算其相邻节点。共8个。其中三个是黑色节点,一个绿色节点在close列表中,不考虑。上方两个和下方两个都是已经在open列表中了,要重新计算F值。
先看左上角的相邻节点,通过黄色节点到达该节点,G(n) = 5,H(n)不变,F(n)反而更大了,所以什么也不做。左下角节点同理。
上方居中节点,通过黄色节点计算G(n) = 2, H(n)不变,F(n) = 6 < 8 所以,更新这个节点的F值,并将其父节点修改为黄色节点。下方居中节点同理。
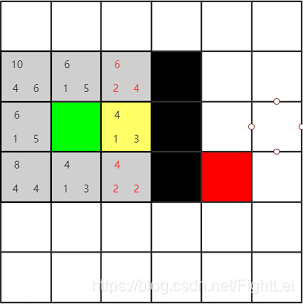
Lua代码实现
写了一套A*算法的Lua实现。主要特点如下:
-
优化效率,采用了map缓存,避免多次循环遍历
-
支持配置移动权重
-
支持配置是否可以斜向移动,斜向时墙角是否可通行
源码请查看:https://github.com/iwiniwin/ResourceLibrary/blob/master/lua/AStar.lua



