数据结构和算法：基础排序算法（Python）

基础排序算法虽然在实际开发中很少用到，但是在面试的时候却有很大概率被问到，可能不会要你现场写一个排序算法，但通常会问你某种算法的原理或者排序方法，所以在这里重新整理一下一些基础的排序算法，包括：冒泡排序，插入排序，选择排序，希尔排序，快速排序，归并排序，堆排序，基数排序。

1. 冒泡排序

原理

每次遍历找到其中的最大值：从左到右遍历全部n个元素，每次比较相邻两个元素的大小，将较大的一个放到右边（“冒泡”），直到第n-1个元素与第n个元素的比较后，整个序列的最大元素就“冒泡”到了最后，接着以同样的方法重新遍历第1个元素到n-1个元素，找出这n-1个元素中最大的元素，并“冒泡”到最后的位置。这样多次遍历后就形成了一个从左到右升序的序列。

示例代码

"""冒泡排序"""
import random


def bubble_sort(array):
    for i in range(len(array) - 1):
        for j in range(len(array) - 1 - i):
            if array[j] > array[j+1]:
                array[j], array[j+1] = array[j+1], array[j]


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    bubble_sort(random_array)
    print(f'After sorted: {random_array}')

Before sorted: [65, 36, 12, 18, 28, 65, 82, 93, 89, 79]
After sorted: [12, 18, 28, 36, 65, 65, 79, 82, 89, 93]

2. 插入排序

原理

将一个元素插入到一个已排好序的序列中：将第1个元素和第2个元素进行比较，将较大的元素放到右边，这样就有了一个有2个元素的已排好序（升序）的序列，接着将第3个元素依次与它前面的第2个和第1个元素进行比较，并插入到合适的位置，这样就成了一个有3个元素的已排好序（升序）的序列，以此类推，直到将最后一个元素也插入到前面已排好序的序列中时，就形成了一个升序的序列。

示例代码

import random


def insertion_sort(array):
    for i in range(1, len(array)):
        for j in range(i, 0, -1):
            if array[j] < array[j-1]:
                array[j-1], array[j] = array[j], array[j-1]


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    insertion_sort(random_array)
    print(f'After sorted: {random_array}')

Before sorted: [95, 17, 19, 19, 83, 88, 55, 65, 45, 7]
After sorted: [7, 17, 19, 19, 45, 55, 65, 83, 88, 95]

3. 选择排序

原理

选择序列中的最小值和序列最前面的元素交换位置：第一次遍历第0到第n个元素，找到最小值后（如果该最小值不是第0个元素），就将该元素和第0个元素互换位置，如此之后第0个元素就是序列中值最小的元素了，接下来遍历第1到第n个元素，找到最小值后（如果该最小值不是第1个元素），就将该元素和第1个元素互换位置，如此之后第0个元素和第1个元素组成的序列就是一个升序的序列了，以此类推，将后面的元素都遍历完后，整个序列就变成一个升序的序列了。

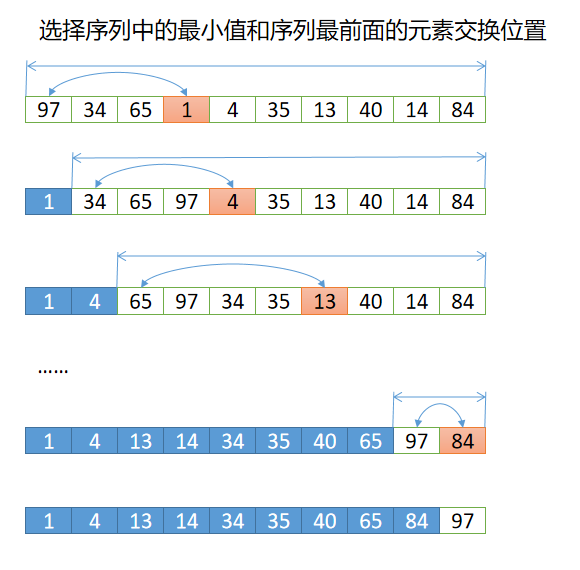
示例代码

import random


def select_sort(array):
    for i in range(0, len(array) - 1):
        min_index = i
        for j in range(i + 1, len(array)):
            if array[j] < array[min_index]:
                min_index = j

        if i != min_index:
            array[i], array[min_index] = array[min_index], array[i]


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    select_sort(random_array)
    print(f'After sorted: {random_array}')

Before sorted: [97, 34, 65, 1, 4, 35, 13, 40, 14, 84]
After sorted: [1, 4, 13, 14, 34, 35, 40, 65, 84, 97]

4. 希尔排序

原理

希尔排序其实也是一种插入排序，是本文介绍的第2种简单插入排序的改进版本，在希尔排序中，“段”（也叫增量）的概念很重要：每次遍历序列时将序列分成等长的“段”，遍历完成后保证在每段中相同位置的元素都满足前一段的元素小于后一段的元素，相当于每段中相同位置的元素就构成了一个升序的序列了，段的长度按照 step = len(array) // 2; step //= 2 分割，直到最后step为1时，也满足每个段的相同位置，前一段的元素都小于后一段的元素，因为每段序列中就只有1个元素，所以此序列就自然而然变成了一个升序的序列。

示例代码

import random


def shell_sort(array):
    step = len(array) // 2
    while step > 0:
        # 从最后一段step开始往前遍历
        for i in range(step, len(array)):
            value = array[i]
            # j表示前一段step的坐标
            j = i - step
            # 依次往前遍历每一段step，并把大于最后一段value的元素依次往后挪
            while j >= 0 and array[j] > value:
                array[j+step] = array[j]
                j -= step
            array[j+step] = value
        step //= 2


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    shell_sort(random_array)
    print(f'After sorted: {random_array}')

Before sorted: [51, 84, 42, 56, 65, 61, 25, 1, 29, 40]
After sorted: [1, 25, 29, 40, 42, 51, 56, 61, 65, 84]

5. 快速排序

原理

选取一个元素（通常就是序列最前端的那个元素），将其他比它小的元素放都到该元素前面，比它大的元素都放到该元素后面，这样下来，以该元素为中心点的“前”、“中”、“后”就形成了一个升序的序列，再以递归的方式将该中心点两边的序列以同样的方式进行“排序”，最后得到的序列整体就自然而然变成一个升序的序列了。

示例代码

import random


def quick_sort(array, low, high):
    if low >= high:
        return

    pivot_index = low
    pivot = array[pivot_index]
    for i in range(low + 1, high + 1):
        if array[i] < pivot:
            pivot_index += 1
            array[i], array[pivot_index] = array[pivot_index], array[i]

    array[low], array[pivot_index] = array[pivot_index], array[low]

    quick_sort(array, low, pivot_index - 1)
    quick_sort(array, pivot_index + 1, high)


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    quick_sort(random_array, 0, len(random_array) - 1)
    print(f'After sorted: {random_array}')

Before sorted: [18, 45, 50, 20, 84, 28, 51, 29, 87, 86]
After sorted: [18, 20, 28, 29, 45, 50, 51, 84, 86, 87]

6. 归并排序

原理

分治策略（分而治之）：使用 二分法 和 递归 不断将序列进行分割，直至分割到最小片段（只有两个元素），然后对二分后的两个片段进行排序，排好序之后再回到递归的上一层进行重复的操作即可（每一次递归只是片段的位置或长度不同而已，操作方法都是一样的）。

示例代码

import random


def merge_sort(array, low, high):
    """使用二分法将序列不断进行分割，直至分割为最小片段（只有两个元素）,
    然后将片段进行排序"""
    mid = (low + high) // 2
    if low < high:
        merge_sort(array, low, mid)
        merge_sort(array, mid + 1, high)
        merge(array, low, mid, high)

        # 这里只是为了更直观的展示排序过程，如果有需要，可以添加打印mid的值
        print(low, high, array)

    return array


def merge(array, low, mid, high):
    """排序：以mid为分界点遍历并对比两边的值，然后形成一个有序的临时序列，
    最后再赋值回原序列"""
    temp_array = [None] * (high - low + 1)
    i = low
    j = mid + 1
    k = 0
    while i <= mid and j <= high:
        if array[i] < array[j]:
            temp_array[k] = array[i]
            k += 1
            i += 1
        else:
            temp_array[k] = array[j]
            k += 1
            j += 1

    # 将另一个片段中剩余的元素放入临时数组中
    # 下面的两个while，每次只会有一个被执行，因为前面的while中i或j一定会有一个达到上限
    while i <= mid:
        temp_array[k] = array[i]
        k += 1
        i += 1

    while j <= high:
        temp_array[k] = array[j]
        k += 1
        j += 1

    for x in range(len(temp_array)):
        array[x + low] = temp_array[x]


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    merge_sort(random_array, 0, len(random_array) - 1)
    print(f'After sorted: {random_array}')

Before sorted: [65, 77, 33, 17, 30, 26, 76, 41, 38, 85]
0 1 [65, 77, 33, 17, 30, 26, 76, 41, 38, 85]
0 2 [33, 65, 77, 17, 30, 26, 76, 41, 38, 85]
3 4 [33, 65, 77, 17, 30, 26, 76, 41, 38, 85]
0 4 [17, 30, 33, 65, 77, 26, 76, 41, 38, 85]
5 6 [17, 30, 33, 65, 77, 26, 76, 41, 38, 85]
5 7 [17, 30, 33, 65, 77, 26, 41, 76, 38, 85]
8 9 [17, 30, 33, 65, 77, 26, 41, 76, 38, 85]
5 9 [17, 30, 33, 65, 77, 26, 38, 41, 76, 85]
0 9 [17, 26, 30, 33, 38, 41, 65, 76, 77, 85]
After sorted: [17, 26, 30, 33, 38, 41, 65, 76, 77, 85]

7. 堆排序

堆排序其实并不复杂，只要了解了对应的堆数据结构知识，代码其实就很简单了，不然光看代码是很难理解的，堆排序需要用到大顶堆或小顶堆的数据结构。

7.1 数组与堆

堆的定义：堆是一种完全二叉树的数据结构，若二叉树中每个节点的值都大于或等于其左右子节点的值，则称之为大顶堆，大顶堆的根节点为整个二叉树中的最大值；而相反，若二叉树中每个节点的值都小于或等于其左右子节点的值，则称之为小顶堆，小顶堆的根节点为整个二叉树中的最小值。

完全二叉树中编号为i的左子节点编号为 2i+1 ，右子节点的编号为 2i+2 ，所以用数组表示的堆应该满足：

array[i] >= array[2i+1] 且 array[i] >= array[2i+2]，即大顶堆

或

array[i] <= array[2i+1] 且 array[i] <= array[2i+2]，即小顶堆

7.2 堆排序

原理

以大顶堆为例：将一个数组构造成一个大顶堆之后，其根节点就是整个数组最大值（此时整个数组的最大元素已找出），然后将其与尾部元素（最后一个编号的节点）进行交换，然后将除了尾部元素的其他节点再次构造成一个新的大顶堆，那么这个新的大顶堆的根节点元素就是整个数组的第二大元素，然后再次将它与自己的尾部元素进行交换，以此类推，将所有堆的最大元素依次往后放，最后形成的就是一个升序的数组了。

示例代码

import random


def heap_sort(array):
    """使用大顶堆进行排序"""

    # 构造大顶堆：调整数组，使之符合大顶堆的数据结构
    for i in range(len(array) // 2 - 1, -1, -1):
        adjust(array, i, len(array))

    for i in range(len(array) - 1, -1, -1):
        # 将堆的根节点元素与堆的尾部元素交换
        array[0], array[i] = array[i], array[0]
        # 将除了尾部元素之外的元素作为新的堆进行调整，形成新的大顶堆
        adjust(array, 0, i)


def adjust(array, pos, length):
    """调整节点值，使之符合大顶堆的数据结构特点"""

    # 左子节点的下标
    child = pos * 2 + 1
    if child + 1 < length and array[child] < array[child + 1]:
        child += 1

    if child < length and array[pos] < array[child]:
        array[pos], array[child] = array[child], array[pos]
        # 继续调整其中一个子节点
        adjust(array, child, length)


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    heap_sort(random_array)
    print(f'After sorted: {random_array}')

Before sorted: [7, 91, 54, 42, 32, 43, 82, 81, 43, 2]
After sorted: [2, 7, 32, 42, 43, 43, 54, 81, 82, 91]

8. 基数排序

原理

核心思想：基数排序的思想其实很简单，大家平时可能都有想到过，只不过具体的实现方法（算法）可能没有基数排序这么好，其思想就是数字的位数越多，则这个数字就越大，如果位数相同，那么高位的数字越大，则这个数字就越大。是不是很简单！其实代码逻辑也不难，读一遍然后稍微想一下就可以懂了。

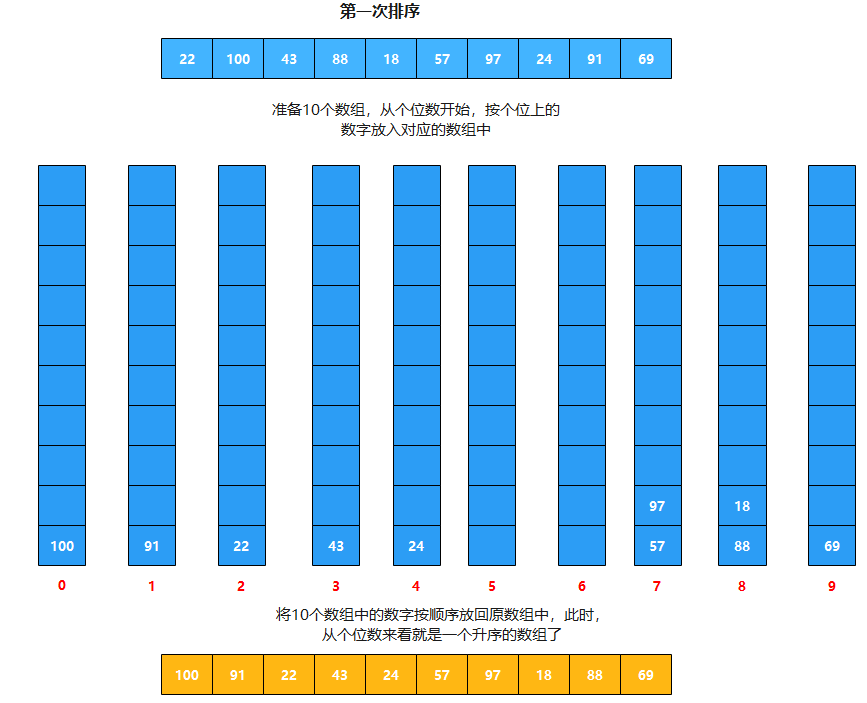
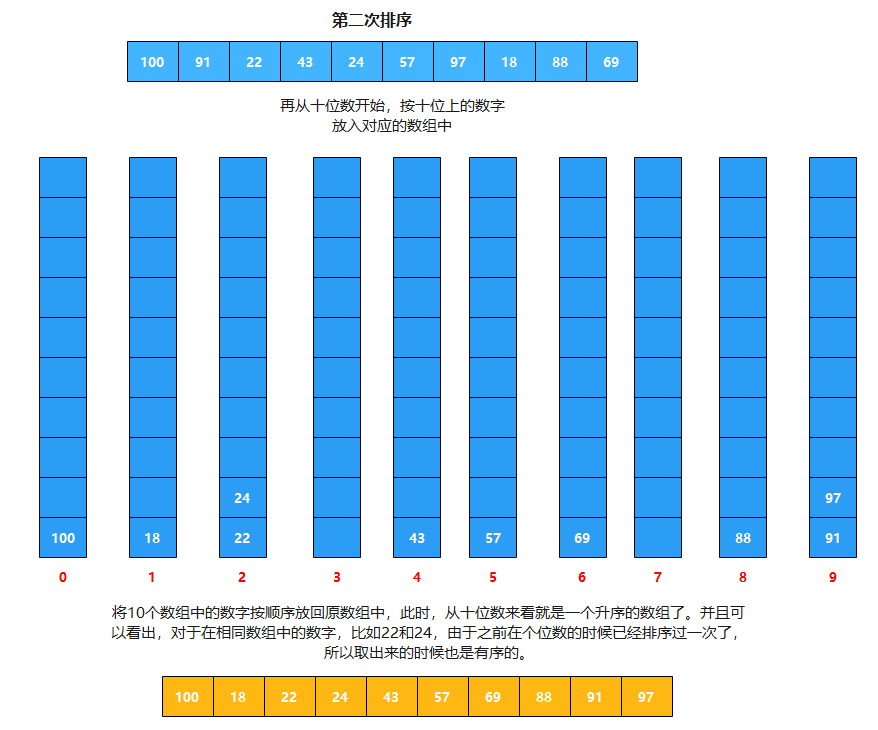
示例代码

import random


def basic_sort(array):
    # 找到数组中的最大值
    max_value = 0
    for i in range(len(array)):
        if array[i] > max_value:
            max_value = array[i]

    # 计算最大值的位数，也是之后要遍历计算的次数
    times = 0
    while max_value > 0:
        max_value //= 10
        times += 1

    arrays = [[] for _ in range(10)]
    for i in range(times):
        # 根据i位上的数字放入对应的子数组中
        for j in range(len(array)):
            x = array[j] % 10 ** (i + 1) // 10 ** i
            arrays[x].append(array[j])

        # 将子数组中的数字放回原数组array中，
        # 此时的array已是按i位的数字排好序了
        count = 0
        for sub_array_index in range(10):
            while len(arrays[sub_array_index]) > 0:
                array[count] = arrays[sub_array_index].pop(0)
                count += 1


if __name__ == '__main__':
    # 产生一个有10个元素的乱序的列表
    random_array = list(random.randint(1, 100) for _ in range(10))
    print(f'Before sorted: {random_array}')
    basic_sort(random_array)
    print(f'After sorted: {random_array}')

Before sorted: [22, 100, 43, 88, 18, 57, 97, 24, 91, 69]
After sorted: [18, 22, 24, 43, 57, 69, 88, 91, 97, 100]

注：各排序算法的时间复杂度和空间复杂度

表格图片来自https://blog.csdn.net/gane_cheng/article/details/52652705