go常规算法题

目录

• 二分查找
• 快排1
• 快排2
• 冒泡排序
• 遍历二叉树（前序，中序，后序）
• 涵洛塔
• 单链表
• 双链表
• 链表总结

二分查找

func binSearch(li []int, value, left, right int) int {
	mid := (left + right) / 2
	if li[mid] == value {
		return mid
	} else if li[mid] > value {
		//左边
		return binSearch(li, value, left, mid-1)
	} else {
		//右边
		return binSearch(li, value, mid+1, right)
	}
}

func TestBinSearch() {
	li := []int{1, 2, 3, 4, 5, 6, 7, 8, 9}
	target := 5
	left := 0
	right := len(li) - 1
	mid := binSearch(li, target, left, right)
	fmt.Println(mid)
}

快排1

func quickSort(li []int, left, right int) []int {
	if left < right {
		mid := partition(li, left, right)
		quickSort(li, left, mid-1)
		quickSort(li, mid+1, right)
	}
	return li
}

func partition(li []int, left, right int) int {
	tmp := li[left]
	for left < right {
		if li[right] >= tmp {
			right -= 1
		}
		li[left] = li[right]
		if li[left] <= tmp {
			left += 1
		}
		li[right] = li[left]
	}
	li[left] = tmp
	return left
}

func TestQuickSort() {
	li := []int{4, 3, 2, 1}
	Rli := quickSort(li, 0, len(li)-1)
	fmt.Println(Rli)
}

快排2

//快排
func quickSort(li []int, letf, right int) []int {
	for letf < right {
		if letf < right {
			if li[letf] > li[right] {
				li[right], li[letf] = li[letf], li[right]
				right--
			}
			if li[letf] < li[right] {
				letf++
			}
		}
	}
	fmt.Println(li)
	return li
}

func main() {
	li := []int{9, 8, 7, 6, 5, 4, 3, 2, 1}
	quickSort(li, 0, len(li)-1)
}

冒泡排序

//冒泡
func sort(li []int) {
	for i := 0; i < len(li); i++ {
		for k, v := range li {
			if k == len(li)-1 {
				break
			}
			if v > li[k+1] {
				li[k], li[k+1] = li[k+1], li[k]
			}
		}
	}
	fmt.Println(li)
}

func main() {
	li := []int{9, 8, 7, 6, 5, 4, 3, 2, 1}
	sort(li)
}

遍历二叉树（前序，中序，后序）

type Node struct {
	data   string // 节点
	lchild *Node  // 左孩子
	rchild *Node  // 右孩子
}

// 前序遍历
// ABDFGHIEC
func preOrder(a *Node) {
	if a != nil {
		print(a.data)
		preOrder(a.lchild)
		preOrder(a.rchild)
	}
}

// 中序遍历
// FDHGIBEAC
func inOrder(a *Node) {
	if a != nil {
		inOrder(a.lchild)
		print(a.data)
		inOrder(a.rchild)
	}
}

// 后序遍历
// FHIGDEBCA
func postOrder(a *Node) {
	if a != nil {
		postOrder(a.lchild)
		postOrder(a.rchild)
		print(a.data)
	}
}

func main() {
	a := Node{data: "A"}
	b := Node{data: "B"}
	c := Node{data: "C"}
	d := Node{data: "D"}
	e := Node{data: "E"}
	f := Node{data: "F"}
	g := Node{data: "G"}
	h := Node{data: "H"}
	i := Node{data: "I"}

	a.rchild = &c
	a.lchild = &b
	b.lchild = &d
	b.rchild = &e
	d.lchild = &f
	d.rchild = &g
	g.lchild = &h
	g.rchild = &i

	preOrder(&a)
}

涵洛塔

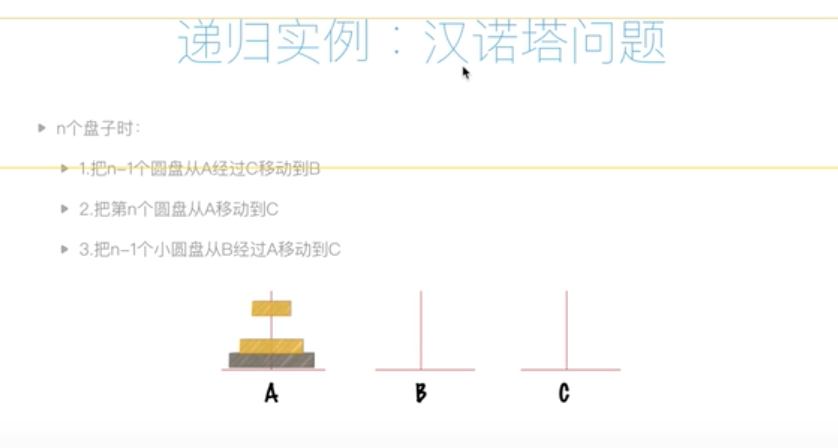
var num int

func hanoi(n int, a, b, c string) int {
	/*
		递归贝诺塔问题，abc三个棍子，目的：全部移动到另一更棍子
		    :param n: 盘子数
		    :param a: 棍子a
		    :param b: 棍子b
		    :param c: 棍子c
	*/
	if n > 0 {
		hanoi(n-1, a, c, b)
		num += 1
		hanoi(n-1, b, a, c)
	}
	return num
}

func TestHanoi() {
	num = hanoi(3, "A", "B", "c")
	fmt.Println(num)
}

单链表

创建单链表：

type node struct {
	data string
	next *node
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}
	a.next = &b
	b.next = &c

	fmt.Println(a.next.next.data) //c
	preNode(&a)
}

遍历单链表：

//遍历单链表
func preNode(t *node) {
	fmt.Println(t.data)
	if t.next != nil {
		preNode(t.next)
	}
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}
	a.next = &b
	b.next = &c

	preNode(&a)
}

单链表头部插入：

type node struct {
	data string
	next *node
}

//头部插入
func headerInto(t, d *node) *node {
	d.next = t
	return d
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}
	a.next = &b
	b.next = &c

	d := node{data: "d"}
	//在头部插入d节点
	H := headerInto(&a, &d)
	fmt.Println(H.data)
	fmt.Println(H.next.next.next.data)
}

单链表尾部插入：

type node struct {
	data string
	next *node
}
//尾部插入
func tailInto(t, d *node) *node {
	t.next = d
	return d
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}
	a.next = &b
	b.next = &c

	d := node{data: "d"}
	//在尾部插入d节点
	tailInto(&c, &d)

	fmt.Println(a.next.next.next.data) //d
}

双链表

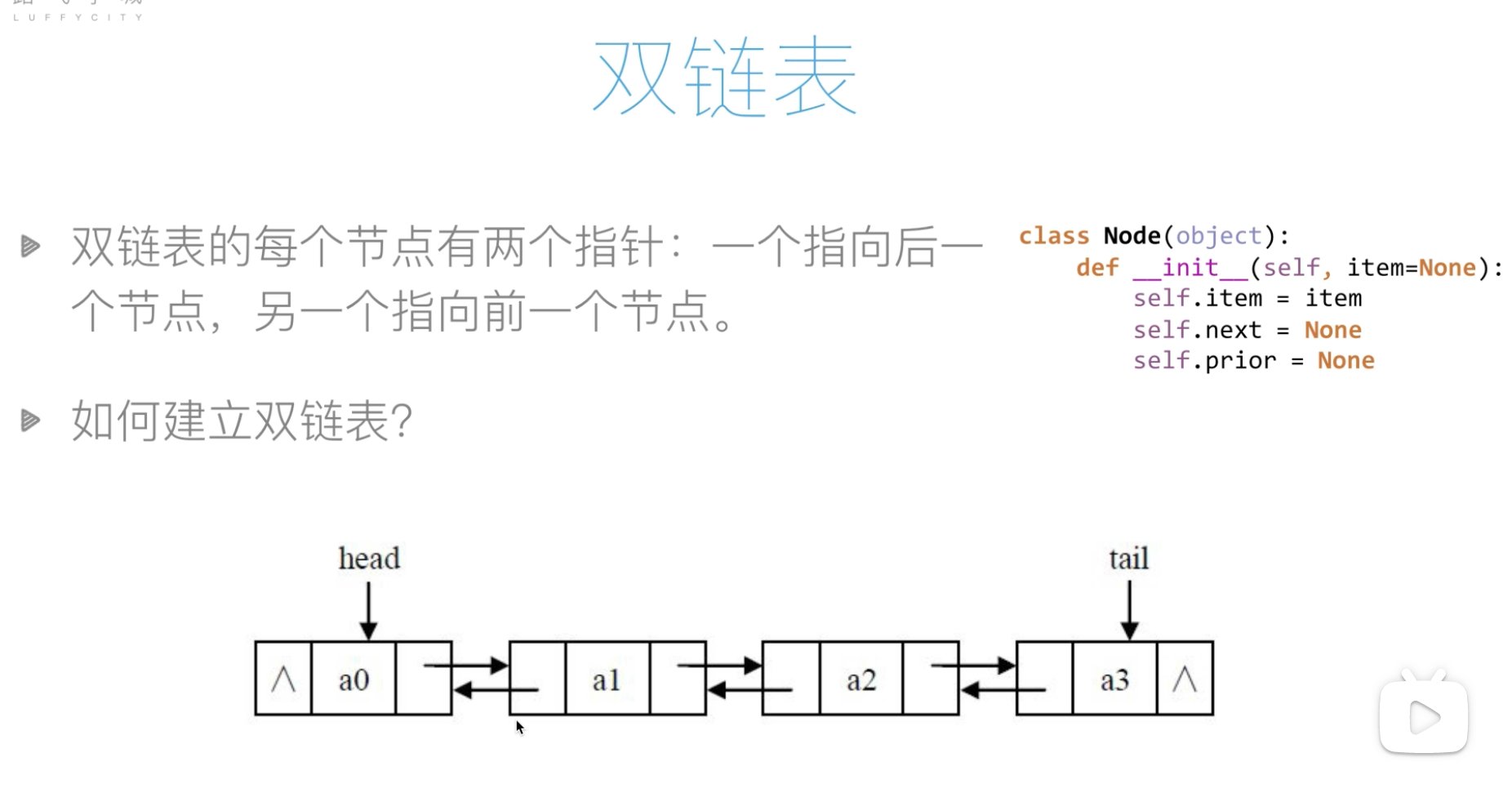
type node struct {
	data       string
	headerNode *node
	tailNode   *node
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}

	a.tailNode = &b
	b.headerNode = &a
	b.tailNode = &c
	c.headerNode = &b

	fmt.Println(b.headerNode.data) //a
}

遍历双链表：

type node struct {
	data       string
	headerNode *node
	tailNode   *node
}

//遍历双链表
func freNode(t *node) {
	fmt.Println(t.data)
	if t.tailNode != nil {
		freNode(t.tailNode)
	}
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}

	a.tailNode = &b
	b.headerNode = &a
	b.tailNode = &c
	c.headerNode = &b

	freNode(&a)
}

//输出
a
b
c

双链表头插法：

//双链表头插发
func headerInto(t, h *node) {
	h.tailNode = t
	t.headerNode = h
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}

	a.tailNode = &b
	b.headerNode = &a
	b.tailNode = &c
	c.headerNode = &b

	d := node{data: "d"}

	//头部插入d节点,在a前面插入d
	headerInto(&a, &d)
	fmt.Println(a.headerNode.data) //d
}

双链表尾插法：

//双链表尾插发
func tailInto(t, h *node) {
	t.tailNode = h
	h.headerNode = t
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}

	a.tailNode = &b
	b.headerNode = &a
	b.tailNode = &c
	c.headerNode = &b

	d := node{data: "d"}

	//尾插入d节点,在c后面面插入d
	tailInto(&c, &d)
	fmt.Println(c.tailNode.data) //d
}

双链表中间插入：

//双链中间插入
func inInto(t, h *node) {
	h.tailNode = t.tailNode
	t.tailNode = h
	h.headerNode = t
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}

	a.tailNode = &b
	b.headerNode = &a
	b.tailNode = &c
	c.headerNode = &b

	d := node{data: "d"}

	//b节点后插入d节点
	inInto(&b, &d)
	fmt.Println(b.tailNode.data) //d
	fmt.Println(b.tailNode.tailNode.data) //c
}

双链表删除节点：

//删除中间节点
func delNode(t *node) {
	t.headerNode.tailNode = t.tailNode
	t.tailNode.headerNode = t.headerNode
}

func TestNode() {
	a := node{data: "a"}
	b := node{data: "b"}
	c := node{data: "c"}

	a.tailNode = &b
	b.headerNode = &a
	b.tailNode = &c
	c.headerNode = &b

	//删除b中间节点
	delNode(&b)

	fmt.Println(a.tailNode.data) //c
}

链表总结

链表：
	1.链表在插入和删除的操作明显比顺序表快
	2.内存分配灵活
 

链表：
1.按元素查找
	O(n)
2.按下标查找
	O(n)
3.在某元素后插入
	O(1)
4.删除某元素
	O(1)

列表元组(顺序表)：
1.按元素查找
	O(n)
2.按下标查找
	O(1)
3.在某元素后插入
	O(n)
4.删除某元素
	O(n)