常规算法

目录

贪心算法

找零问题

代码：

def change(n):
    t = [100, 50, 20, 5, 1]  # 钱的种类
    m = [0 for _ in range(len(t))]

    for index, monery in enumerate(t):
        m[index] = n // monery
        n = n % monery
    print(m)
    return m

if __name__ == '__main__':
    change(999)  # [9, 1, 2, 1, 4]
    change(999)  # [1, 0, 1, 0, 3]

背包问题

背包容量50kg，怎么装东西以达到最大的价值？

def backpack(goods, w):
    m = [0 for _ in range(len(goods))]
    total = 0
    for i, (prize, weight) in enumerate(goods):
        if w > weight:
            m[i] = 1
            total += prize  # 当前拿到的价值
            w -= weight  # 背包剩余重量
        else:
            m[i] = w / weight
            total += m[i] * prize
            w = 0  # 背包装满
            break
    return total, m


if __name__ == '__main__':
    # 3类物品，价值60元钟10kg,价值100元重20kg,价值120元重30kg
    goods = [(60, 10), (100, 20), (120, 30)]
    w = 50  # 背包承受重量
    a = backpack(goods, w)
    print(a)

拼接数字最大问题

代码：

# 例如：32,94,128,1286,6,71
# 拼接最大数字为：94 71 6 32 1286 128
from functools import cmp_to_key


def index(li):
    li = list(map(str,li))
    print(li)
    li.sort(key=cmp_to_key(xy_cmp))
    print(li)
    return ''.join(li)


def xy_cmp(x,y):
    if x+y < y+x:
        return 1
    elif x+y > y+x:
        return -1
    else:
        return 0


if __name__ == '__main__':
    li = [32, 94, 128, 1286, 6, 71]
    print(index(li))

活动选择问题

代码：

active = [(1, 4), (0, 6), (5, 9), (8, 12), (2, 14), (12, 16), (3, 5), (6, 10), (8, 11), (5, 7), (3, 9)]

# 保证活动是按结束时间排好序的
active.sort(key=lambda x: x[1])


def activtty_selection(active):
    res = [active[0]]  # 活动列表
    for i in range(1, len(active)):
        start_time = active[i][0]  # 活动开始时间
        if res[-1][1] <= start_time:  # 当前活动的开始时间小于等于列表中最后一个活动的结束时间
            res.append(active[i])
    print(res)
    return res


if __name__ == '__main__':
    activtty_selection(active)

动态规划

钢条切割

代码：时间复杂度O(n方)

import time


def cal_time(func):
    def wrapper(*args,**kwargs):
        t1 = time.time()
        result = func(*args,**kwargs)
        t2 = time.time()
        print("耗时：", t2-t1)
        return result
    return wrapper

@cal_time
def cut_rod_dp(p, n):
    r = [0]
    for i in range(1, n + 1):
        res = 0
        for j in range(1, i + 1):
            res = max(res, p[j] + r[i - j])
        r.append(res)
    print(r[n])
    print(r)
    print(len(r))
    return r[n]


if __name__ == '__main__':
    p = [0, 1, 5, 8, 9, 10, 17, 18, 20, 21, 23, 24, 26, 27, 27, 28, 30, 33, 36, 39, 40]
    n = 20  # 钢条长度
    cut_rod_dp(p, n)

最长公共子序列

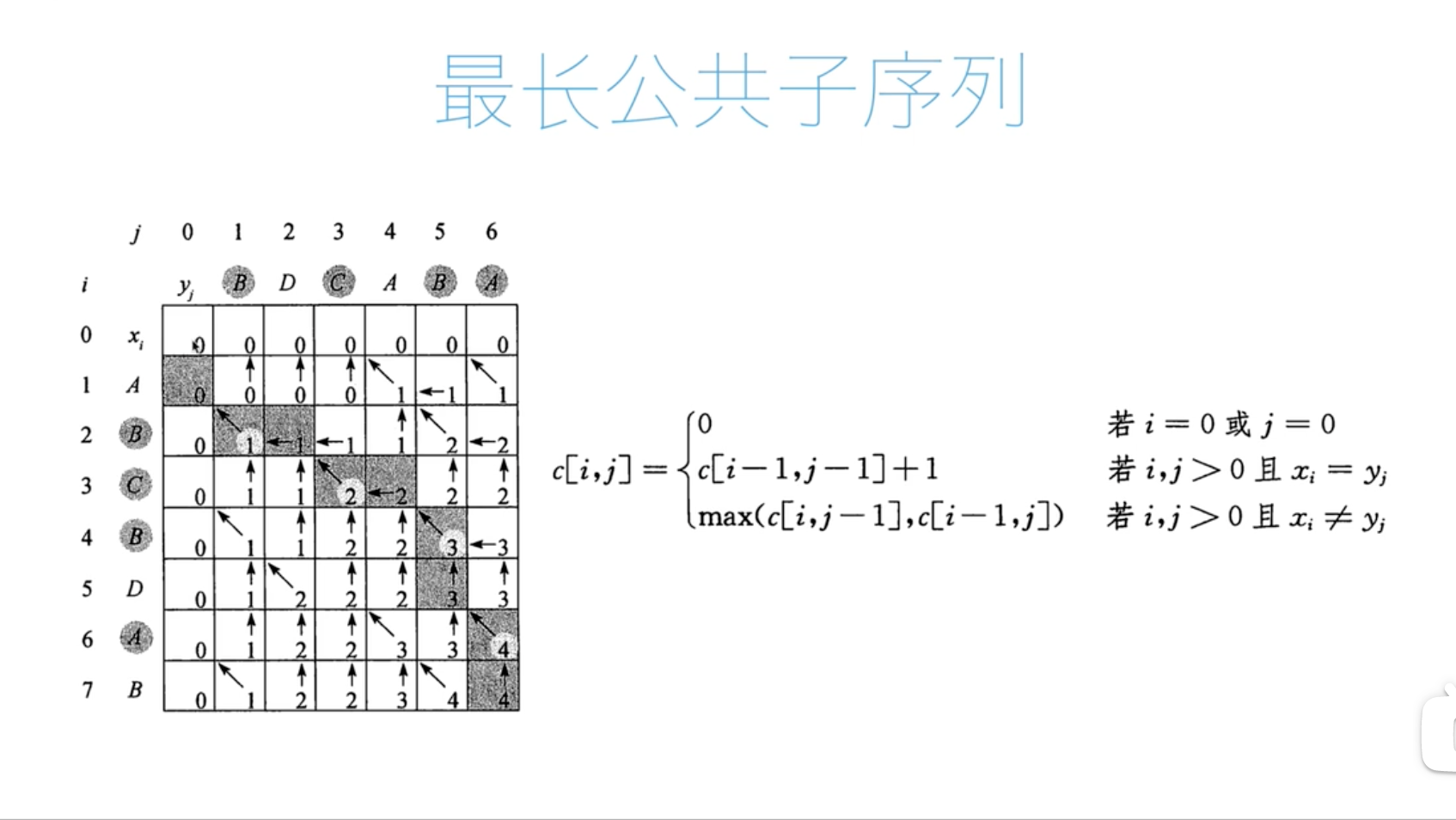
代码：

# 最长公共子序列长度算法
def lcs_length(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j 位置上的自负匹配的时候，来自左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
            else:
                c[i][j] = max(c[i - 1][j], c[i][j - 1])
    for _ in c:
        print(_)
    return c[m][n]

# 最长公共子序列方向算法
def lcs(x, y):
    m = len(x)
    n = len(y)
    c = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    b = [[0 for _ in range(n + 1)] for _ in range(m + 1)]
    for i in range(1, m + 1):
        for j in range(1, n + 1):
            if x[i - 1] == y[j - 1]:  # i j 位置上的自负匹配的时候，来自左上方+1
                c[i][j] = c[i - 1][j - 1] + 1
                b[i][j] = 1
            elif c[i - 1][j] > c[i][j - 1]:  # 来自于上方
                c[i][j] = c[i - 1][j]
                b[i][j] = 2
            else:
                c[i][j] = c[i][j - 1]
                b[i][j] = 3
    return c[n][n], b


# 最长公共子序列回溯算法
def lcs_trackback(x, y):
    c, b = lcs(x, y)
    i = len(x)
    j = len(y)
    res = []
    while i > 0 and j > 0:
        if b[i][j] == 1:  # 来自左上方=》匹配
            res.append(x[i - 1])
            i -= 1
            j -= 1
        elif b[i][j] == 2:  # 来自上方=》不匹配
            i -= 1
        else:  # 来自作坊=》不匹配
            j -= 1
    return "".join(reversed(res))


if __name__ == '__main__':
    x = "ABCBDAB"
    y = "BDCABA"
    res = lcs_trackback(x, y)
    print(res)

欧几里得算法

动态演示：

https://www.bilibili.com/video/BV1Qv411t7sa?p=95&spm_id_from=pageDriver

代码：

# 循环写法1
def gcd2(x, y):
    while True:
        a = x % y
        if a != 0:
            x = y
            y = a
        else:
            return y


# 循环写法2
def gcd3(x, y):
    while y > 0:
        a = x % y
        x = y
        y = a
    return x


# 递归写法
def gcd(x, y):
    if y == 0:
        return x
    else:
        return gcd(y, x % y)


if __name__ == '__main__':
    res = gcd2(105, 252)
    # res = gcd2(252, 105)
    print(res)
    # res = gcd2(100,21)
    # print(res)

RSA算法过程

posted @ 2021-02-22 15:19  Jeff的技术栈  阅读(117)  评论(0)  编辑  收藏  举报
回顶部