数据结构
目录
时间复杂度

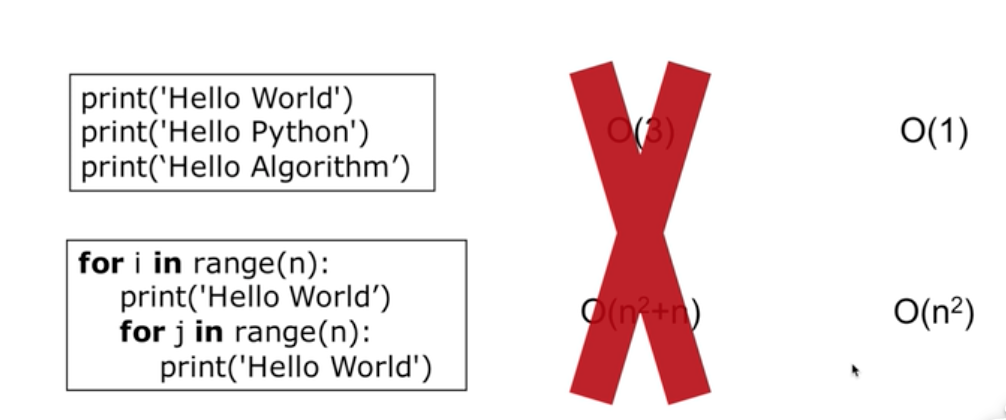
循环减半

快速判断时间复杂度

小结

空间复杂度

递归--涵洛塔问题
视频讲解
https://www.bilibili.com/video/BV1Qv411t7sa?p=6

解决思路
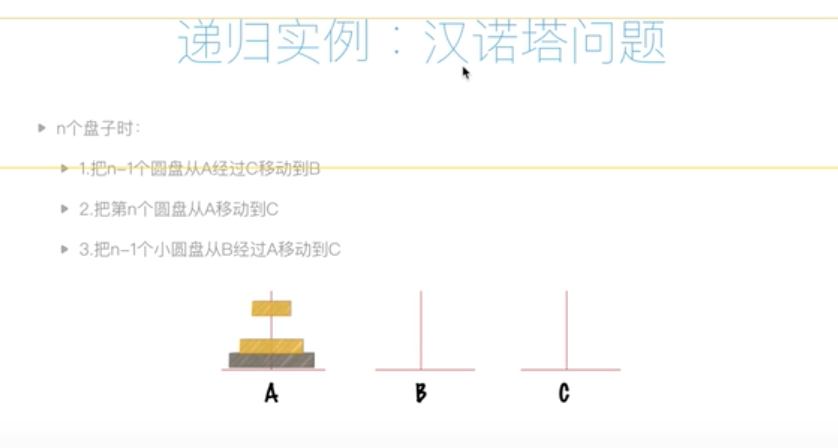
解决代码
num = 0
def hanoi(n, a, b, c):
"""
递归贝诺塔问题,abc三个棍子,目的:全部移动到另一更棍子
:param n: 盘子数
:param a: 棍子a
:param b: 棍子b
:param c: 棍子c
:return:
"""
global num
if n > 0:
hanoi(n - 1, a, c, b) # n-1个盘子从a经过c移动到b
# print(f'{n - 1}个盘子从a经过c移动到b')
num += 1
hanoi(n - 1, b, a, c)
if __name__ == '__main__':
hanoi(3, "A", "B", "C")
print(num)
顺序查找
时间复杂度:O(n)
def search_test(li, num):
for i in li:
if i == num:
return li.index(num)
return None
if __name__ == '__main__':
li = [1, 2, 3, 4, 5, 111, 222, 333, 8, 11, 22, 33, 9]
print(search_test(li, 100))
二分法查找
时间复杂度:O(logn) 循环减半
前提条件:列表必须有序
def bin_search(li, num, left, right):
if left < right:
mid = (left + right) // 2
if li[mid] == num:
return mid
elif li[mid] > num:
return bin_search(li, num, left, mid-1)
elif li[mid] < num:
return bin_search(li, num, mid+1, right)
else:
return
if __name__ == '__main__':
li = [1, 2, 3, 4, 5, 6, 7]
num = 6
left = 0
right = len(li)
print(bin_search(li, num, left, right))
常见排序算法

树与二叉树
树
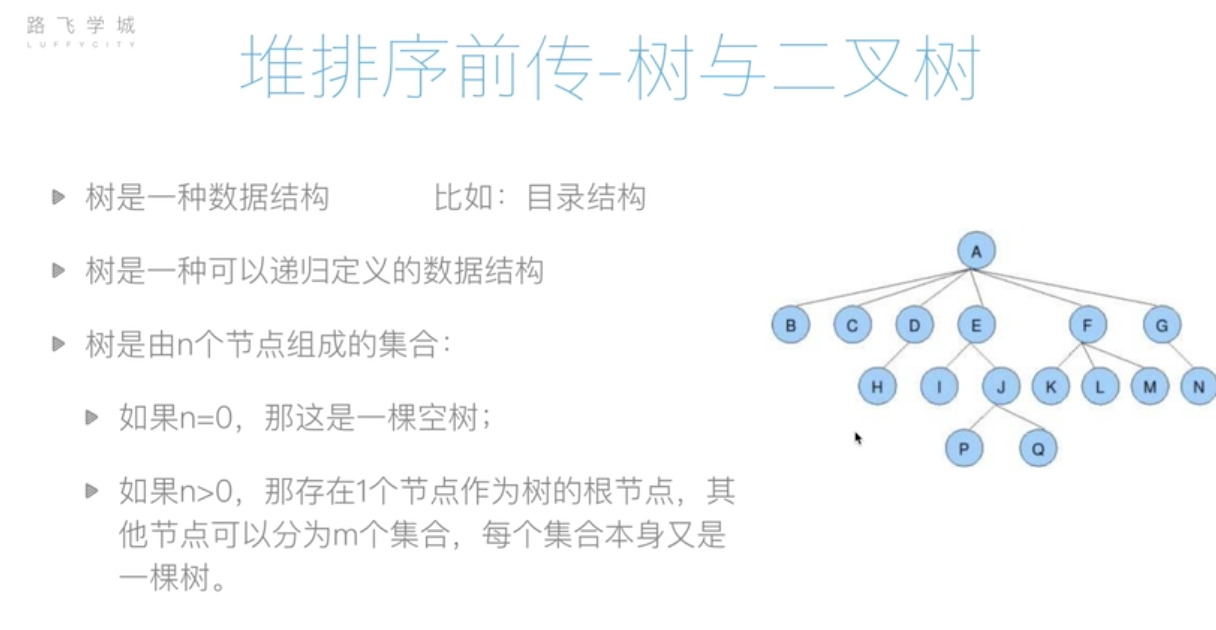
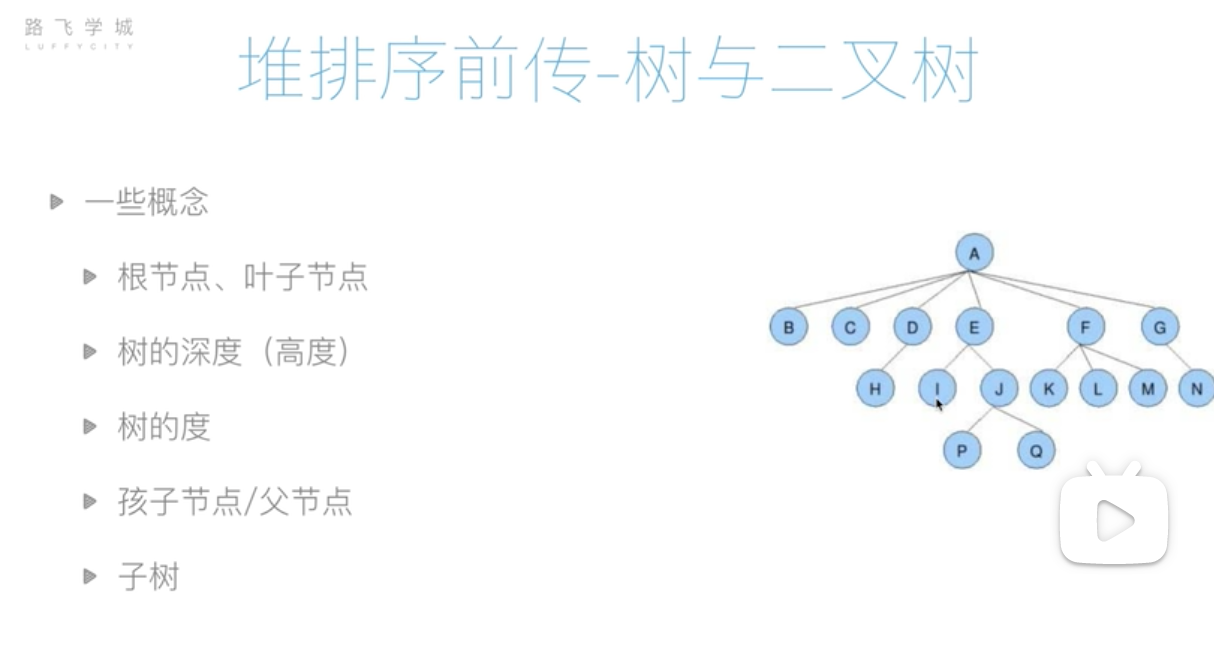
根节点:最开始的位置。A
叶子结点:不能分叉的结点。 BCHKLMNPQ
树的深度:最深有几层。4
树的度:整个树里最大节点的度,节点的分叉树量。本图最大节点A的度为6
节点的度:节点的分叉树。F的度为3,E的度为2
父节点:H的父节点为D节点
孩子节点:D的孩子节点为H节点
子树:整个树中的一部分,比如:E节点子树就代表EIJPQ
二叉树

代码演示
class BirTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None # 左孩子
self.rchild = None # 右孩子
a = BirTreeNode('A')
b = BirTreeNode('B')
c = BirTreeNode('C')
d = BirTreeNode('D')
e = BirTreeNode('E')
f = BirTreeNode('F')
g = BirTreeNode('G')
h = BirTreeNode('H')
i = BirTreeNode('I')
a.rchild = c
a.lchild = b
b.rchild = e
b.lchild = d
d.rchild = g
d.lchild = f
g.rchild = i
g.rchild = h
root = a # 亘节点
print(a.lchild.lchild.data) # a的左孩子的左孩子
满二叉树,完全二叉树
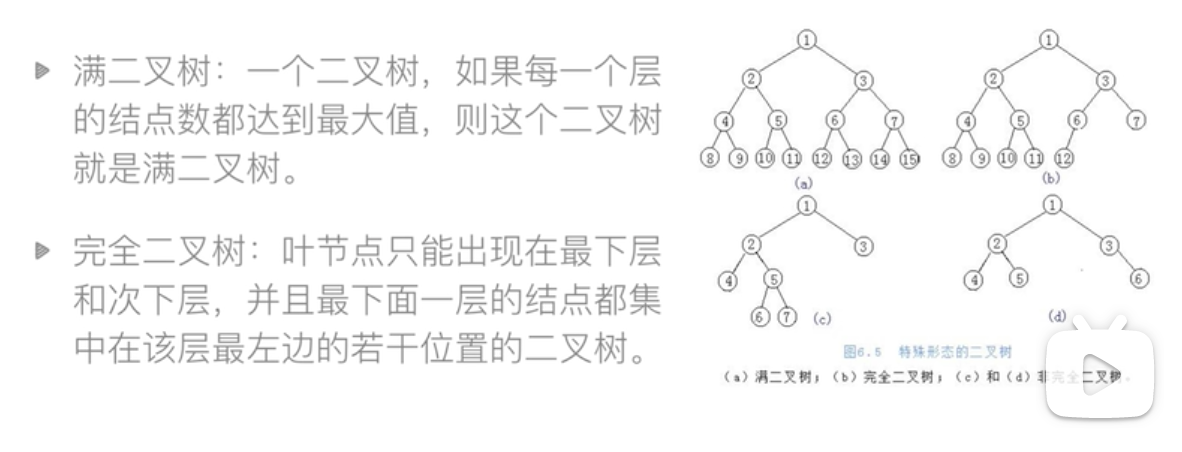
遍历二叉树

from collections import deque
class BirTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None # 左孩子
self.rchild = None # 右孩子
a = BirTreeNode('A')
b = BirTreeNode('B')
c = BirTreeNode('C')
d = BirTreeNode('D')
e = BirTreeNode('E')
f = BirTreeNode('F')
g = BirTreeNode('G')
h = BirTreeNode('H')
i = BirTreeNode('I')
a.rchild = c
a.lchild = b
b.rchild = e
b.lchild = d
d.rchild = g
d.lchild = f
g.rchild = i
g.lchild = h
root = a
# ABDFGHIEC
# 前序遍历
def pre_order(root):
if root:
print(root.data, end='') # 访问自己
pre_order(root.lchild) # 递归左子树
pre_order(root.rchild) # 递归右子树
# FDHGIBEAC
# 中序遍历
def in_order(root):
if root:
in_order(root.lchild) # 递归左子树
print(root.data, end='') # 访问自己
in_order(root.rchild) # 递归右子树
# FHIGDEBCA
# 后序遍历
def post_order(root):
if root:
post_order(root.lchild) # 递归左子树
post_order(root.rchild) # 递归右子树
print(root.data, end='') # 访问自己
# ABCDEFGHI
# 层次遍历
def level_order(root):
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
print(node.data,end='')
if node.lchild:
queue.append(node.lchild)
if node.rchild:
queue.append(node.rchild)
if __name__ == '__main__':
# pre_order(root)
# in_order(root)
# post_order(root)
level_order(root)
二叉搜索树

二叉搜索树插入/查询/遍历
class BirTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None # 左孩子
self.rchild = None # 右孩子
self.parent = None # 父节点
class BST:
def __init__(self, li=None):
self.root = None
if li:
for val in li:
self.insert_no_rec(val)
# 插入递归方法
def insert(self, node, val):
if not node:
node = BirTreeNode(val)
elif val < node.data:
node.lchild = self.insert(node.lchild, val)
node.lchild.parent = node
elif val > node.data:
node.rchild = self.insert(node.rchild, val)
node.rchild.parent = node
return node
# 插入非递归方法
def insert_no_rec(self, val):
p = self.root
if not p: # 空树
self.root = BirTreeNode(val)
return
while True:
if val < p.data:
if p.lchild:
p = p.lchild
else: # 左孩子不存在
p.lchild = BirTreeNode(val)
p.lchild.parent = p
elif val > p.data:
if p.rchild:
p = p.rchild
else:
p.rchild = BirTreeNode(val)
p.rchild.parent = p
return
else:
return
# 查询递归方法
def query(self, node, val):
if not node:
return None
if node.data < val:
return self.query(node.rchild, val)
elif node.data > val:
return self.query(node.lchild, val)
else:
return node
# 查询非递归方法
def query_no_rec(self,val):
p = self.root
while p:
if p.data < val:
p = p.rchild
elif p.data > val:
p = p.lchild
else:
return p
return None
# 前序遍历
def pre_order(self, root):
if root:
print(root.data, end='') # 访问自己
self.pre_order(root.lchild) # 递归左子树
self.pre_order(root.rchild) # 递归右子树
# 中序遍历
def in_order(self, root):
if root:
self.in_order(root.lchild) # 递归左子树
print(root.data, end='') # 访问自己
self.in_order(root.rchild) # 递归右子树
# 后序遍历
def post_order(self, root):
if root:
self.post_order(root.lchild) # 递归左子树
self.post_order(root.rchild) # 递归右子树
print(root.data, end='') # 访问自己
if __name__ == '__main__':
tree = BST([4, 5, 6, 1, 2, 3, 7, 9, 8])
print(tree.query_no_rec(3).data) # 非递归查询
print(tree.query(tree.root, 3).data) # 递归查询
# 排序
tree.pre_order(tree.root) # 412356798
print('')
tree.in_order(tree.root) # 123456789
print('')
tree.post_order(tree.root) # 321897654
二叉树搜索效率

平均:o(lgn) 循环减半
最坏的情况,偏斜变成链表:o(n)
解决方案:
随机插入
AVL树
AVL树
https://www.bilibili.com/video/BV1Qv411t7sa?p=75&spm_id_from=pageDriver
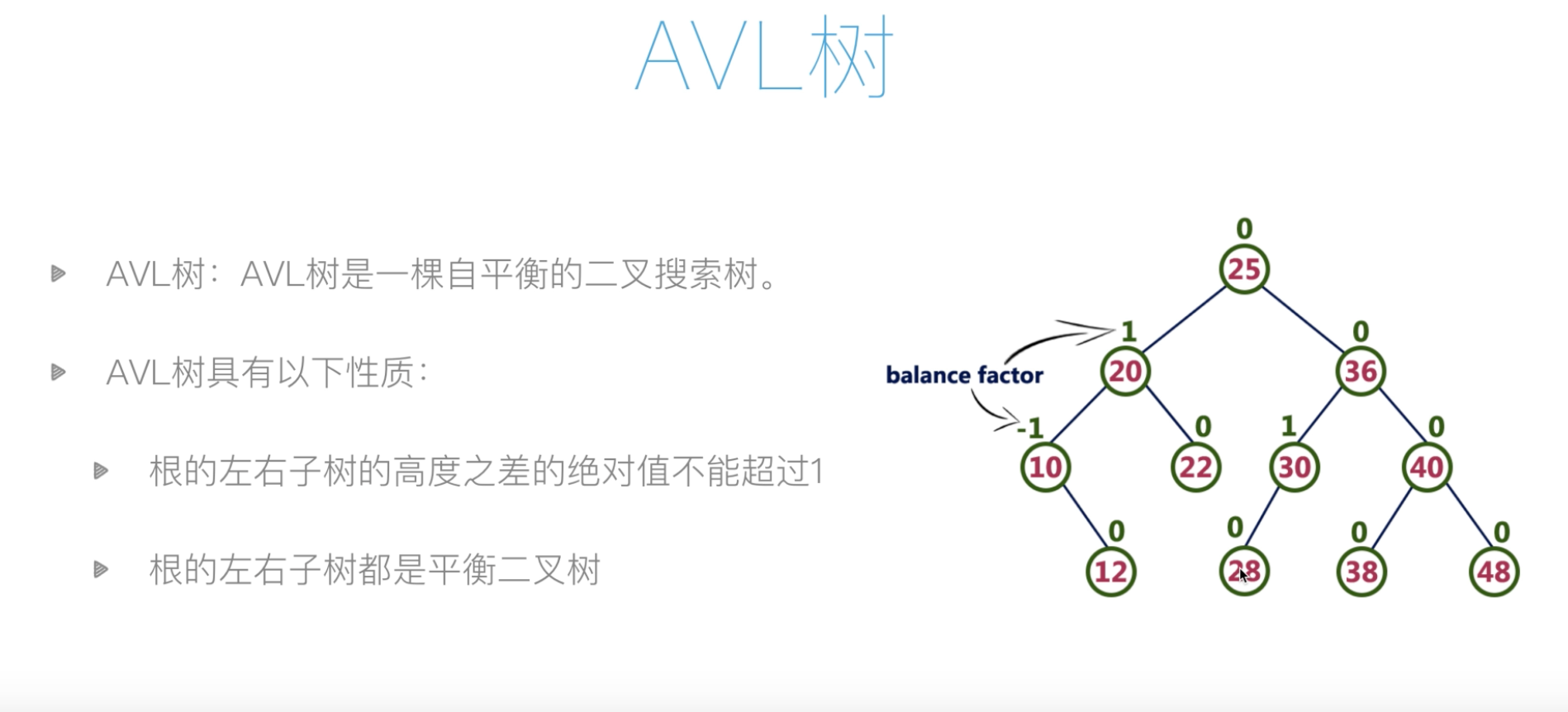

AVL插入-左旋
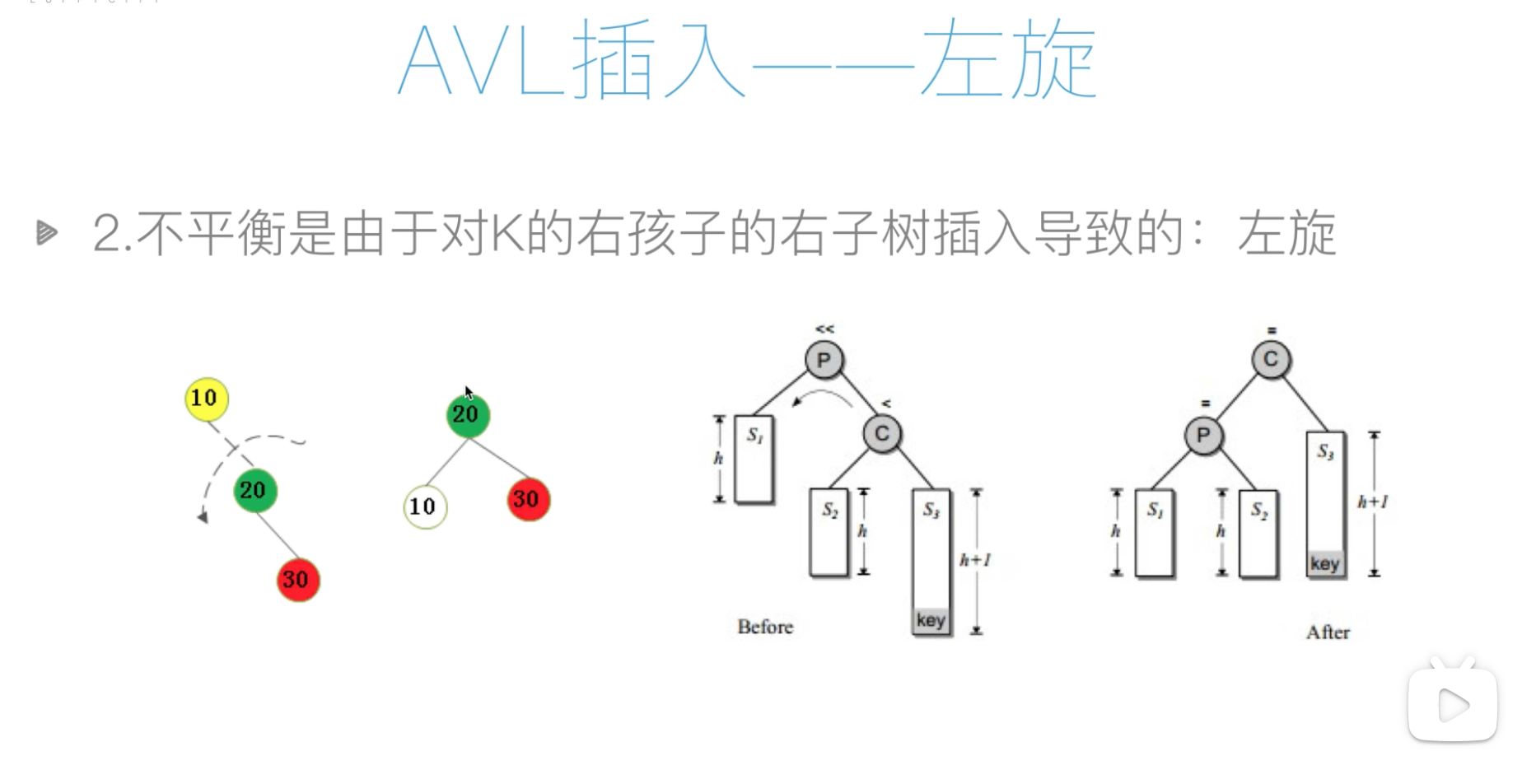
AVL插入-右旋
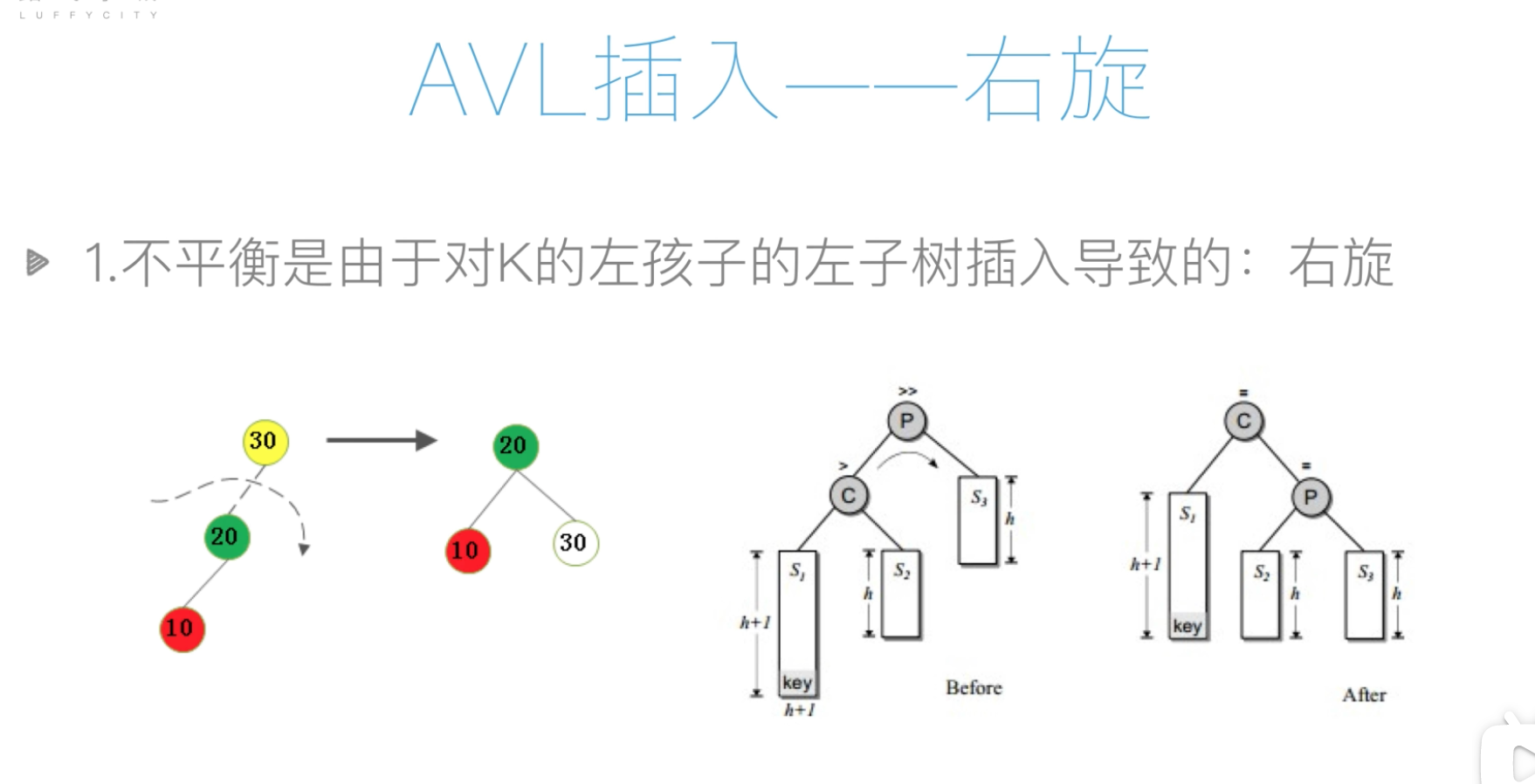
AVL插入-右旋左旋
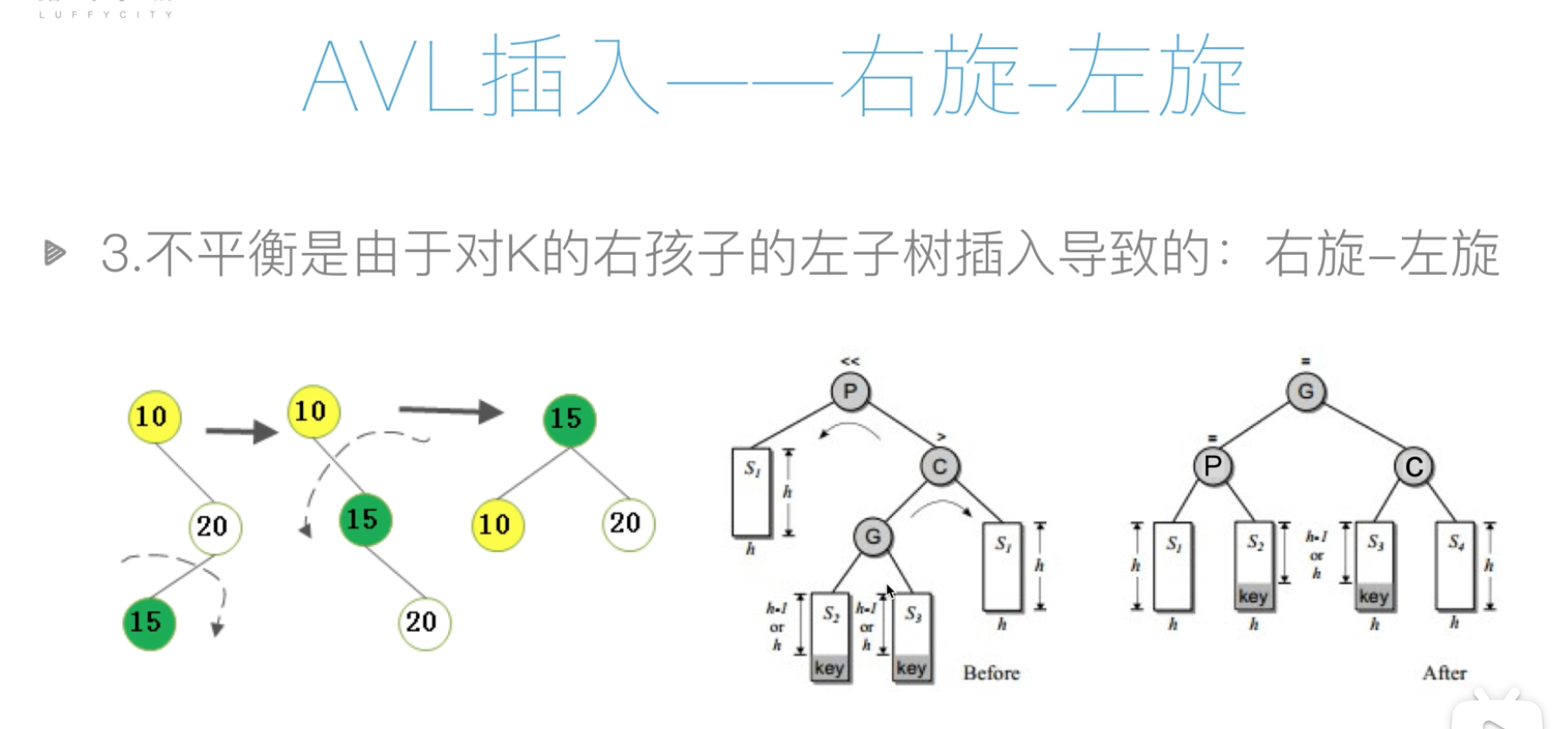
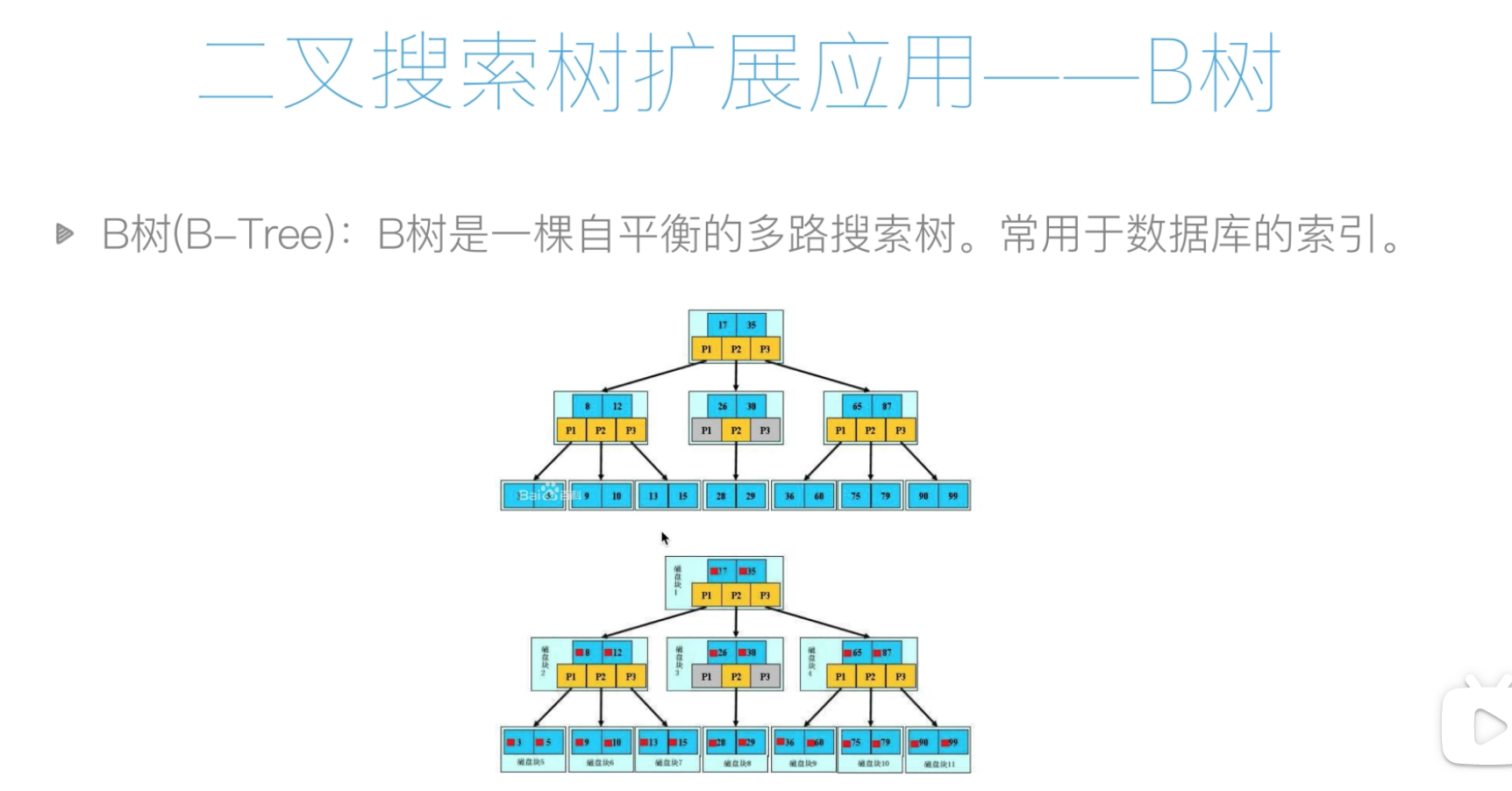
B树
B树特点:
1.所有健值分布在整棵树中
2.搜索有可能在非叶子结点结束,效率接近二分查找
3.每个节点最多拥有m(无穷)颗子树
4.根结点最少有两颗子树
5.分支节点至少有m/2颗子树(除根结点和叶子结点外都是分支节点)
缺点:
1.每个磁盘空间有4k,如果数据data太大,那么导致树的深度加深,查询变慢
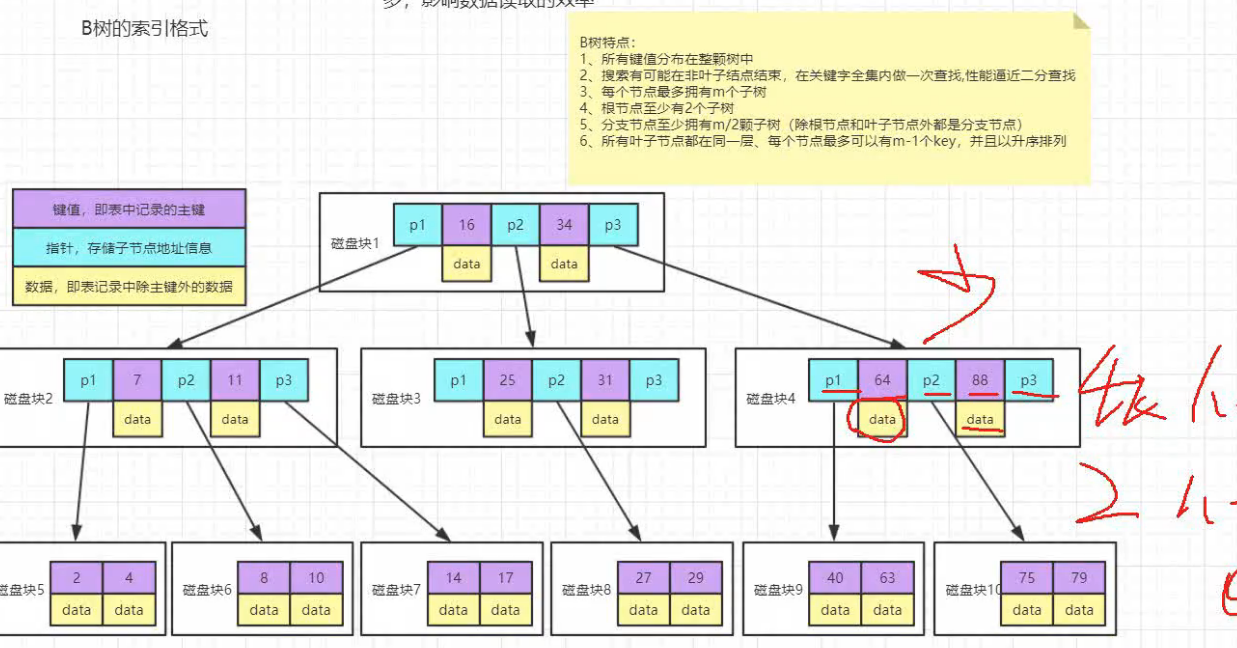
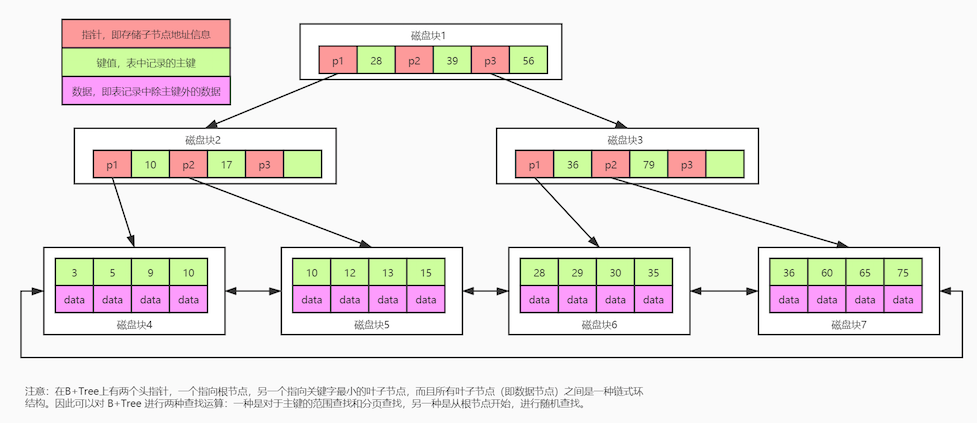
B+树
特点:B+树是在B树基础之上的优化
1.B+树每个节点包含更多的节点,原因1:降低树的高度,原因2:将数据的范围变为多个区间,区间越多数据检索越快
2.非叶子结点存储key,叶子结点存储key和数据
3.叶子结点俩俩指针相互连接(符合磁盘的预读特性),顺讯查询时性能更高
Innodb每次预读16k,4k的整数倍
mysql索引数据结构:
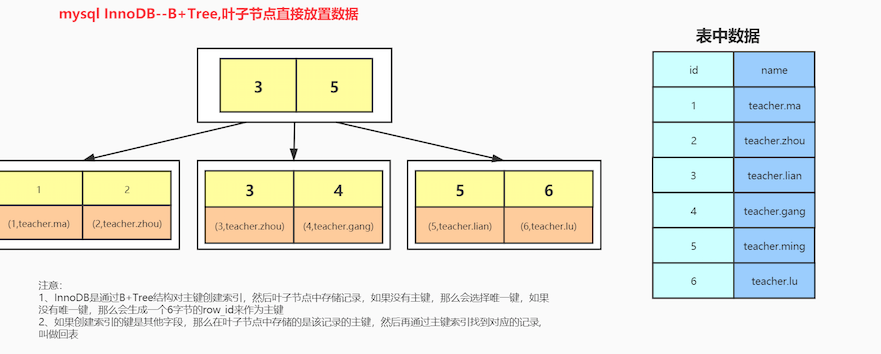
mysql InnoDB B+树
注意:
1.InnoDB是通过对B+树结构对主键创建索引,然后叶子结点中储存记录,如果没有主键,那么选择唯一健,如过没有唯一健,那么会生成6字节的row_id作为主键
2.如果创建索引的健是其他字段,那么在叶子节点中储存的是该记录的主键,然后再通过主键索引找到对应的记录,叫做回表
创建的索引是主键:叶子结点存储数据
创建的索引不是主键:叶子结点存储主键值,再通过主键值找到对应的数据。走了两遍B+树
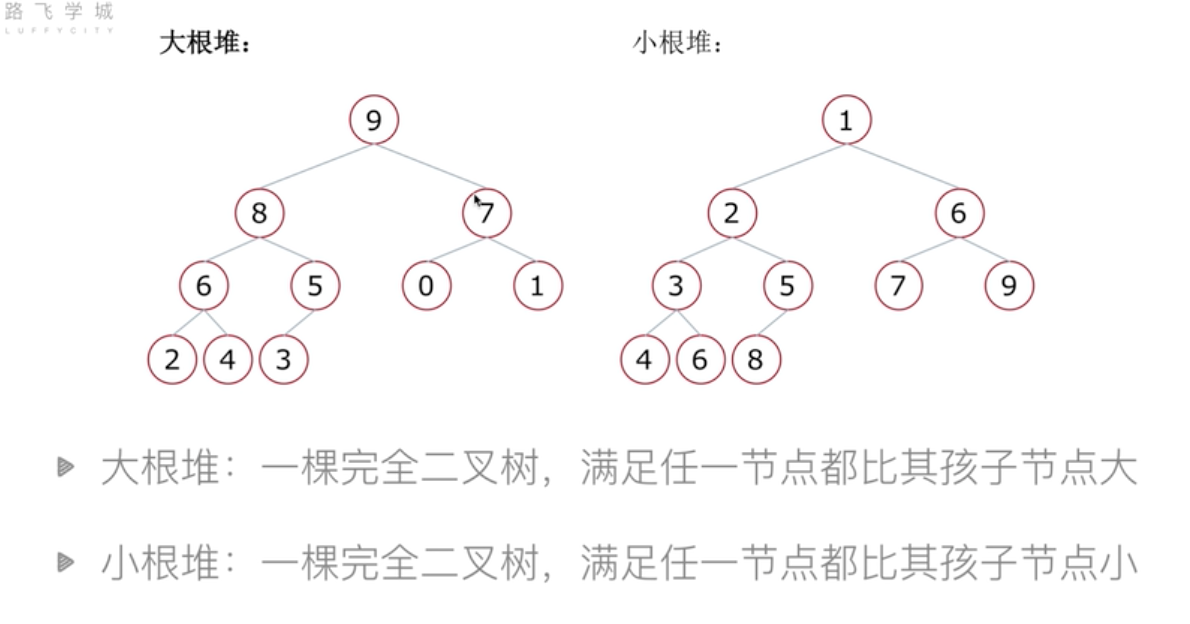
堆
https://www.bilibili.com/medialist/play/ml1147652374/BV1Qv411t7sa

栈--迷宫问题

maze = [
[1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
[0, 0, 0, 1, 1, 0, 0, 0, 1, 1],
[1, 1, 0, 0, 0, 0, 1, 0, 1, 1],
[1, 1, 0, 0, 1, 0, 1, 1, 1, 1],
[1, 1, 1, 0, 1, 0, 1, 1, 1, 1],
[1, 1, 1, 0, 1, 1, 1, 1, 1, 1],
[1, 0, 0, 0, 0, 1, 1, 1, 1, 1],
[1, 0, 1, 1, 0, 0, 0, 0, 0, 1],
[1, 1, 1, 1, 1, 1, 1, 1, 0, 1],
]
dirs = [
lambda x, y: (x + 1, y), # 右
lambda x, y: (x, y + 1), # 下
lambda x, y: (x - 1, y), # 左
lambda x, y: (x, y - 1), # 上
]
def maze_path(x1, y1, x2, y2):
"""
:param x1: 起点坐标
:param y1: 起点坐标
:param x2: 终点坐标
:param y2: 终点坐标
:return:
"""
stack = []
stack.append((x1, y1))
# 栈为空,则证明没有路通向终点
while (len(stack) > 0):
curNode = stack[-1] # 当前所在节点
# 如果走到终点
if curNode[0] == x2 and curNode[1] == y2:
for p in stack:
print(p)
return
for dir in dirs:
nextNode = dir(curNode[0], curNode[1])
# 如果下一个节点能走
if maze[nextNode[0]][nextNode[1]] == 0:
stack.append(nextNode)
maze[nextNode[0]][nextNode[1]] = 2 # 表示已经走过
break
else:
maze[nextNode[0]][nextNode[1]] = 2
stack.pop()
else:
print('无路可走')
return False
if __name__ == '__main__':
maze_path(0, 1, 7, 8)
链表-头插法/尾插法

# 链表
class Node:
def __init__(self, item):
self.item = item
self.next = None
# 1.头插法
def create_linklist(li):
head = Node(li[0]) # 链表的头
for data in li[1:]:
node = Node(data) # 值
node.next = head # 下一位的值
head = node # 重新赋值链表头
return head
# 尾插法
def create_linklist_tail(li):
head = Node(li[0])
tail = head
for data in li[1:]:
node = Node(data)
tail.next = node
tail = node
return head
# 链表的遍历
def print_linklist(head):
while head:
print(head.item)
head = head.next
if __name__ == '__main__':
# 头插
li = [1,2,3]
head = create_linklist(li)
print(head.next.next.item)
print_linklist(head) # 遍历
# 尾插
li = [1,2,3]
head = create_linklist_tail(li)
print(head.next.next.item)
pass
单链表的节点插入/删除
单链表:只能从前往后找
双链表:前后都能找
插入
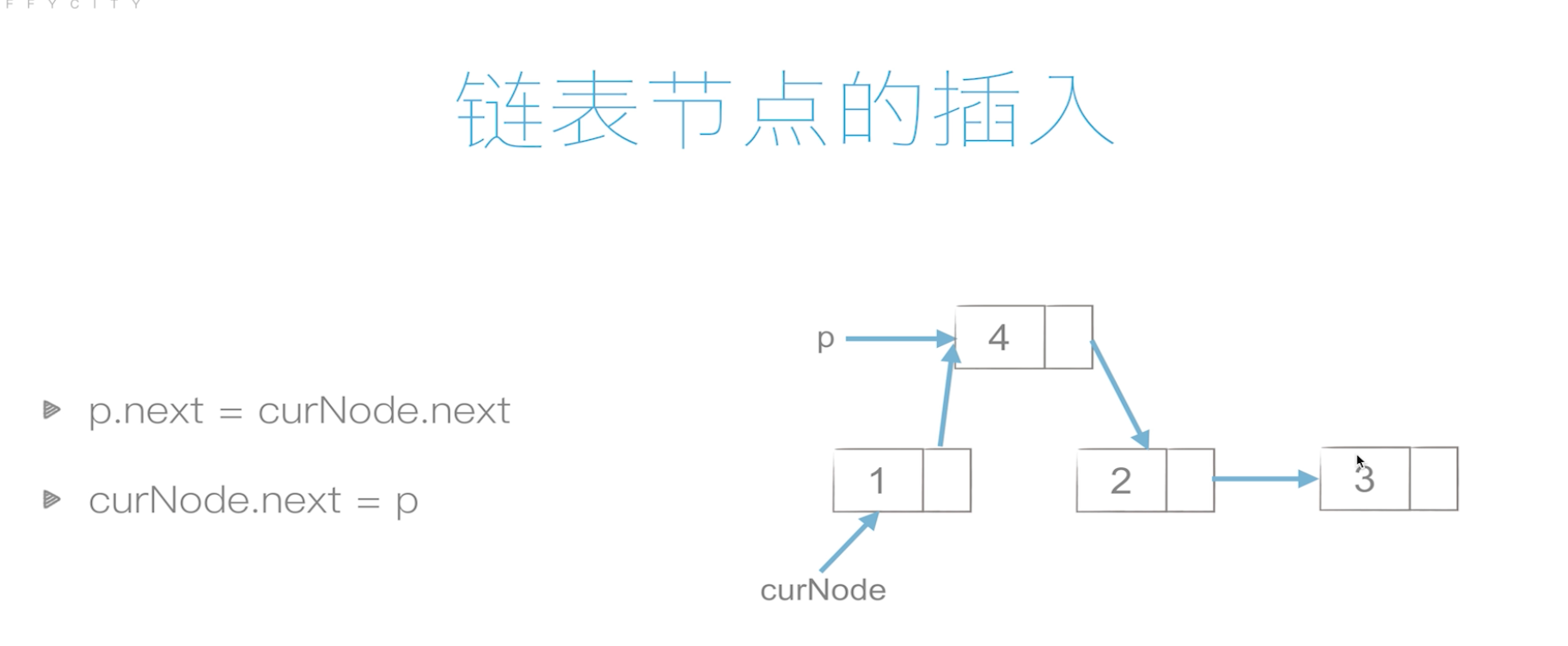
删除
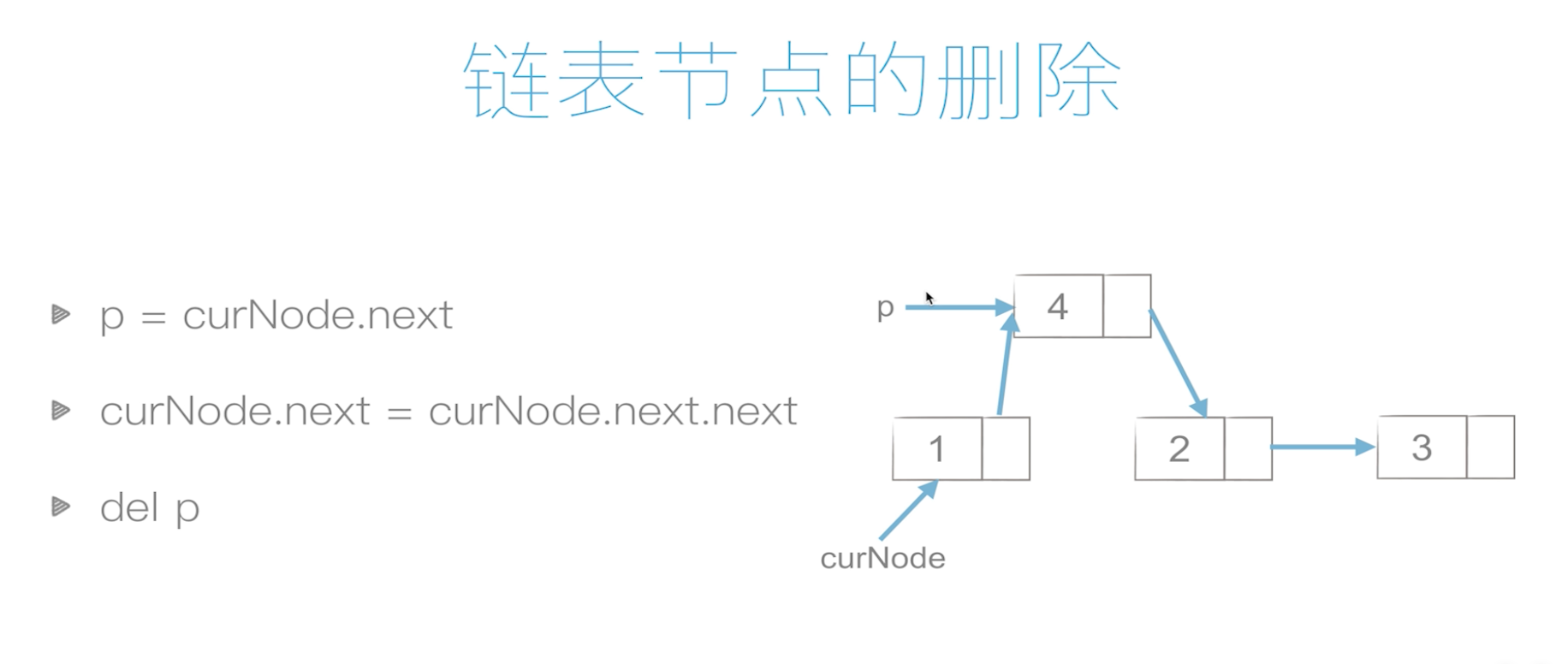
# 链表
class Node:
def __init__(self, item):
self.item = item
self.next = None
# 1.头插法
def create_linklist(li):
head = Node(li[0]) # 链表的头
for data in li[1:]:
node = Node(data) # 值
node.next = head # 下一位的值
head = node # 重新赋值链表头
return head
# 尾插法
def create_linklist_tail(li):
head = Node(li[0])
tail = head
for data in li[1:]:
node = Node(data)
tail.next = node
tail = node
return head
# 链表的遍历
def print_linklist(head):
while head:
print(head.item)
head = head.next
# 链表插入,时间复杂度O(1)
def index_linklist(head):
p = Node(4) # 把p插入到第一个head后面
p.next = head.next
head.next = p
return head
# 链表删除,时间复杂度O(1)
def del_linklist(head):
p = head.next # 删除2元素
head.next = p.next # 或者head.next = head.next.next
return head
if __name__ == '__main__':
# 头插
li = [1, 2, 3]
head = create_linklist(li)
head = del_linklist(head) # 删除
print_linklist(head) # 遍历
# head = index_linklist(head) # 插入
# print_linklist(head) # 遍历
双链表
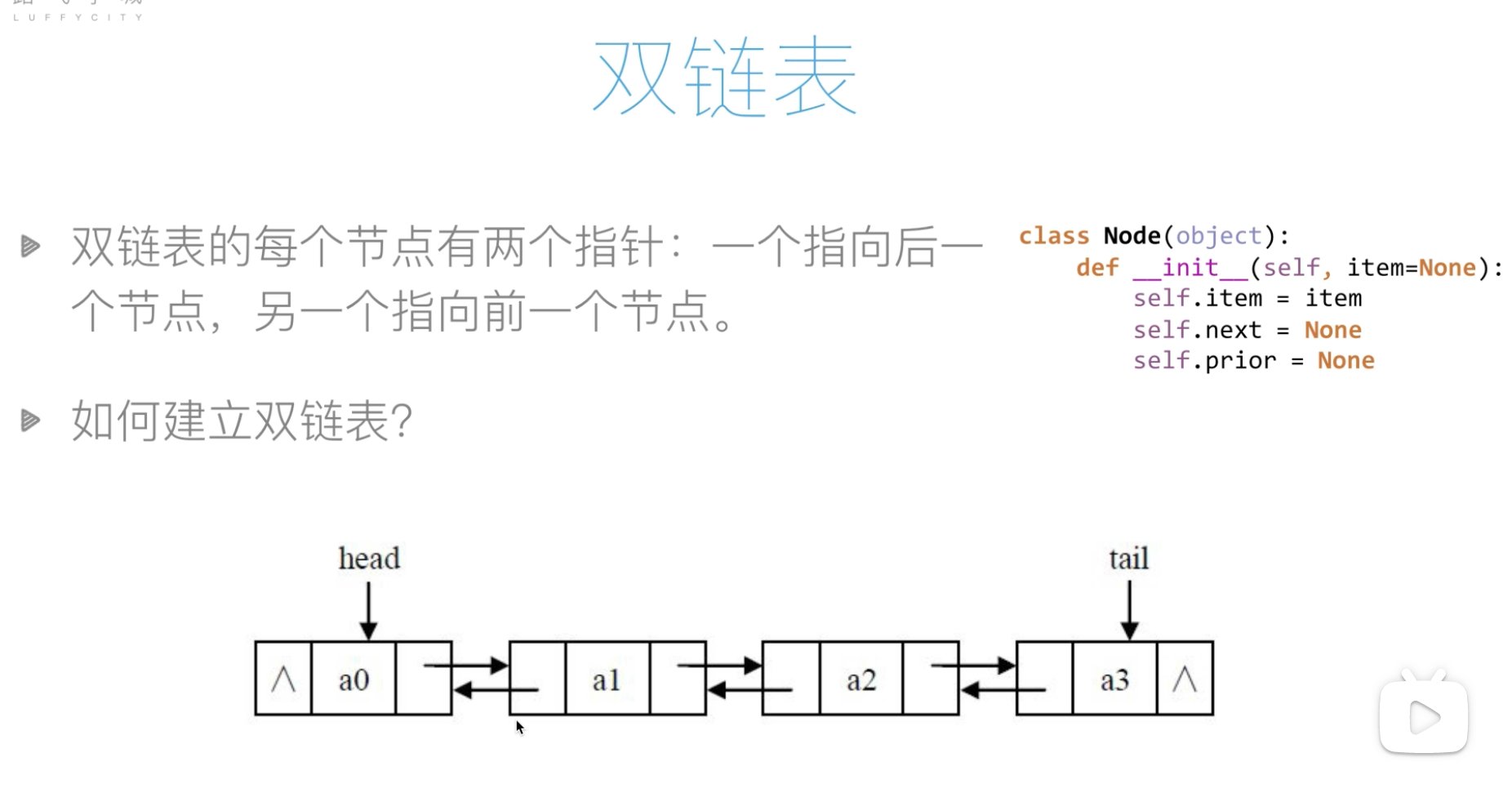
创建
class Node():
def __init__(self, item):
self.item = item
self.next = None
self.prior = None
if __name__ == '__main__':
a = Node(1)
b = Node(2)
c = Node(3)
a.next = b
b.next = c
b.prior = a
c.prior = b
print(a.next.next.prior.item)
双链表头插/尾插法/删除/插入
class Node():
def __init__(self, item):
self.item = item
self.next = None # 下
self.prior = None # 上
# 1.尾插法
def create_linklist_tail(li):
head = Node(li[0]) # 双链表到第一个值,默认为头
res = head # 双链表的头
for data in li[1:]:
node = Node(data) # 插入的值
node.prior = head # 即将插入值的上标=上一个值
head.next = node # 上一个值的下标=插入值
head = node # 重新指向
return res
# 2.头插法
def create_linklist(li):
head = Node(li[0]) # 双链表到第一个值,默认为头
for data in li[1:]:
node = Node(data)
node.next = head
head.prior = node
head = node
return head
# 3.双链表的插入
def index_linklist(head):
p = Node(4) # 把p插入到第一个head后面
p.prior = head
p.next = head.next
head.next = p
head.next.prior = p
return head
# 4.双链表的删除
def del_linklist(head):
p = head.next
head.next = p.next
p.next.prior = head
del p
return head
# 链表的遍历
def print_linklist(head):
while head:
print(head.item)
head = head.next
if __name__ == '__main__':
# 头插法
# li = [1, 2, 3]
# head = create_linklist(li)
# # print(head.next.next.prior.item)
# print_linklist(head)
# 尾插法
li = [1, 2, 3]
head = create_linklist_tail(li)
# head = index_linklist(head) # 插入
head = del_linklist(head) # 删除
# print(head.next.next.prior.item)
print_linklist(head)
链表总结
链表:
1.链表在插入和删除的操作明显比顺序表快
2.内存分配灵活
链表:
1.按元素查找
O(n)
2.按下标查找
O(n)
3.在某元素后插入
O(1)
4.删除某元素
O(1)
列表元组(顺序表):
1.按元素查找
O(n)
2.按下标查找
O(1)
3.在某元素后插入
O(n)
4.删除某元素
O(n)
哈西表

哈西冲突
哈西冲突:哈西函数h(k)返回的key相同,导致两个同样key指向不同的值
解决哈西冲突
开放寻址法

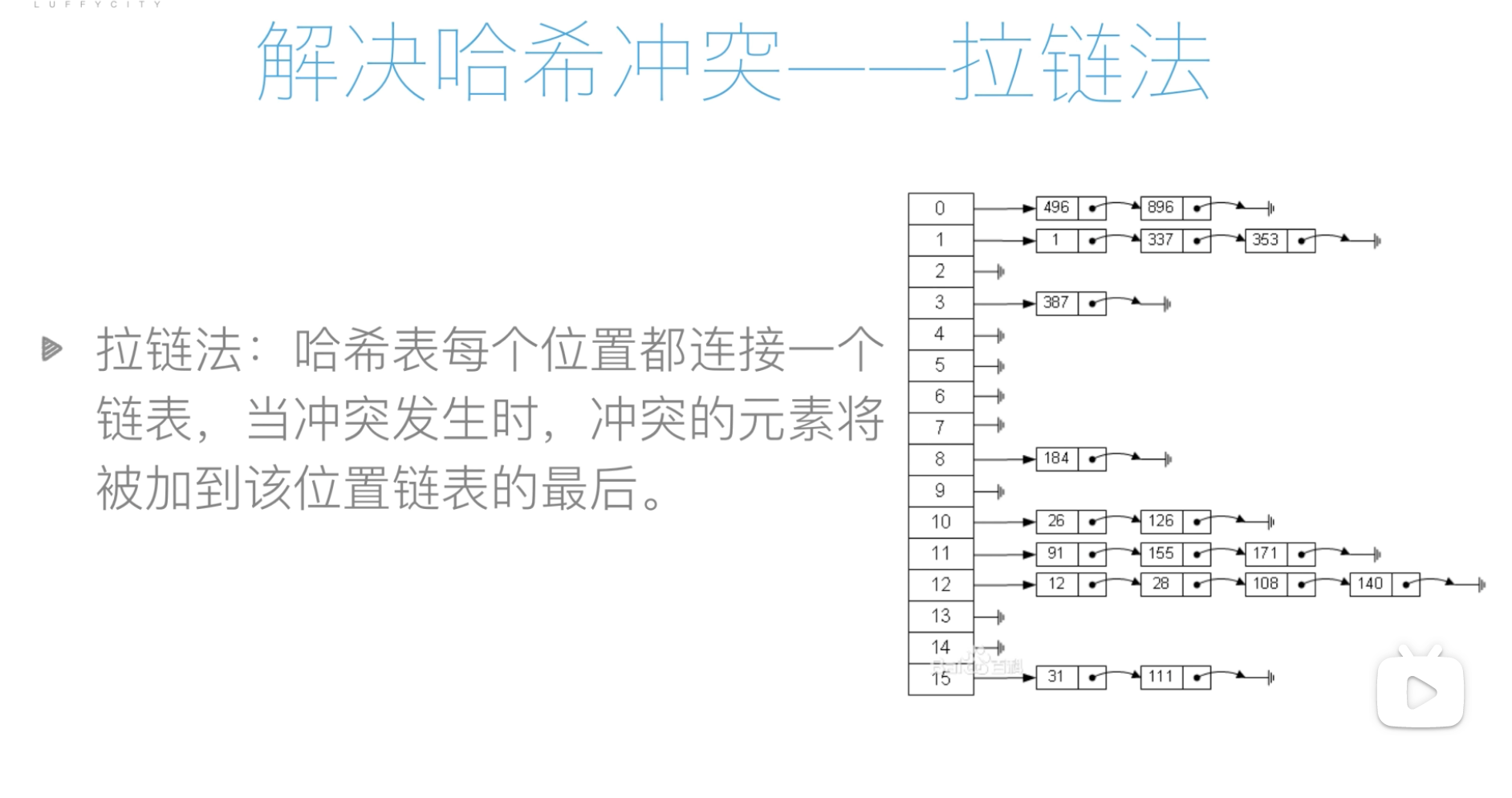
拉链法
直接寻址表
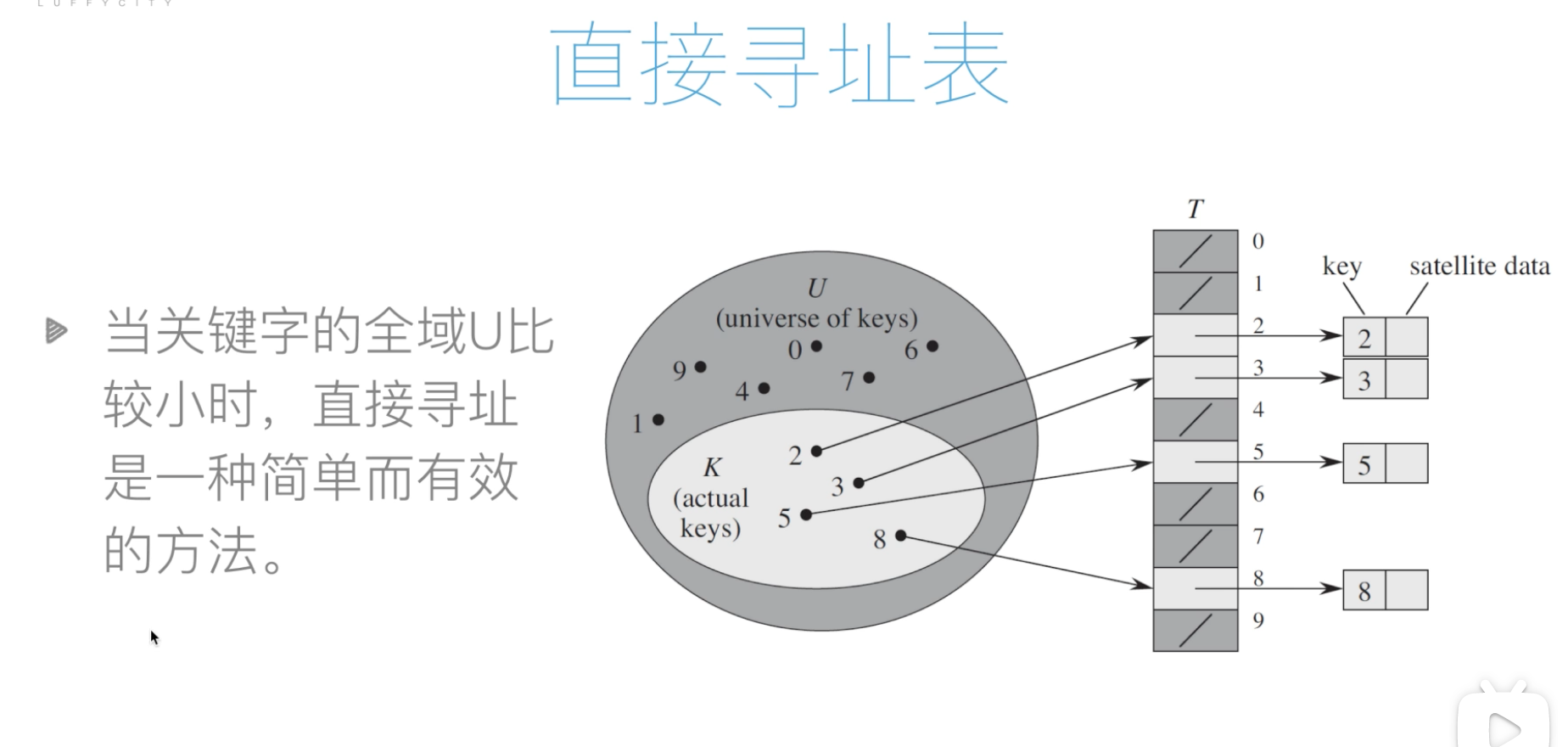
优缺点:
缺点:1.当域U很大时,需要消耗大量内存,很不实际2.如果域U很大而实际出现的key很少,则大量空间被浪费3.无法处理关键字不是数字的情况有点:1.查找快
常见的哈西函数

哈西表应用-md5算法


哈西表应用-SHA2算法

选择了IT,必定终身学习

