决策树学习记录

一。什么是决策树？让我们从养宠物开始说起~

 

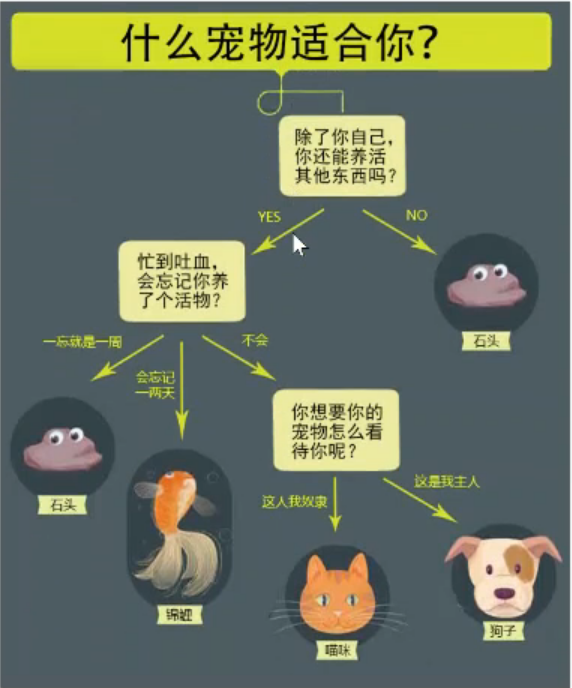
我们可以吧决策树看作是一个if-then规则的集合。将决策树转换成if-then规则的过程是这样的：

·有决策树的根节点到叶节点的每一条路径构建一条规则

·路径上中间节点的特征对应着规则的条件，也就是叶节点的标签对应着规则的结论

    决策树的路径或者其对应的if-then规则集合有一个重要的性质：互斥并且完备。也就是说，每一个实例都被有且仅有一条路径或者规则所覆盖。这里的覆盖是指实例的特征与路径上的特征一致

二。决策树的构建准备工作

使用决策树做分类的每一个步骤都很重要，首先我们要收集足够多的数据，如果数据集收集不到位，将会倒数没有足够的特征去构建错误率低的决策树。数据特征充足，但是不知道用哪些特征好，也会导致最终无法构建出分类效果好的决策树。从算法方面看的话，决策树的构建就是我们的核心内容。

决策树如何构建呢？通常，这一过程可以概括为3个步骤：特征选择，决策树的生成和决策树的剪枝。

1.特征选择

　　特征选择就是决定用哪个特征来划分特征空间，其目的在于选取对训练数据具有分类能力的特征。这样可以提高决策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大的差别，则称这个特征是没有分类能力的，经验上扔掉这些特征对决策树学习的精度影响不会很大。

那如何来选择最优的特征来划分呢？一般而言，随着划分过程不断进行，我们希望决策树的分支结点所包含的样本尽可能属于同一类别，也就是节点的纯度越来越高。

下面三个图表示的是纯度越来越低的过程，最后一个表示的是纯度最低的状态。

 

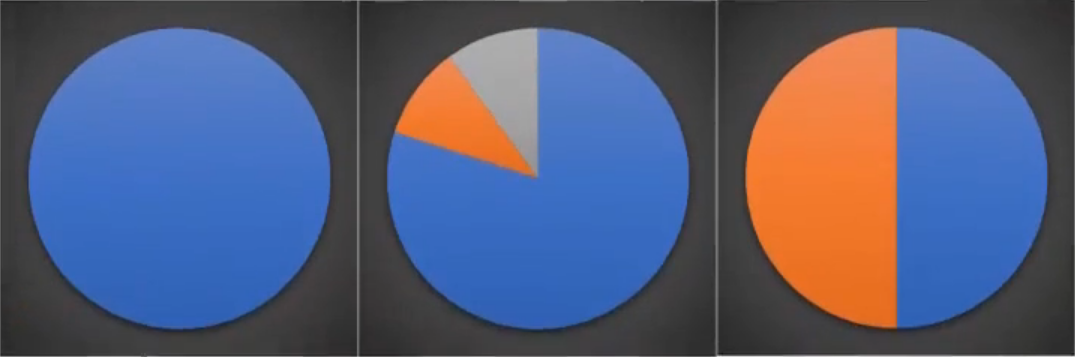
在实际使用中，我们衡量的常常是不纯度。度量不纯度的指标有很多种，比如：熵，增益值，基尼指数

 这里使用的是熵，也叫做香浓熵，这个名字来源于信息论之父 克劳德·香浓

1.1香浓熵及计算函数

熵定义为信息的期望值。在信息论与概率论统计中，熵表示随机变量不确定性的度量

假定当前样本集合d中有n类样本，第i类样本为xi，那么xi的信息定义为

　　 

通过上式，我们可以得到所有类别的信息。为了计算熵，我们需要计算所有类别所有可能值包含的信息期望值---数学期望，通过下面的公式得到

熵越大，d的不纯度越低

 

 

def calEnt(dataSet):
    n = dataSet.Shape[0]                        #数据集总行数
    iset = dataSet.iloc[:,-1].value_counts()    #标签的所有类别
    p = iset/n                                  #每一类标签所占比
    ent = (-p*np.log2(p)).sum()                 #计算信息熵
    return ent 

 

 

import numpy as np
import pandas as pd
def createDataSet():
    row_data = {'no surfacing':[1,1,1,0,0],'flipper':[1,1,0,1,1],'fish':['yes','yes','no','no','no']}
    dataSet = pd.DataFrame(row_data)
    return dataSet

 

1.2信息增益：

他的计算公式就是父节点的信息熵与旗下所有自己诶单总信息熵之差。需要注意的是，此时计算子节点的总信息熵不能简单求和，而要求在求和汇总之前进行修正。

假设离散属性a有V个可能的取值｛a1，a2,.....,av｝,若使用a对样本数据集D进行划分，则会产生V个分支节点，其中第V个分支节点包含了D中所有在属性a上取值为av的样本，记为Dv，我们可根据信息熵的计算公式计算出Dv的信息熵，再考虑到不同的分支节点包含的样本数不同，给分支节点赋予权重|Dv|/|D|，这就是所谓的修正。

所以信息增益的计算公式为：

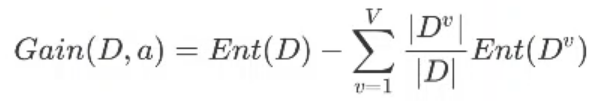
结果：

同样的方法，可以把第一列的信息增益也算出来，结果为0.17

2.数据集最佳切分函数

划分数据集的最大准则是选择最大信息增益，也就是信息下降最快的方向。（也就是最快到达叶节点，最快的生长速度）

 

"""
函数功能：根据信息增益选择出最佳数据集切分的列
函数说明：
    dataSet:原始数据集
返回：
    axis：数据集最佳切分列的索引
"""
def bestSplit(dataSet):
    baseEnt = calEnt(dataSet)                  #计算原始熵
    bestGain = 0                               #初始化信息增益
    axis = -1                                 #初始化最佳切分列，标签列
    for i in range (dataSet.shape[1]-1):     #对特征的每一列进行循环
        levels = dataSet.iloc[:,i].value_counts().index     #提取出当前的所有取值
        ents = 0                                             #初始化子节点的信息熵
        for j in levels:                                    #对当前列的每一个取值进行循环
            childSet = dataSet[dataSet.iloc[:i] == j]     #某一个子节点的dataframe
            ent = calEnt(childSet)                       #计算某一个子节点的信息熵
            ents += (childSet.shape[0]/dataSet.shape[0])*ent    #计算当前列的信息熵
            #print(f'第{i}列的信息熵为{ents}')
            infoGain = baseEnt - ents                    #计算当前列的信息增益
            #print(f'第｛i｝列的信息增益为｛infoGain｝')
            if(infoGain > bestGain):
                bestGain = infoGain                   #选择最大信息增益
                axis = i                              #最大信息增益所在的列的索引
            return axis

3.按照给定列来切分数据集

通过最佳切分函数返回最佳切分列的索引，我们就可以根据索引，构建一个按照给定列切分数据集

 

"""
函数功能：按照给定的列划分数据集
函数说明：
    dataSet:原始数据集
    value：指定的属性值
返回：
    redataSet：按照指定列索引的属性值切分后的数据集
"""
def mysplit(dataSet,axis,value):
    col = dataSet.columns[axis]
    redataSet = dataSet.loc[dataSet[col]==value,:].drop(col,axis = 1)
    return redataSet
axis  = 0
value = 1

mysplit(dataSet,0,1)

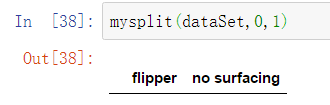
三。递归构建决策树

目前我们已经学习了从数据集构造决策树算法所需要的子功能模块，其工作原理如下：得到原始数据集，然后基于最好的属性值划分数据集，由于特征值可能多于两个，因此可能存在大于两个分支的数据集划分。第一次划分之后，数据集被向下传递到树的分支的下一个节点。在这个节点上，我们可以再次划分数据。因此我们可以采用递归的原则处理数据集

决策树生成算法递归地产生决策树，直到不能继续下去为止。这样产生的树往往对训练数据的分类很准确，但对未知的测试数据的分类却没有那么准确，即出现过拟合现象。过拟合的原因在于学习时过多地考虑如何提高对训练数据的正确分类，从而构建出过于复杂的决策树。解决这个问题的办法是考虑决策树的复杂性，对已生成的决策树进行简化，也就是常说的剪枝处理。（剪枝又分为自下而上和自上而下两种方法）

1.ID3算法

构建决策树的方法有很多，比如ID3，c4.5和Cart，基于《机器学习实战》这本书，我们选择ID3算法。

ID3算法的核心是在决策树各个节点上对应信息增益准则选择特征，递归地构建决策树。具体方法是：从根节点开始，对节点计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的特征，由该特征的不同取值建立子节点；再对子节点递归地调用以上方法，构建决策树；直到所有特征的信息增益均很小或没有特征可以选择为止。最后得到一个决策树。

递归结束的条件是：程序遍历完所有的特征列，或者每个分支下的所有实例都具有相同的分类。如果所有实例都具有相同的分类，则得到一个叶节点。任何到达叶节点的数据必然属于叶节点的分类，即叶节点里面必须是标签。

"""
函数功能：基于最大信息增益切分数据集，递归构建决策树
参数说明：
    dataSet：原始数据集（最后一列是标签）
返回：
    myTree：字典形式的树

    
"""
def createTree(dataSet):
    featlist = list(dataSet.columns)                        #提取出数据集所有的列
    classlist = dataSet.iloc[:,-1].value_counts()           #获取最后一列类标签
    #判断最多标签数目是否等于数据集行数，或者数据集是否只有一列
    if classlist[0] == dataSet.shape[0] or dataSet.shape[1] == 1:
        return classlist.index[0]                           #如果是，返回类标签
    axis = bestSplit(dataSet)                               #确定出当前最佳且分列的索引
    bestfeat = featlist[axis]                               #获取该索引对应的特征
    myTree = {bestfeat:{}}                                  #采用字典嵌套的方式存储树信息
    del featlist[axis]                                      #删除当前特征
    valuelist = set(dataSet.iloc[:,axis])                    #提取最佳切分列所有属性值
    for value in valuelist:                                 #对每一个属性值递归建树
        myTree[bestfeat][value] = createTree(mySplit(dataSet,axis,value))
    return myTree
    

四。决策树的存储

构造决策树是很耗时的任务，即使处理很小的数据集，也要花费几秒的时间，如果数据集很大，将会耗费很多计算时间。因此为了节省时间，建好树之后立马将其保存，后续使用直接调用即可。

这里使用的是numpy里面的save（）函数，它可以直接把字典形式的数据保存为.npy文件，调用的时候直接使用load（）函数即可。

#树的存储
np.save('myTree.npy',myTree)
#树的读取
read_myTree = np.load('myTree.npy').item()
read_myTree

五。使用决策树执行分类

def classify(inputTree,labels, testVec):
    firstStr = next(iter(inputTree)) #获取决策树第一个节点
    secondDict = inputTree[firstStr] #下一个字典
    featIndex = labels.index(firstStr) #第一个节点所在列的索引
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]) == dict :
                classLabel = classify(secondDict[key], labels, testVec)
            else:
                classLabel = secondDict[key]
    return classLabel

未完待续。。。

 总结！！！

决策树的流程：

1.特征选择 

　　1.1香浓熵及计算函数

　　1.2信息增益

2.数据集最佳切分函数

3.递归构建决策树（ID3算法（信息增益），c4.5算法，cart算法）

4.决策树的存储（numpy包）

5.使用决策树执行分裂

6.决策树可视化（叶子节点数据，树的深度，绘制节点，标注有向边属性值）