其它 以字典的方式 暴力破解 压缩文件密码
文章看完后,还是不太懂的,可加群讨论、互助,QQ群号:762257978
背景
以前加密了一个压缩文件,里面全是回忆的照片,结果密码搞忘记了,我勒个去,然后就在网上下载了个软件暴力破解,结果很明显,没有破解出来。然后自己就思索怎么破解。
一开始是加QQ群,让别人帮忙破解,仍然没有破解出来,别个还帮我跑了100g的字典,还是挺感谢他的,再说一声 谢谢了哈,没有收我钱,全凭热心。
然后自己就寻思着,看怎么破解,暴力破解估计没戏,除非搭建云,用N多电脑协同破解,这方法对我而言不可取。
接着就想,还是字典破解吧,然后字典就很重要了撒,聪明的黑客,不可能什么都暴力破解,肯定会根据用户信息,生成特定的密码,这样破解的概率是最大的。这压缩文件的密码又是我自己设定的,那么根据我的习惯得出自己的密码应该还是不难,就在网上找生成密码的算法,其实就是个数学里面的排列组合,用C#实现。然后就是把密码给搞出来,把常用密码拆分一下就可以了,根据自己的习惯来。比如,我喜欢用guxingyue这个密码,然后我就拆分为gu、xing、yue,还有喜欢用guxingy这个密码,这密码是一个整体
下面是我的原始字典

经过排序组合,变成这个样子:
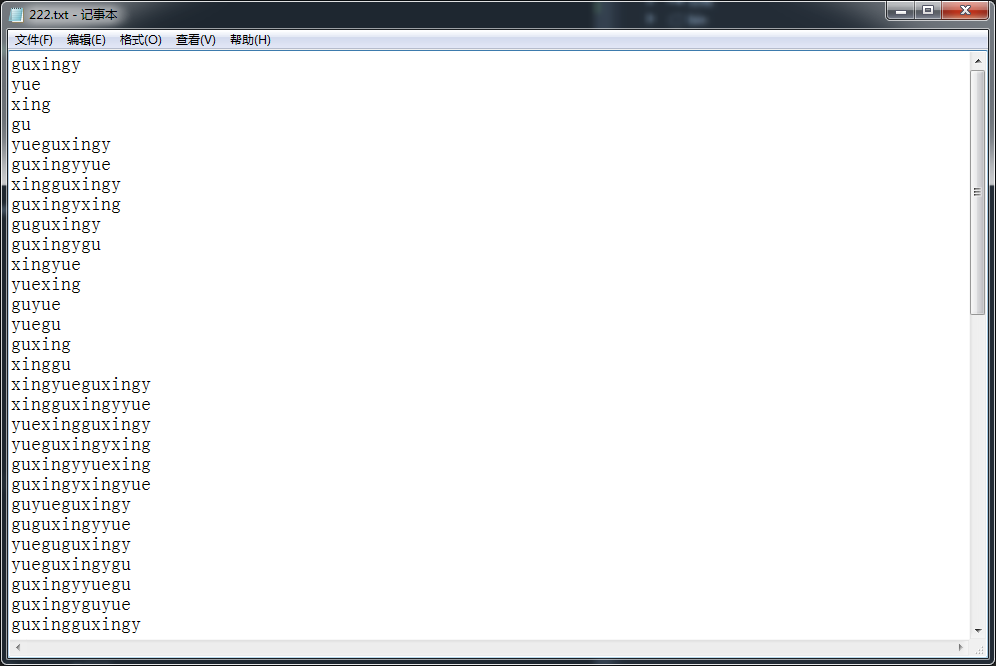
解释一下哈,有1个密码的组合,有2个密码的组合,有3个密码的组合,有4个密码的组合排列。总共就只有4个最基本的密码。

生成的密码数量就是这样多。
这样生成后的密码,就可以做为字典用于暴力破解了。
排列组合的原文链接:https://www.cnblogs.com/kissdodog/p/5419981.html
用到的代码:
1、排列组合:

public class PermutationAndCombination<T> { /// <summary> /// 交换两个变量 /// </summary> /// <param name="a">变量1</param> /// <param name="b">变量2</param> public static void Swap(ref T a, ref T b) { T temp = a; a = b; b = temp; } /// <summary> /// 递归算法求数组的组合(私有成员) /// </summary> /// <param name="list">返回的范型</param> /// <param name="t">所求数组</param> /// <param name="n">辅助变量</param> /// <param name="m">辅助变量</param> /// <param name="b">辅助数组</param> /// <param name="M">辅助变量M</param> private static void GetCombination(ref List<T[]> list, T[] t, int n, int m, int[] b, int M) { for (int i = n; i >= m; i--) { b[m - 1] = i - 1; if (m > 1) { GetCombination(ref list, t, i - 1, m - 1, b, M); } else { if (list == null) { list = new List<T[]>(); } T[] temp = new T[M]; for (int j = 0; j < b.Length; j++) { temp[j] = t[b[j]]; } list.Add(temp); } } } /// <summary> /// 递归算法求排列(私有成员) /// </summary> /// <param name="list">返回的列表</param> /// <param name="t">所求数组</param> /// <param name="startIndex">起始标号</param> /// <param name="endIndex">结束标号</param> private static void GetPermutation(ref List<T[]> list, T[] t, int startIndex, int endIndex) { if (startIndex == endIndex) { if (list == null) { list = new List<T[]>(); } T[] temp = new T[t.Length]; t.CopyTo(temp, 0); list.Add(temp); } else { for (int i = startIndex; i <= endIndex; i++) { Swap(ref t[startIndex], ref t[i]); GetPermutation(ref list, t, startIndex + 1, endIndex); Swap(ref t[startIndex], ref t[i]); } } } /// <summary> /// 求从起始标号到结束标号的排列,其余元素不变 /// </summary> /// <param name="t">所求数组</param> /// <param name="startIndex">起始标号</param> /// <param name="endIndex">结束标号</param> /// <returns>从起始标号到结束标号排列的范型</returns> public static List<T[]> GetPermutation(T[] t, int startIndex, int endIndex) { if (startIndex < 0 || endIndex > t.Length - 1) { return null; } List<T[]> list = new List<T[]>(); GetPermutation(ref list, t, startIndex, endIndex); return list; } /// <summary> /// 返回数组所有元素的全排列 /// </summary> /// <param name="t">所求数组</param> /// <returns>全排列的范型</returns> public static List<T[]> GetPermutation(T[] t) { return GetPermutation(t, 0, t.Length - 1); } /// <summary> /// 求数组中n个元素的排列 /// </summary> /// <param name="t">所求数组</param> /// <param name="n">元素个数</param> /// <returns>数组中n个元素的排列</returns> public static List<T[]> GetPermutation(T[] t, int n) { if (n > t.Length) { return null; } List<T[]> list = new List<T[]>(); List<T[]> c = GetCombination(t, n); for (int i = 0; i < c.Count; i++) { List<T[]> l = new List<T[]>(); GetPermutation(ref l, c[i], 0, n - 1); list.AddRange(l); } return list; } /// <summary> /// 求数组中n个元素的组合 /// </summary> /// <param name="t">所求数组</param> /// <param name="n">元素个数</param> /// <returns>数组中n个元素的组合的范型</returns> public static List<T[]> GetCombination(T[] t, int n) { if (t.Length < n) { return null; } int[] temp = new int[n]; List<T[]> list = new List<T[]>(); GetCombination(ref list, t, t.Length, n, temp, n); return list; } }
2、生成密码:

public void test4() { //排列组合 生成密码 StringBuilder sb = new StringBuilder(); var strContent = System.IO.File.ReadAllText("02 pwd.txt"); List<string> list = Regex.Split(strContent, "\r\n").ToList();//一个sheet包含的所有行,行与行之间用回车分隔 //这里的1234,就是组合的个数 new List<int> { 1, 2, 3, 4 }.ForEach(num => { List<string[]> ListCombination = PermutationAndCombination<string>.GetPermutation(list.ToArray(), num); //求全部的3-3组合 foreach (var arr in ListCombination) { string pwd = "";//排列组合后的密码 foreach (var item in arr) { pwd += item; } sb.Append(pwd + "\r\n"); } Console.WriteLine($"num:{num} count:{ListCombination.Count}"); }); System.IO.File.WriteAllText("222.txt", sb.ToString()); }
文件解释:
02 pwd.txt 里面存的是最基本的密码,就是用于组合排列的那几个基本元素,数学里面叫什么忘记了,突然感觉高中就像白学了一样,这都能忘!!还是没有经常用到的缘故吧
222.txt 里面存的是排序组合后的密码
用到的破解工具:
都是百度搜索的,这里鄙视一下百度,搜索经常是广告一连串,真是无聊。简直跟谷歌无法比,谷歌游览器装个插件一样能用谷歌搜索,这个插件叫:谷歌访问助手,不是打广告,好用的东西要分享,我也是我们公司的跟我讲才知道的,一直都以为需要挂vpn才能FQ,游览器装个插件就可以了,关键是还免费。
ARPR_gr(我用的是这个哈 在电脑上找到的 都不知道什么时候下载的 破解类型 选择字典破解,不要选暴力破解哈)
补充:Advanced RAR Password Recovery(ARPR)
Advanced Office Password Recovery (这个之前下来是准备破解Excel密码的,我哥哥的Excel密码忘记了,找我,然后下的)
hashcat (这个是之前 那个群里的好人 帮我破解用的软件,他因为帮我免费破解,估计是抢了群主的生意,群主还把他踢了,唉 不想说什么 挺感谢的 哥们)
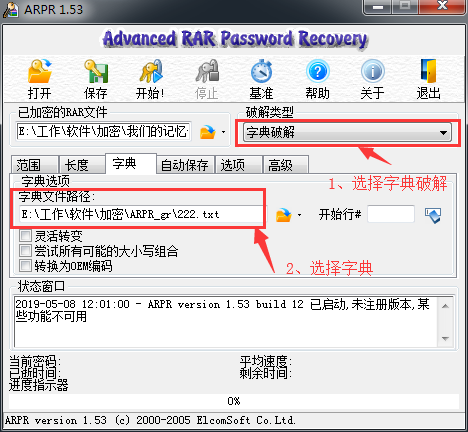
最后再说一下哈,我不是教别个破解。只是自己遇到了忘记密码,把自己的破解过程记录一下。还有就是现在很多破解的群好坑,其它的不想多说
具体的操作步骤:
之前公司的电脑硬盘坏了,就当重新复习一下吧
压缩文件地址:https://files-cdn.cnblogs.com/files/guxingy/%E7%94%A8%E7%BB%84%E5%90%88%E6%8E%92%E5%88%97%E7%9A%84%E6%96%B9%E5%BC%8F%E9%87%8D%E6%96%B0%E6%9E%84%E5%BB%BA%E5%AF%86%E7%A0%81.rar
复制到迅雷里面下载就可以了,或者直接点击“压缩文件地址”这几个字就可以了
下载之后解压一下,看下图的说明:
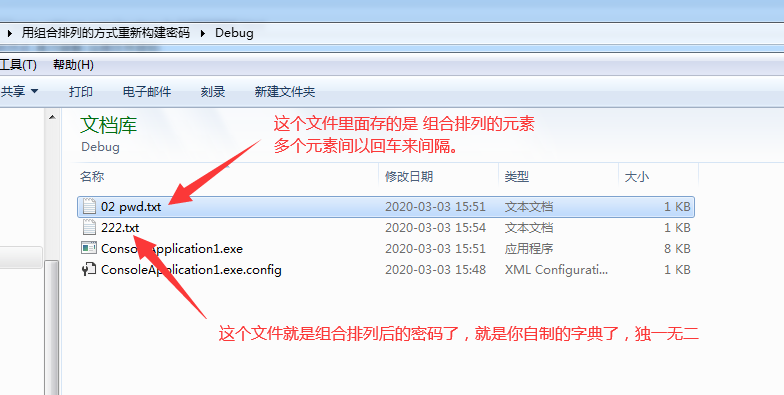
一、生成字典的步骤:
1、下载压缩文件
2、解压文件
3、打开文件“02 pwd.txt”,编写自己的密码元素,每个密码元素以“回车”隔开
4、执行文件“ConsoleApplication1.exe”
5、文件“222.txt”就是生成的密码字典了
二、使用密码字典的步骤:
1、软件下载:https://pan.baidu.com/share/link?shareid=3379506451&uk=1076102322
百度网盘里面的 直接就可以下 也是百度搜的 可惜是英文版 下次找到中文版了 就把链接补上
怕百度网盘的链接失效,在补上一个,https://files-cdn.cnblogs.com/files/guxingy/ARPR_4.53.rar
2、准备一个需要解密的压缩文件,用于测试
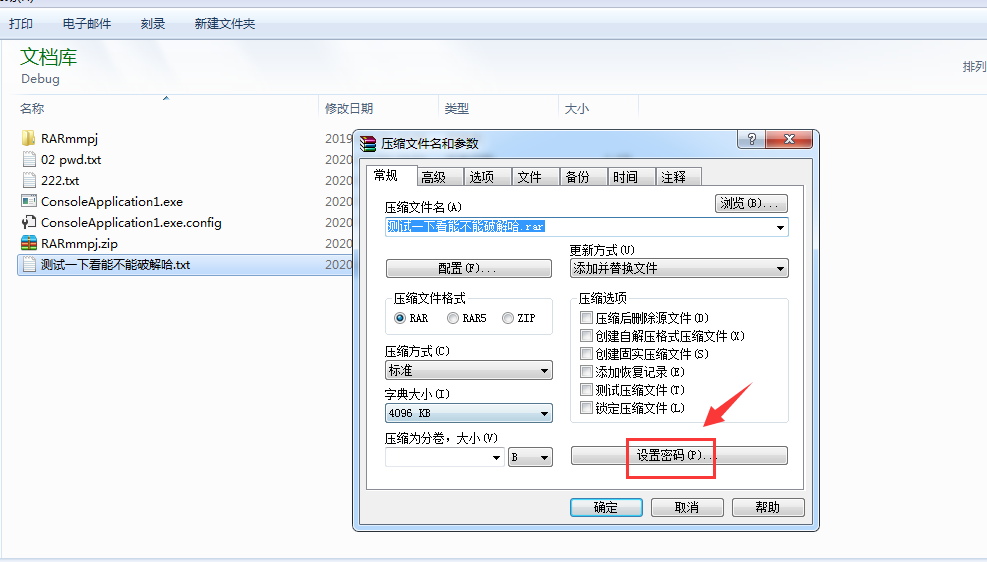
3、解压文件“ARPR_4.53.rar”,找到文件“archpr.exe”,双击打开
在选择过程中,如果就执行了破解了,你就点一下“Stop”就可以了,
等全部选择好后,再点一下“Start”就可以了。
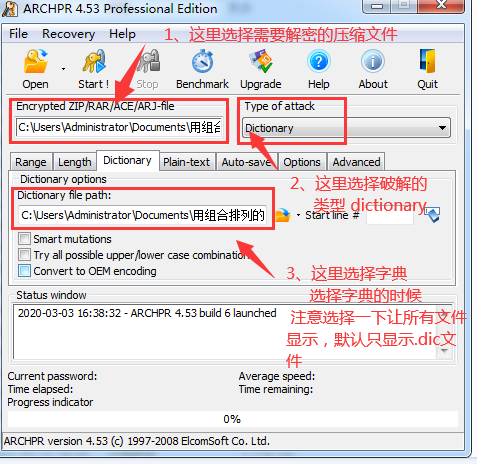
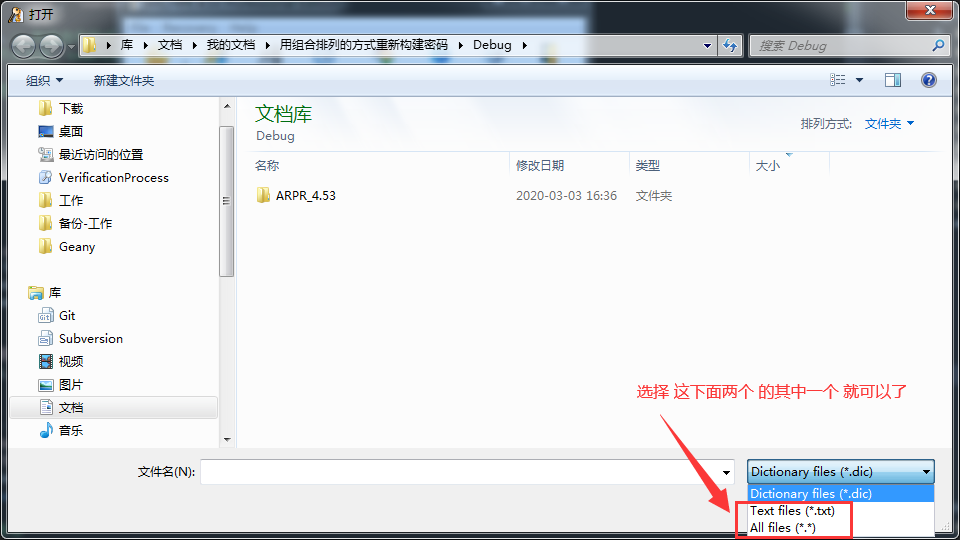
5、破解成功后会出现这个界面:
这种方式破解的关键在于字典的精准程度,你需要把自己的基础密码整理好,程序仅仅只是帮你组合排列密码给。
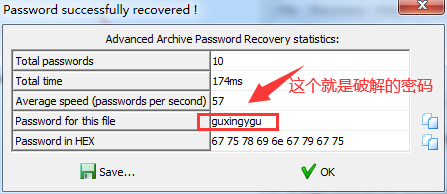
6、最后附上程序的源码,代码其实都贴出来的,用vs2015+就可以打开了:
https://files-cdn.cnblogs.com/files/guxingy/%E7%94%A8%E7%BB%84%E5%90%88%E6%8E%92%E5%88%97%E7%9A%84%E6%96%B9%E5%BC%8F%E9%87%8D%E6%96%B0%E6%9E%84%E5%BB%BA%E5%AF%86%E7%A0%81-%E6%BA%90%E7%A0%81.rar





