算法基础一 左移、右移、正数、负数
如何将一个int数值的三十二位二进制数字打印出来?这里就要用到左移
首先理解&字符,&字符的左右两端如果都为数值,会转换成二进制去进行运算。
比如 12&5 12转成二进制数是1100(前四位省略了),5转成二进制数是0101,则运算后的结果为0100即4

也就是说他会每一位的去比对, 1 1为1 1 0为0,0 0为0
所以当一个num想要知道他的二进制的时候可以这样

因为&的两边都会成为二进制,我们先不管num是啥,1的二进制是00000000......00001,只有最后面的第一位是1,其他的都是0,
然后根据上面代码,让1左移31位,也就成了1.........0000000,最后一位是1,其他的都是0,然后与num比较,因为1的前31位都是0了,所以运算后的前31位肯定也就都是0了,以为二进制只有0和1,一边已经是0了,无论num是啥,前三十一为都是0,关键就在第三十二位1上,假如num的三十二位也是1,那么运算后的结果也是1,也就是上面代码的结果不等于0,所为我们输出1,假如num的三十二位是0,运算后的三十二位也是0,上面的代码结果等于0,我们输出0,这样一个num的三十二位二进制数就被输出了。
怎么看二进制?
二进制第一位代表的是2的0次方,第二位是2的1次方,哪个位置有1,就把哪个位置的2的次方相加,就得到十进制的数了。
比如1是0000000000000001

这个代表的就是2的0次方,是1.
比如3是000000000000011;代表的意思就是2的0次方+2的1次方等于3
整数范围是-2的31次方+1-------2的31次方
正数的二进制一共有32位,0-30位是用来表示数值的,最高位31位是符号为,0表示非负数,1表示负数。
负数在底层表示为正数取反加1
比如1的二进制是这样的。
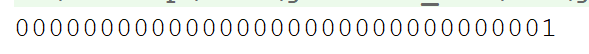
-1的二进制就是

符号为变成1,其他的取反,变成11111111111110让后加了1,就变成11111111111111.
之所以要这么设计,是为了底层在进行加减乘除的时候,无论数值是正还是负,都用一套逻辑。比如-a, a无论是正数还是负数,都可以用取反加1这套逻辑,结果都是正确的。
但是要注意,如果是最小数取反加一,还是他自己,因为负数最小值是

取反就都是1111111111111111111111,在加1,然后进位,又变成了1000000000000000000,所以负数的最小值取反还是他自己,0取反还是0



