求斐波那契数列的第n项
问题描述:斐波那契数列是这样的一个数列,1,1,2,3,5,8,..,即前两项都是1,后面每一项都是其前面两项的和。
现在要你求出该数列的第n项。
分析:该问题是一个经典的数列问题,相信大家在很多语言的教科书上都碰到过这个练习题目。这里我给大家总结了三种经典解法,并对这三个方法进行了对比。
解法一:递归算法。很多教科书上都用这个题作为函数递归知识点讲解的例题,我们可以将每一个项的求法表达为这样一个式子:
f(n)=f(n-1)+f(n-2),f(1)=1,f(2)=1,可以看出,可以采用递归算法求解。
解法二:循环求法。我们可以从第1项开始,一直求到第n项,即可,一个循环可以做到,时间复杂度为O(n).
解法三:矩阵链乘法。如果线性代数学的好的话,可以想出这样一种解法,

同样可以采用递归的算法求解,时间复杂度为O(logn).
三种解法对比:解法一编程最简单,但是效率最低,因为这种递归算法求解时,会重复求解子问题。如下图示:
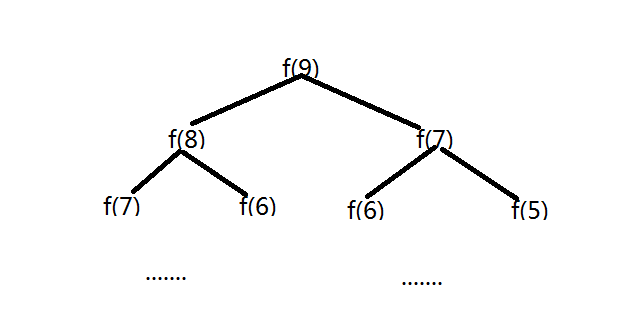
这样就看出来吧!另外如果n很大的话,递归的层数很大,会消耗系统大量的时间和资源。
解法二避免了重复求解子问题,线性时间即可求出,值得采用。
解法三效率最高,但是编程特别复杂,在有些情况下,很合适使用,但就本题目来说,推荐解法二。
针对上述三种解法,我给出了详细的Java代码,读者可以参考:
1 import java.util.*; 2 public class Main { 3 public static int f1(int n){ //方法一:递归算法,自底向上 4 if(n<=2)return 1; //如果是求前两项,直接返回就可 5 else return f1(n-1)+f1(n-2); 6 } 7 public static int f2(int n){ //方法二:循环算法,自上而下 8 if(n<=2)return 1; //如果是求前两项,直接返回就可 9 int a1=1,a2=1,a3; 10 for(int i=3;i<=n;i++) 11 { 12 a3=a1+a2; 13 a1=a2; 14 a2=a3; 15 } 16 return a2; 17 } 18 public static int[][] f3(int n){ //方法三:矩阵链相乘算法,采用递归实现 19 int a[][]={{1,1},{1,0}}; //定义基矩阵 20 int b[][]; //存储子方法的结果 21 int c[][]=new int[2][2]; //存储最后计算结果 22 int d[][]=new int[2][2]; //存储中间计算结果 23 if((n)<=1)return a; //如果次方小等于1直接返回 24 else if((n) %2==1) 25 {b=f3((n-1)/2); 26 27 d[0][0]=b[0][0]*b[0][0]+b[0][1]*b[1][0]; 28 d[0][1]=b[0][0]*b[0][1]+b[0][1]*b[1][1]; 29 d[1][0]=b[1][0]*b[0][0]+b[1][1]*b[1][0]; 30 d[1][1]=b[1][0]*b[0][1]+b[1][1]*b[1][1]; 31 32 c[0][0]=d[0][0]*a[0][0]+d[0][1]*a[1][0]; 33 c[0][1]=d[0][0]*a[0][1]+d[0][1]*a[1][1]; 34 c[1][0]=d[1][0]*a[0][0]+d[1][1]*a[1][0]; 35 c[1][1]=d[1][0]*a[0][1]+d[1][1]*a[1][1]; 36 37 } 38 else { 39 b=f3((n)/2); 40 41 c[0][0]=b[0][0]*b[0][0]+b[0][1]*b[1][0]; 42 c[0][1]=b[0][0]*b[0][1]+b[0][1]*b[1][1]; 43 c[1][0]=b[1][0]*b[0][0]+b[1][1]*b[1][0]; 44 c[1][1]=b[1][0]*b[0][1]+b[1][1]*b[1][1]; 45 } 46 return c; 47 } 48 public static void main(String[] args) { 49 // TODO 自动生成的方法存根 50 Scanner scan=new Scanner(System.in); 51 int n=scan.nextInt(); 52 System.out.println("方法一:"+f1(n)); 53 System.out.println("方法二:"+f2(n)); 54 int a[][]=f3(n-1); //因为是要求矩阵{{1,0},{1,0}}的n-1次方 55 System.out.println("方法三:"+a[0][0]); 56 57 } 58 59 }
输出结果为:
10
方法一:55
方法二:55
方法三:55



