最长公共子序列问题

输入：两个字符串序列

输出：两个字符串序列的最长公共子序列的长度和子序列

例如：

输入：str1="BDCABA",   str2="ABCBDAB"

输出：4   “BDAB”

若此问题采用暴力法求解：枚举str1的每个子序列str，检查str是否为序列str2的子序列，记录当前找到的长度的最大的公共子序列。可以看出暴力法的效率十分低下，并且每次检查str是否为str2的子序列的时间复杂度为O(n),然而str有2^m 个子序列，因此采用暴力法的最坏时间复杂度为O(n2^m)。

针对此问题可以采用动态规划去做。

令C[i,j]表示str1的前i项和str2的前j项的最长公共子序列的长度，则会有

计算长度算法为LcsLength

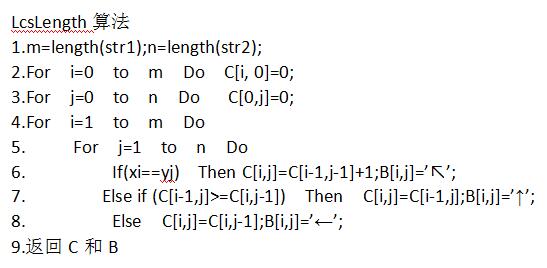
打印最长公共子串的算法为LcsPrint

用Java语言的具体实现代码如下：

public class LcsLength {
    public static int lcslength(String str1,String str2,char b[][]){
        int m=str1.length();
        int n=str2.length();
        int c[][]=new int[m+1][n+1];                               //统计长度
        
        for(int i=0;i<=m;i++)c[i][0]=0;
        for(int j=0;j<=n;j++)c[0][j]=0;
        for(int i=1;i<=m;i++)
            for(int j=1;j<=n;j++)
                if(str1.charAt(i-1)==str2.charAt(j-1)){c[i][j]=c[i-1][j-1]+1;b[i][j]='X';}    //X表示左上箭头
                else if(c[i-1][j]>=c[i][j-1]){c[i][j]=c[i-1][j];b[i][j]='U';}                 //U表示向上箭头
                else {c[i][j]=c[i][j-1];b[i][j]='L';}                                         //L表示向左箭头
        return c[m][n];                                                                      //返回最长子序列的长度
    }
    
    public static void lcsprint(char B[][],String str1,int m,int n){
        if(m==0||n==0)return;
        if(B[m][n]=='X'){lcsprint(B,str1,m-1,n-1);System.out.print(str1.charAt(m-1));}
        else if(B[m][n]=='U')lcsprint(B,str1,m-1,n);
        else lcsprint(B,str1,m,n-1);
    }
    
    public static void main(String[] args) {
        // TODO 自动生成的方法存根
        String str1 = new String("BDCABA");
        String str2 = new String("ABCBDAB");
        System.out.println("第一个字符串str1为："+str1);
        System.out.println("第二个字符串str2为："+str2);
        int m=str1.length();
        int n=str2.length();
        char B[][]=new char[m+1][n+1];
        System.out.println("最长公共子序列的长度为："+lcslength(str1,str2,B));
        System.out.print("最长公共子序列为：");
        lcsprint(B,str1,m,n);

    }

}

输出为：

第一个字符串str1为：BDCABA
第二个字符串str2为：ABCBDAB
最长公共子序列的长度为：4
最长公共子序列为：BDAB