外部排序（归并排序）

外部排序（归并排序）

定义

基本思想及步骤

　　步骤

 

　　1.思想 一

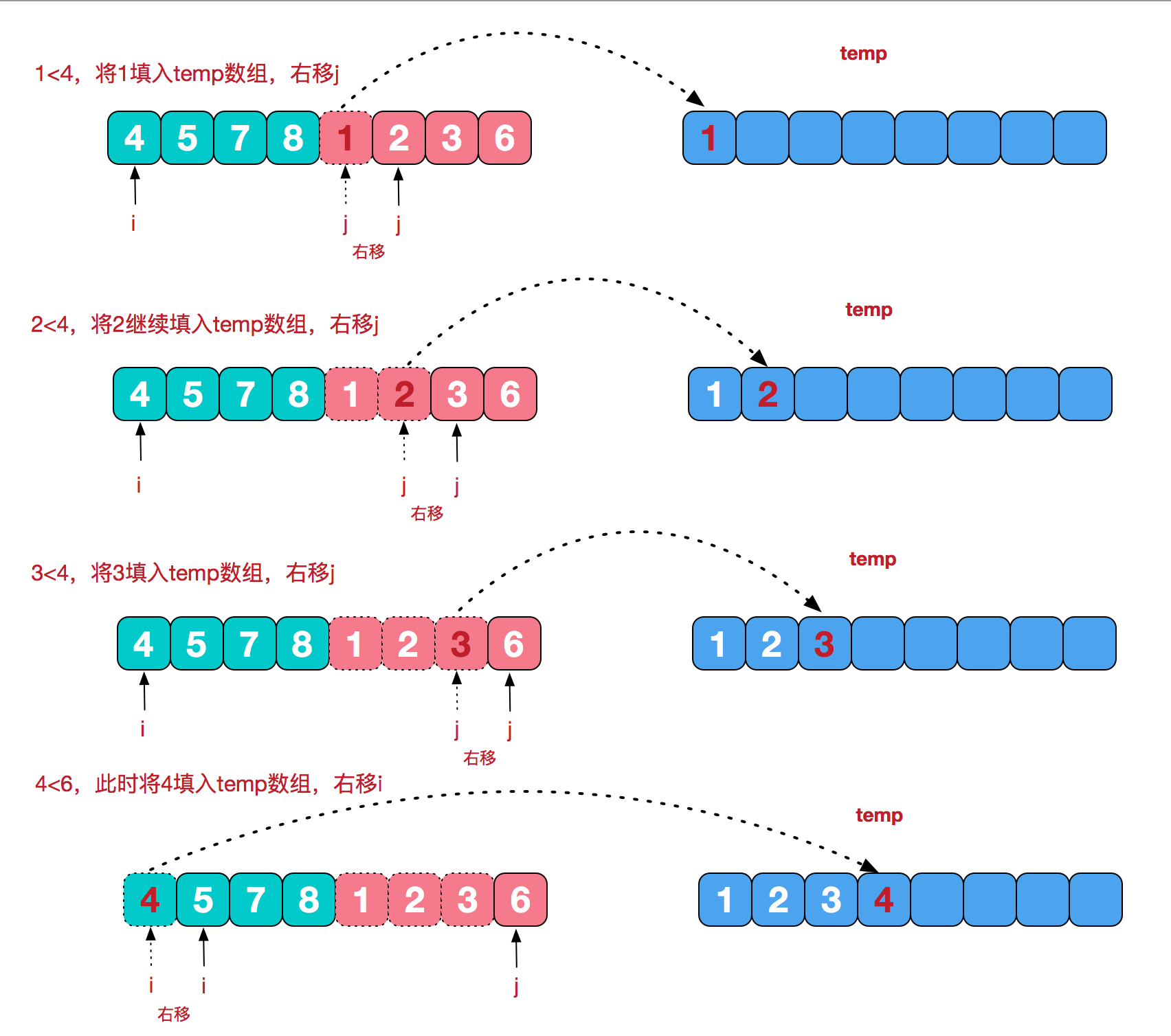
　　2.思想 二

 

 

 

　　　　　　　　

 

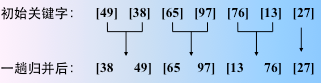
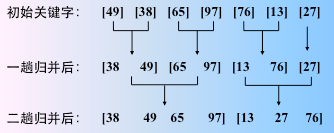
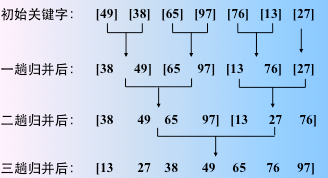
 实现操作

　　1.二路归并　　

　　1.1.c 

递归

//二路一次归并过程的算法
//low为本次二路归并排序的第1有序区的第1个元素，i指向第1个元素, mid为第1有序区的最后1个元素
void merge(int List[], int low, int mid, int high)
{
    //mid+1为第2有序区第1个元素，mid为第1有序区的最后1个元素
    //i 指向第 1 有序区的第 1 个元素
    int i = low;
    //j 指向第 2 有序区的第 1 个元素，high 为第 2 有序区的最后一个元素
    int j = mid + 1;
    //temp数组暂存合并的有序序列
    int *temp = new int[high - low + 1];
    //设置临时数组的指示标志 k
    int k = 0;
    //内存分配失败
    if(!temp){
        cout<<"数组分配失败！";
        exit(0);
    }
    //顺序选取两个有序区的较小元素，存储到t数组中，因为是递增排序
    while(i <= mid && j <= high){
        //较小的元素，存入temp临时数组中
        if(List[i] <= List[j]){
            temp[k++] = List[i++];
        }else{
            temp[k++] = List[j++];
        }
    }// end of while
    //比完之后，假如第1个有序区仍有剩余，则直接全部复制到 temp 数组
    while(i <= mid){
        temp[k++] = List[i++];
    }
    //比完之后，假如第2个有序区还有剩余，则直接全部复制到 temp 数组
    while(j <= high){
        temp[k++] = List[j++];
    }
    //将排好序的序列，重存回到 list 中 low 到 high 区间
    for(i = low, k = 0; i <= high; i++, k++){
        List[i] = temp[k];
    }
    //delete [] 删除动态数组的内存
    delete []temp;
}

//递归实现二路归并排序（也就是分治法的思想）
void mergeSort(int List[], int low, int high)
{
    //二路归并排序，分为二路
    int mid = (low + high) / 2;
    //终止条件，low >= high， 不是while，且不含等号，否则死循环
    if(low < high)
    {
        //递归过程，二路归并排序递归过程
        mergeSort(List, low, mid);
        mergeSort(List, mid + 1, high);
        //归并
        merge(List, low, mid, high);
    }
}

int main(void)
{
    int source[7] = {49, 38, 65, 97, 76, 13, 27};
    
    mergeSort(source, 0, 6);
    
    for (int i = 0; i < 7; i++) {
        printf(" %d  ", source[i]);
    }
    
    return 0;
}

 

非递归

//非递归算法实现二路归并排序，length代表数组长度，即数组最大下标是 legth - 1
void mergeSort(int List[],int length)
{
    //回忆图解的过程，二路归并算法的流程，不同于递归，递归是先递归语句，然后归并函数，这样归并函数是倒序执行（和递归函数执行顺序相反）
    int size = 1;
    int low;
    int mid;
    int high;
    //size 是标记当前各个归并序列的high-low，从1，2，4，8，……，2*size
    while(size <= length - 1)
    {
        //从第一个元素开始扫描，low代表第一个分割的序列的第一个元素
        low = 0;
        //当前的归并算法结束的条件
        while(low + size <= length - 1)
        {
            //mid代表第一个分割的序列的最后一个元素
            mid = low + size - 1;
            //high 代表第二个分割的序列的最后一个元素
            high = mid + size;
            //判断一下：如果第二个序列个数不足size个
            if(high > length - 1){
                //调整 high 为最后一个元素的下标即可
                high = length - 1;
            }
            //调用归并函数，进行分割的序列的分段排序
            merge(List, low, mid, high);
            //打印出每次归并的区间
            cout << "low:" << low << " mid:" << mid << " high:" << high << endl;
            //下一次归并时第一序列的第一个元素位置
            low = high + 1;
        }// end of while
        //范围扩大一倍，二路归并的过程
        size *= 2;
    }// end of while
}

 

 

　　1.2.c++

递归

非递归

　　1.3.python

递归

非递归

def mergeSort(arr):
    import math
    if(len(arr)<2):
        return arr
    middle = math.floor(len(arr)/2)
    left, right = arr[0:middle], arr[middle:]
    return merge(mergeSort(left), mergeSort(right))

def merge(left,right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0));
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0));
    while right:
        result.append(right.pop(0));
    return result

 　　对路归并