论文总结
20179212 2017-2018-2 《密码与安全新技术》 论文总结
课程:《密码与安全新技术》
班级: 1792
姓名: 郭永健
学号: 20179212
上课教师:谢四江
必修/选修: 必修
一、题目讲解
Simple Proofs of Sequential Work------简单的连续工作证明
2018年欧密会最佳论文,作者:Krzysztof Pietrzak,密码学家、奥地利科学与技术学院研究员。Bram Cohen,BitTorrent创始人、Chia CEO
原文链接:https://eprint.iacr.org/2018/183.pdf
内容简介:
试图通过「空间证明」(Proof of Space)来保证比特币及其他加密货币的安全。「空间证明」是Bram Cohen之前提出的一种取代PoW的工作证明方式。
二、背景
- 工作量证明机制为比特币的网络提供了基本的安全性,但是这一验证机制却带来了巨大的资源浪费问题。BitTorrent创始人Bram Cohen在分布式系统领域声名远扬,他提出以计算机存储所有权验证作为工作量证明的替代方案,旨在结合空间证明与时间证明机制避免浪费问题。
- 虽然工作量证明(proof of work)为比特币网络提供了基本的安全性,但毫无疑问,使用其作为验证机制需要大量的电力。一旦拥有笔记本电脑的外行也可以挖掘区块,现在的挖矿过程所涉及的充满专门处理器的仓库,或多或少无用于除了比特币挖矿以外的任何目的。
- 即使忽略浪费的问题,电力密集型挖矿也不可避免地导致了该行业的地理分布趋于集中。由于矿工在电力更便宜的地方获得的回报最大,冰岛、中国西部地区及华盛顿州等地区已成为主要的中心地区。
- 为寻找一个能够激励与这些特性相反的系统(通用设备、非浪费的工作及低功耗),开发者Bram Cohen提出了计算机存储所有权验证作为工作量证明的替代方案。他提出的“空间证明(proof of space)”,认为这个建议是今天强化比特币这一概念需要使用的唯一其他资源就是存储。所以,结果就证实了空间证明在理论上的可能性,利用空间证明你便能够分配存储容量去来做这些事情。在空间证明系统下,矿工将一定量未使用的磁盘空间分配给网络,成功挖掘区块的概率与分配的空间量除以网络总容量成比例。的理念的自然迭代。
- 增加时间元素能够避免当空间证明是挖矿的唯一要求(就SpaceMint建议而言)时出现潜在漏洞。如果你只拥有空间证明,那么就存在一个问题:你要让挖矿不产生任何额外的花费。这就产生了一个固有问题,有些人拥有大量资源,自创建以来就可以不断重新挖矿——回到起点,创造一个全新的链条,然后将所有的奖励都给自己。
- 为了防止这种情况发生,使用时间证明结合空间证明,特别是从每个挖矿时期之间将流逝一段时间的专用时间服务器派生的证明。
- 尽管这一理念无法彻底消除自创建以来就存在的重新挖掘区块的能力,但这也意味着攻击者没有办法到达当前区块链。而他认为这一规定均被其他空间证明的建议所遗漏。
三、关键概念
工作量证明
简单理解就是一份证明,用来确认你做过一定量的工作。工作量证明系统主要特征是客户端需要做一定难度的工作得出一个结果,验证方却很容易通过结果来检查出客户端是不是做了相应的工作。这种方案的一个核心特征是不对称性:工作对于请求方是适中的,对于验证方则是易于验证的。
空间证明(proof-of-space)
依赖于磁盘空间而不是计算力作为挖矿的主要资源,创建了一种声称能够比PoW更加生态友好且经济的替代选择。这份标题为《以空间证明的应用超越赫尔曼的时间记忆折中》概述了通过使用空间证明(proof-of-space)建立一种对能源需求更少的挖矿流程——比特币的能源集约型挖矿模式一直遭受很多人的批评,被很多人认为是一种资源浪费。由于能源要求的降低,以及对现有硬件的依赖,这种方式旨在是任何拥有一台计算机的人都能够进行挖矿。在空间证明体系下,矿工可以将未使用的磁盘空间分配到网络中,而成功挖到区块的概率将与矿工分配的磁盘空间与网络的总能力成比例。
比特币中的工作量证明
工作量证明的算法可以大概描述为:在一个时间段同时有多台服务器对这一段时间的交易进行打包,打包完成后连带区块Header信息一起经过SHA256算法进行运算。在区块头以及奖励交易coinbase里各有一个变量nonce,如果运算的结果不符合难度要求,那么就调整nonce的值继续运算。如果有某台服务器率先计算出了符合难度值的区块,那么它可以广播这个区块。其他服务器验证没问题后就可以添加到现有区块链上,然后大家再一起竞争下一个区块。这个过程也称为挖矿。
比特币网络中任何一个节点,如果想生成一个新的区块并写入区块链,必须解出比特币网络出的工作量证明的迷题。这道题关键的三个要素是工作量证明函数、区块及难度值。工作量证明函数是这道题的计算方法,区块决定了这道题的输入数据,难度值决定了这道题的所需要的计算量。
区块
比特币的区块由区块头及该区块所包含的交易列表组成。区块头的大小为80字节,由4字节的版本号、32字节的上一个区块的散列值、32字节的Merkle Root Hash、4字节的时间缀(当前时间)、4字节的当前难度值、4字节的随机数组成。区块包含的交易列表则附加在区块头后面,其中的第一笔交易是coinbase交易,这是一笔为了让矿工获得奖励及手续费的特殊交易。
区块的大致结构如图所示:
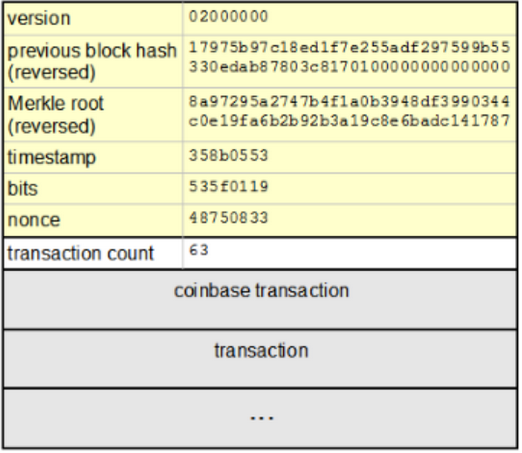
拥有80字节固定长度的区块头,就是用于比特币工作量证明的输入字符串。因此,为了使区块头能体现区块所包含的所有交易,在区块的构造过程中,需要将该区块要包含的交易列表,通过Merkle Tree算法生成Merkle Root Hash,并以此作为交易列表的摘要存到区块头中。其中Merkle Tree的算法图解如下:
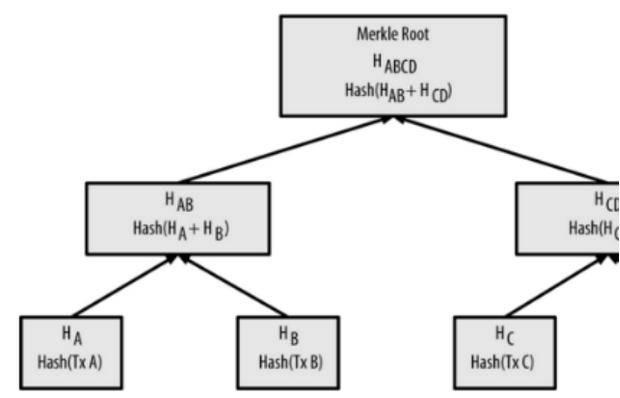
难度值
难度值(difficulty)是矿工们在挖矿时候的重要参考指标,它决定了矿工大约需要经过多少次哈希运算才能产生一个合法的区块。比特币的区块大约每10分钟生成一个,如果要在不同的全网算力条件下,新区块的产生保持都基本这个速率,难度值必须根据全网算力的变化进行调整。简单地说,难度值被设定在无论挖矿能力如何,新区块产生速率都保持在10分钟一个。
难度的调整是在每个完整节点中独立自动发生的。每2016个区块,所有节点都会按统一的公式自动调整难度,这个公式是由最新2016个区块的花费时长与期望时长(期望时长为20160分钟即两周,是按每10分钟一个区块的产生速率计算出的总时长)比较得出的,根据实际时长与期望时长的比值,进行相应调整(或变难或变易)。也就是说,如果区块产生的速率比10分钟快则增加难度,比10分钟慢则降低难度。
工作量证明的过程
我们可以把比特币矿工解这道工作量证明迷题的步骤大致归纳如下:
1、生成Coinbase交易,并与其他所有准备打包进区块的交易组成交易列表,通过Merkle Tree算法生成Merkle Root Hash
2、把Merkle Root Hash及其他相关字段组装成区块头,将区块头的80字节数据(Block Header)作为工作量证明的输入
3、不停的变更区块头中的随机数即nonce的数值,并对每次变更后的的区块头做双重SHA256运算(即SHA256(SHA256(Block_Header))),将结果值与当前网络的目标值做对比,如果小于目标值,则解题成功,工作量证明完成。
计算量分析
Hash值是由数字和大小写字母构成的字符串,每一位有62种可能性(可能为26个大写字母、26个小写字母,10个数字中任一个),假设任何一个字符出现的概率是均等的,那么第一位为0的概率是1/62(其他位出现什么字符先不管),理论上需要尝试62次Hash运算才会出现一次第一位为0的情况,如果前两2位为0,就得尝试62的平方次Hash运算,以n个0开头就需要尝试62的n次方次运算。
四、POSW
Publicly verifiable proofs of sequential work---公开可验证的公作证明
随机预言机(random oracle,简称RO)。在密码学里面,随机预言是一个预言(简单说像是理论的黑箱),对任何输入都回传一个真正均匀随机的输出(请参考离散型均匀分布),不过对相同的输入,该预言每次都会回传一模一样的输出。因为预言机实际上起到的是一个黑匣子的作用,中间是存在一个固定的算法的,这个算法相当复杂且是保密的,因此相同的输入值在经过了这个算法的运算之后输出的是相同的输出值,就像数学上一个确定的函数,相同的数值代入运算几次都会得到同样的结果一样。预言机存在的目的是为了让你无法知道自己的输入能得到什么样的结果,如果你给出两个输入,预言机同时给定两个输出的话,你不会知道这两个输出分别对应的是哪个输入。
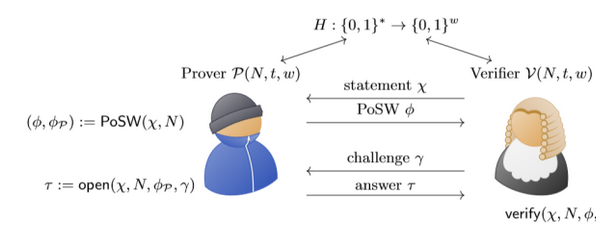
- N:时间参数 ,即 PoSW(χ,N) ,在收到w位的x 声明后N时间以及过去,计算得到φ。
- t是一个统计安全参数,较大的t的稳健性越好
- w是哈希函数的位数
- 公用输入P 和 V 获得相同的输入两个统计安全参数w, t 和时间参数N 。所有各方都可以访问随机 oracle H : {0,1}∗ → {0,1}w.
- 语句V 随机抽样χ ← {0,1}w 并将其发送到 P.
- 计算 PoSW P 计算 (理想情况下, 使N查询 H 顺序) 一个证明 (φ, φP): =PoSWH (χ, N)。P 将φ发送到 V 和本地存储φP.
- 打开挑战V 采样随机挑战γ ← {0,1}t·w 并将其发送到 P
- 打开P 计算τ : =打开H (χ、N、φP、γ) 并将其发送到 v.
- 验证V 计算和输出验证H (χ, N, φ, γ, τ) ∈ {接受,拒绝}.
我们需要完美正确性: 如果 V 与一个诚实的 P 交互, 那么它将输出接受以概率1。稳健属性要求任何潜在的恶意证明人 P , 如果以良好的概率进行 V 接受, 则必须按顺序查询H "几乎" N次数。即使在每一轮 Pe 都可以并行地在许多输入中查询 H, 而诚实 P 只需要使一个小 (在我们的构造1中, 在 [MMV13] 2 中) 每回合查询数.
总结
论文完成了一个连续工作的证明,它比[MMV13]中的原始结构更简单并且参数更好。 并对[MMV13]论文中提出的三个问题有了解答。
1、规划求解的空间复杂性。在我们构建时间戳和时间锁谜题的时候, 求解器保留 n 个顶点图的哈希标签。是否有其他使用 o (N) 存储的解决方案?或者有任何内在的原因, Ω (N) 存储是必要的?
论文中改进后的方案是空间复杂度以及降低至了O(logn)
2、深度稳健图的必要性。 我们构造的效率和安全性与深度文件图结构的参数密切相关:较低度的图给出了更多有效的解,而具有较高鲁棒性的图(在一些顶点之后剩余的最长路径的长度的下界是 移除)给我们带来较小对抗优势的谜题。 一个有趣的开放问题是逆向是否也持有:具有更好参数的时间锁定谜题还意味着存在具有更好参数的深度 - 稳健图表?
深度稳健图也不是必要的。只需要基础图就足以满足要求。
3、一个基于RO模型的POSW可以用于在诸如抛硬币之类的协议中实现公平。
这个问题还在研究中。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号